5. Teste de Welch
O Teste Welch é usado parar avaliar a significância entre a diferença das médias observadas.
Exemplo:
Considere um processo, produto ou serviço no qual queremos avaliar o impacto do fator A , tal que A tenha k níveis, sendo que esses níveis são fixos. Suponha que uma amostra de N unidades experimentais é selecionada de forma completamente aleatória de uma população de unidades experimentais. A unidade experimental é a unidade básica para o qual os tratamentos são aplicados.
| Fator | Resistencia |
|---|---|
| 15 | 7 |
| 15 | 7 |
| 15 | 15 |
| 15 | 11 |
| 15 | 9 |
| 20 | 12 |
| 20 | 17 |
| 20 | 12 |
| 20 | 18 |
| 20 | 18 |
| 25 | 14 |
| 25 | 18 |
| 25 | 18 |
| 25 | 19 |
| 25 | 19 |
| 30 | 19 |
| 30 | 25 |
| 30 | 22 |
| 30 | 19 |
| 30 | 23 |
| 35 | 7 |
| 35 | 10 |
| 35 | 11 |
| 35 | 15 |
| 35 | 11 |
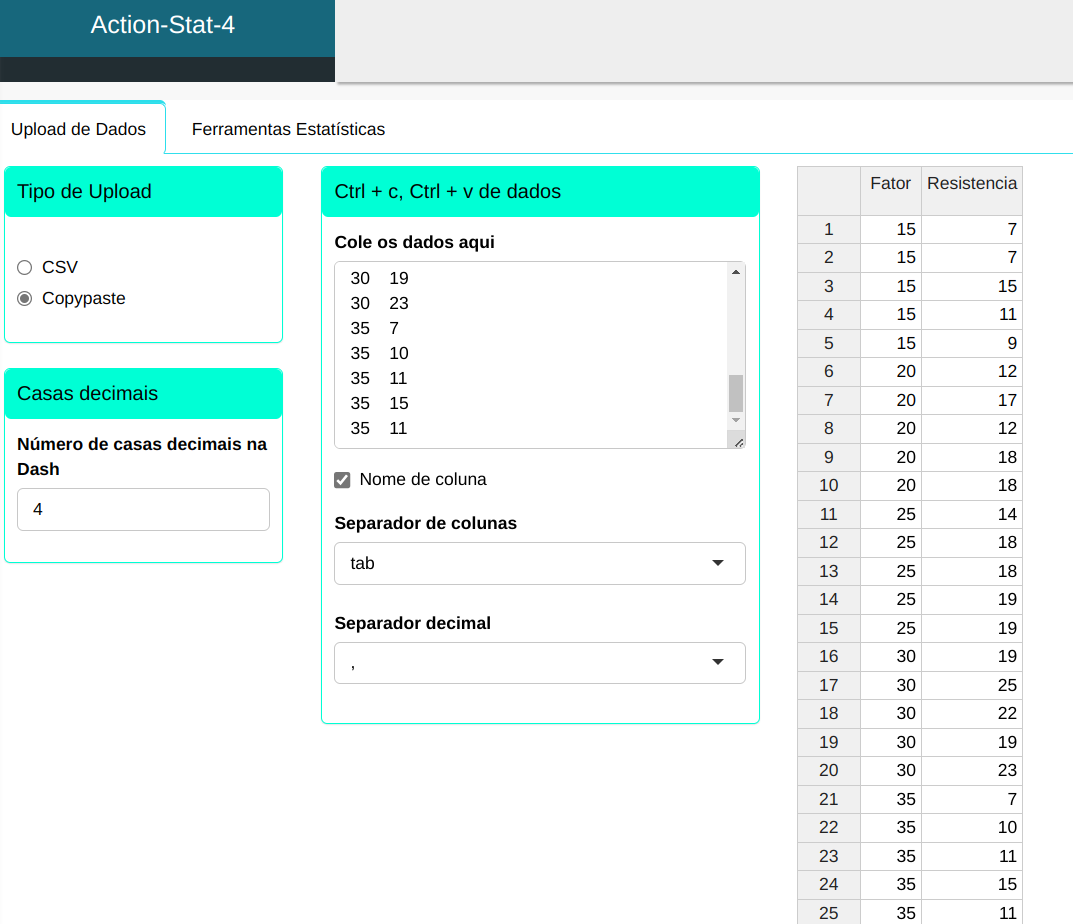
Faremos o teste de Welch:
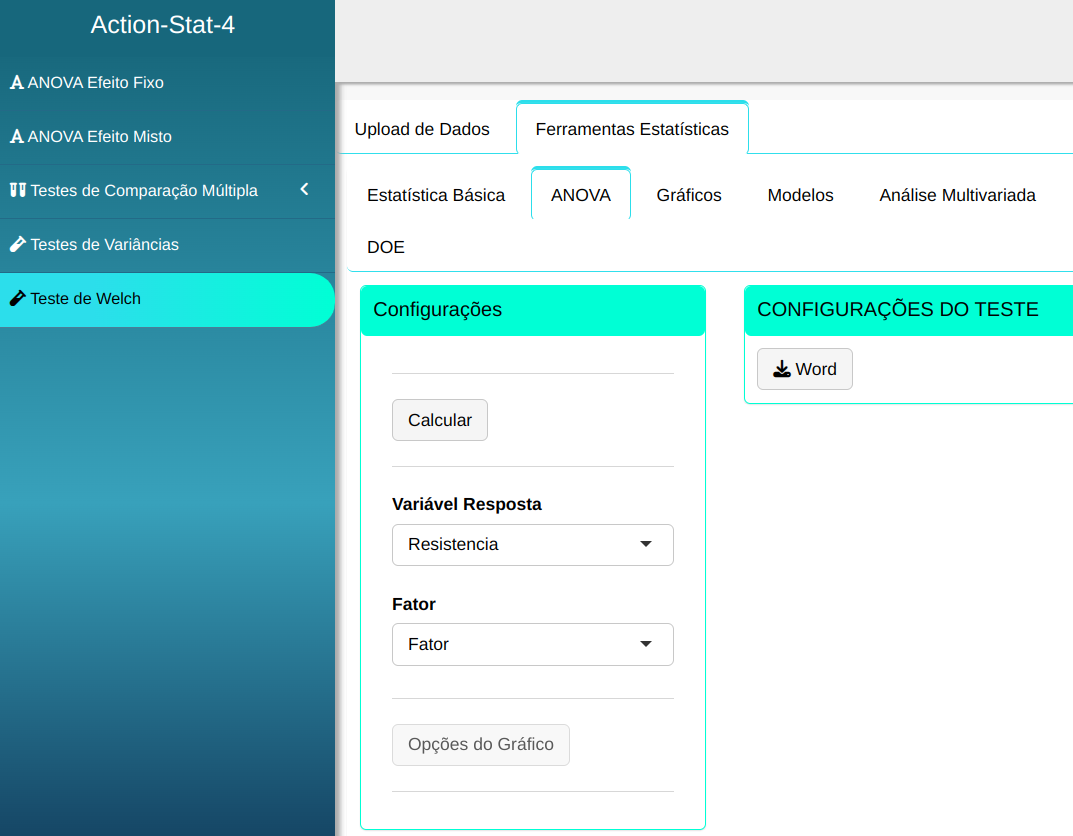
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Tabla 1: Teste de Welch (modelo heteroscedástico)
| Estat. F | GL Núm. | GL Denom | P-valor | |
|---|---|---|---|---|
| F | 12.451 | 4 | 9.916 | 0.000698745 |
Intervalo de Confiança das Médias
| Fator | Média | Desvio Padrão | Limite Inferior | Limite Superior |
|---|---|---|---|---|
| 15 | 9.8 | 3.347 | 5.645 | 13.955 |
| 20 | 15.4 | 3.130 | 11.513 | 19.287 |
| 25 | 17.6 | 2.074 | 15.025 | 20.175 |
| 30 | 21.6 | 2.608 | 18.362 | 24.838 |
| 35 | 10.8 | 2.864 | 7.244 | 14.356 |
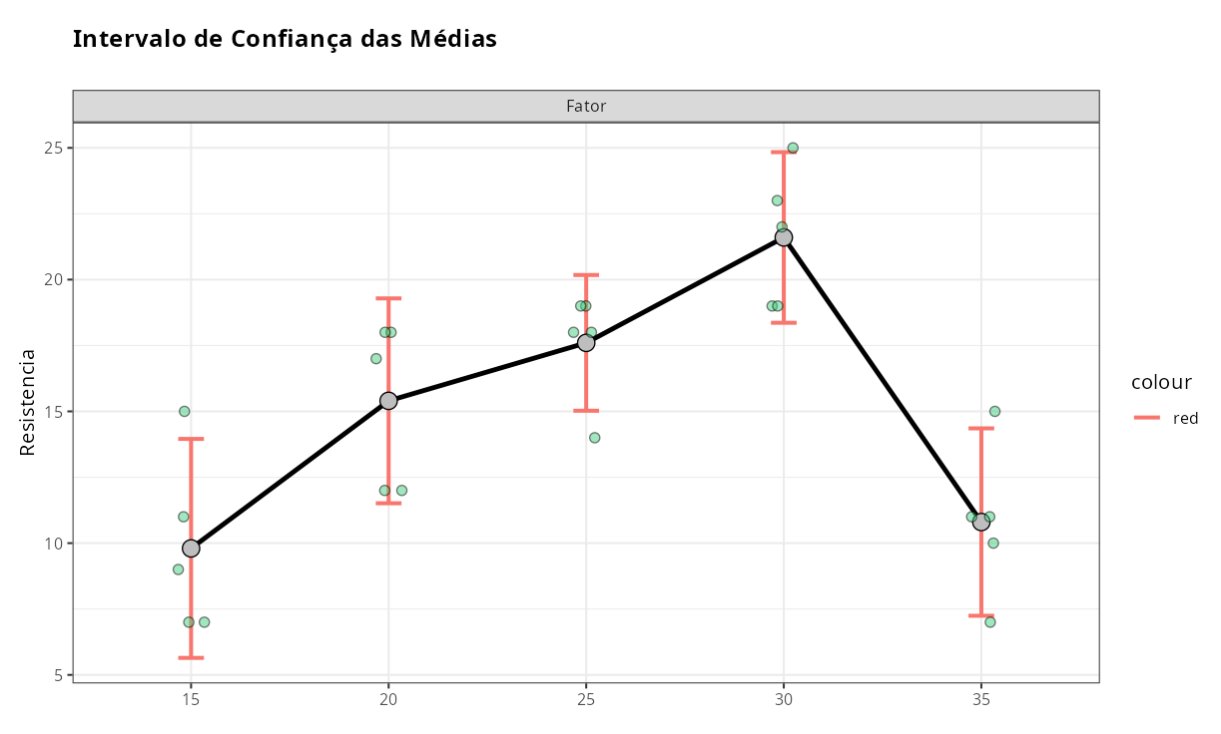
Como o p-valor = 0,000698745, rejeitamos a hipótese H0, isto é, para um nível de significância de 5% temos evidências de que as médias não são iguais. O gráfico acima, nos ajudam a chegar a essa conclusão.
No gráfico temos a média de cada nível e os respectivos intervalos de confiança.