3. Experimento com Replicas
Através deste manual analisamos experimentos com e sem réplicas.
Exemplo 1:
Estude o efeito ao longo do tempo de uma determinada reação química com a variação de temperatura e concentração de um reagente, conforme mostrado no diagrama abaixo.

| Variável de resposta | Y: Tempo de reação |
|---|---|
| Fatores | A: Concentração de Reagentes (Níveis $V_{-1}$=10% e $V_{+1}$=20%) |
| B: Temperatura (Níveis $T_{-1}$=80ºC e $T_{+1}$=90ºC) | |
| Tratamentos | $V_{-1}$ $T_{-1}$ - concentração a 10% e temperatura a 80ºC ((0)),$\quad$ & |
| $V_{+1}$ $T_{-1}$ - concentração em 20% e temperatura a 80ºC (a), | |
| $V_{-1}$ $T_{+1}$ - concentração em 10% e temperatura a 90ºC (b) | |
| $V_{+1}$ $T_{+1}$ - concentração em 20% e temperatura a 90ºC (ab) | |
| (O número de tratamentos é 2k, em este caso $2^2$=4) | |
| Unidade Experimental | Periodo de tempo para cada reação |
| Réplicas | Repetições do esperimento realizado nas mesmas condições |
| experimental, no caso do exemplo sob o mesmo nível de temperatura | |
| e reativo. Quanto mais réplicas, mais confiáveis os resultados do | |
| experimento. |
a) Obter as estimativas dos parâmetros do modelo;
b) Realizar testes de hipóteses para analisar a significância dos parâmetros.
Crie uma tabela conforme o modelo a seguir:
| Tratamento | A | B | Y |
|---|---|---|---|
| 0 | -1 | -1 | 26,6 |
| (a) | 1 | -1 | 40,9 |
| (b) | -1 | 1 | 11,8 |
| (ab) | 1 | 1 | 34 |
| 0 | -1 | -1 | 22 |
| (a) | 1 | -1 | 36,4 |
| (b) | -1 | 1 | 15,9 |
| (ab) | 1 | 1 | 29 |
| 0 | -1 | -1 | 22,8 |
| (a) | 1 | -1 | 36,7 |
| (b) | -1 | 1 | 14,3 |
| (ab) | 1 | 1 | 33,6 |
Primeiro, carregamos os dados, você pode inserir os dados no formato .csv ou copiando e colando os valores no campo.
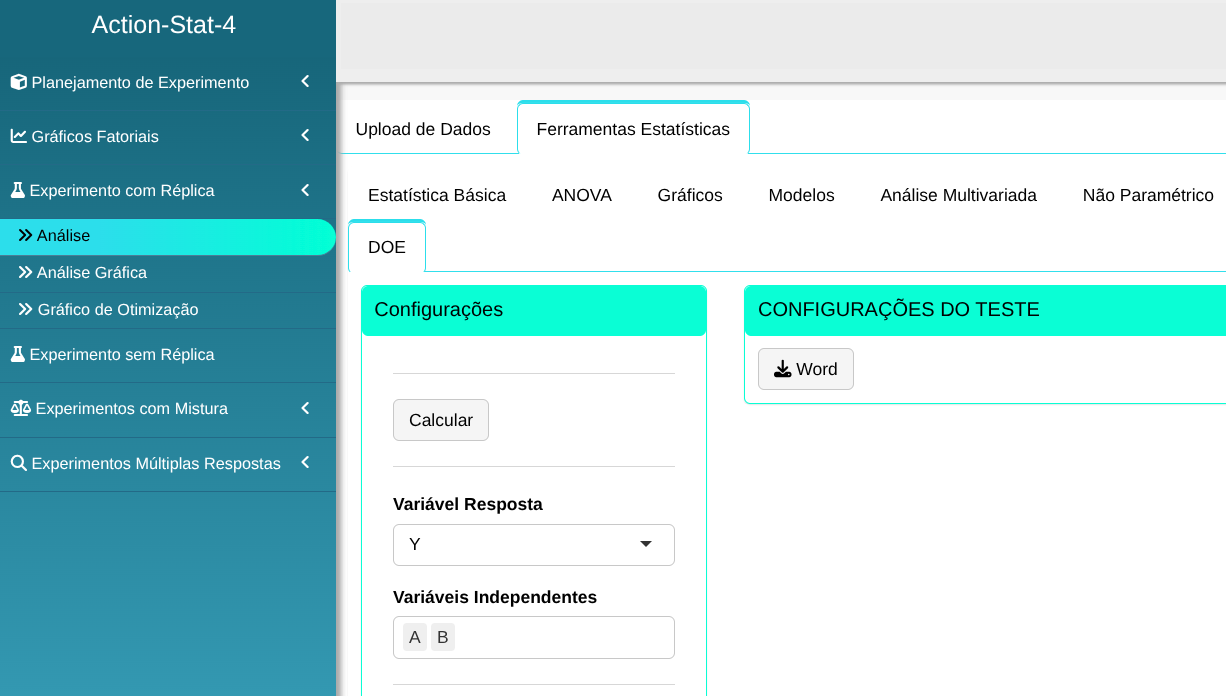
A análise do experimento será realizada conforme a configuração apresentada na figura abaixo.
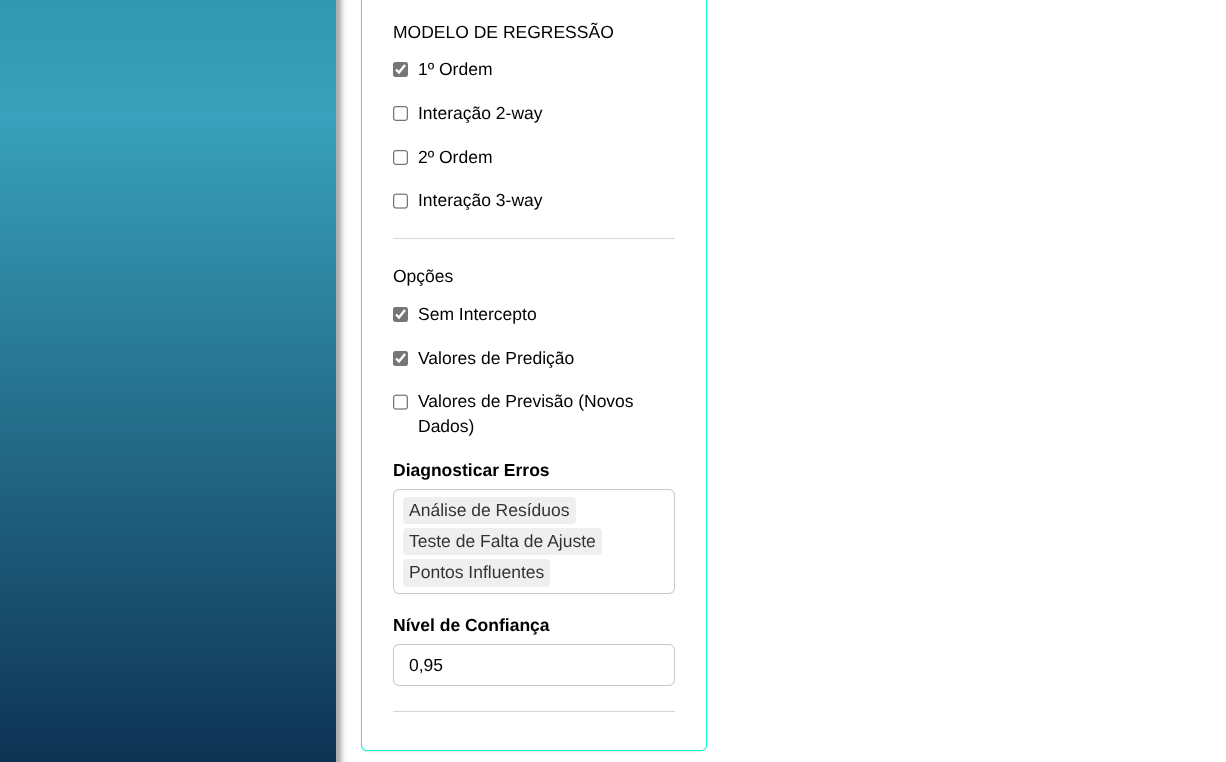
Ao clicar em Calcular, os resultados são exibidos. Um relatório desses resultados pode ser baixado em formato Word.

Os resultados são:
Tabela ANOVA
| GL | Soma dos Quadrados | Quadrado Médio | Estat. F | P Valor | |
|---|---|---|---|---|---|
| A | 1 | 787.32 | 787.320 | 0.894 | 0.367 |
| B | 1 | 182.52 | 182.520 | 0.207 | 0.659 |
| Resíduos | 10 | 8808.72 | 880.872 |
Análise Exploratória (resíduos)
| Mínimo | Q1 | Mediana | Média | Q3 | Máximo |
|---|---|---|---|---|---|
| 23.8 | 24.725 | 26.65 | 27 | 29.275 | 30.8 |
Coeficientes
| Efeitos | Estimativa | Desvio Padrão | Estat. t | P-valor | |
|---|---|---|---|---|---|
| A | 16.2 | 8.1 | 8.5677 | 0.9454 | 0.3667 |
| B | -7.8 | -3.9 | 8.5677 | -0.4552 | 0.6587 |
Medida descritiva da Qualidade do ajuste
| Desvio Padrão de Resíduos | Graus de Liberdade | R² | R² Ajustado |
|---|---|---|---|
| 29.6785 | 10 | 0.0992 | -0.081 |
Intervalo de confiança para os parâmetros
| 2.5% | 97.5% | |
|---|---|---|
| A | -10.9901 | 27.1901 |
| B | -22.9901 | 15.1901 |
Intervalo de Predição
| Y | A | B | Valor Ajustado | Limite inferior | Limite superior | Desvio Padrão | |
|---|---|---|---|---|---|---|---|
| 1 | 26.6 | -1 | -1 | -4.2 | -31.197 | 22.797 | 12.117 |
| 2 | 40.9 | 1 | -1 | 12 | -14.997 | 38.997 | 12.117 |
| 3 | 11.8 | -1 | 1 | -12 | -38.997 | 14.997 | 12.117 |
| 4 | 34 | 1 | 1 | 4.2 | -22.797 | 31.197 | 12.117 |
| 5 | 22 | -1 | -1 | -4.2 | -31.197 | 22.797 | 12.117 |
| 6 | 36.4 | 1 | -1 | 12 | -14.997 | 38.997 | 12.117 |
| 7 | 15.9 | -1 | 1 | -12 | -38.997 | 14.997 | 12.117 |
| 8 | 29 | 1 | 1 | 4.2 | -22.797 | 31.197 | 12.117 |
| 9 | 22.8 | -1 | -1 | -4.2 | -31.197 | 22.797 | 12.117 |
| 10 | 36.7 | 1 | -1 | 12 | -14.997 | 38.997 | 12.117 |
| 11 | 14.3 | -1 | 1 | -12 | -38.997 | 14.997 | 12.117 |
| 12 | 33.6 | 1 | 1 | 4.2 | -22.797 | 31.197 | 12.117 |
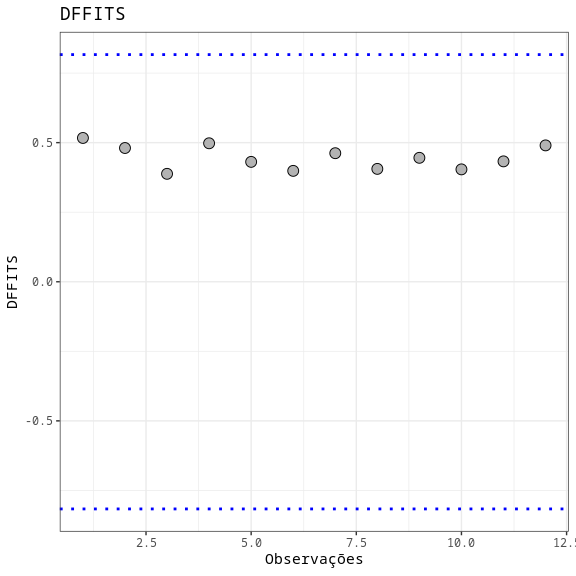
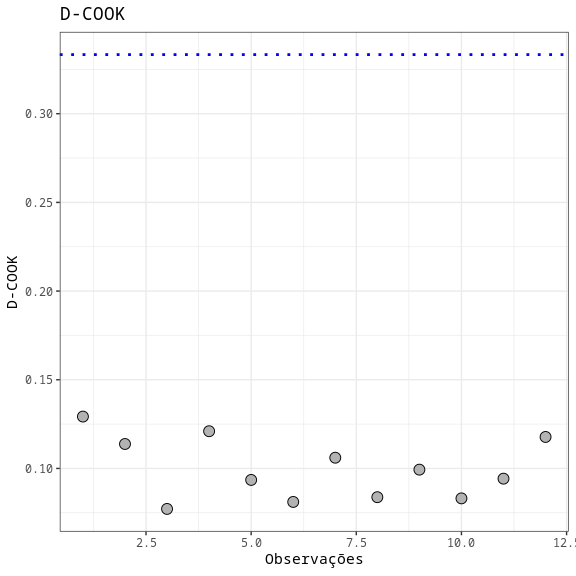
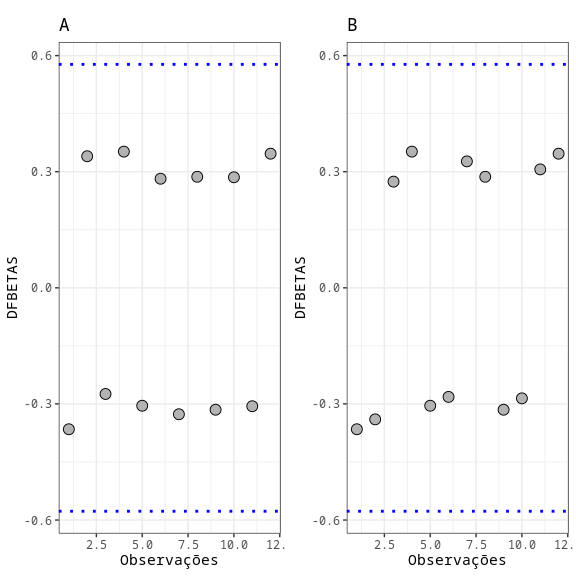
Resumo da Análise de Resíduos
| N.Obs | A | B | Resíduos | Resíduos Studentizados | Resíduos Padronizados | Leverage | DFFITS | DFBETA | D-COOK |
|---|---|---|---|---|---|---|---|---|---|
| 1 | -1 | -1 | 30.8 | 1.156 | 1.137 | 0.167 | 0.517 | -0.365 | 0.129 |
| 2 | 1 | -1 | 28.9 | 1.075 | 1.067 | 0.167 | 0.481 | -0.34 | 0.114 |
| 3 | -1 | 1 | 23.8 | 0.868 | 0.878 | 0.167 | 0.388 | 0.274 | 0.077 |
| 4 | 1 | 1 | 29.8 | 1.113 | 1.1 | 0.167 | 0.498 | 0.352 | 0.121 |
| 5 | -1 | -1 | 26.2 | 0.964 | 0.967 | 0.167 | 0.431 | -0.305 | 0.094 |
| 6 | 1 | -1 | 24.4 | 0.891 | 0.901 | 0.167 | 0.399 | -0.282 | 0.081 |
| 7 | -1 | 1 | 27.9 | 1.033 | 1.03 | 0.167 | 0.462 | 0.327 | 0.106 |
| 8 | 1 | 1 | 24.8 | 0.907 | 0.915 | 0.167 | 0.406 | 0.287 | 0.084 |
| 9 | -1 | -1 | 27 | 0.996 | 0.997 | 0.167 | 0.445 | -0.315 | 0.099 |
| 10 | 1 | -1 | 24.7 | 0.903 | 0.912 | 0.167 | 0.404 | -0.286 | 0.083 |
| 11 | -1 | 1 | 26.3 | 0.968 | 0.971 | 0.167 | 0.433 | 0.306 | 0.094 |
| 12 | 1 | 1 | 29.4 | 1.096 | 1.085 | 0.167 | 0.49 | 0.347 | 0.118 |
Critério
| Diagnóstico | Fórmula | Valor |
|---|---|---|
| hii (Leverage) | (2*(p+1))/n | 0.330 |
| DFFITS | 2* raiz ((p+1)/n) | 0.820 |
| DCOOK | 4/n | 0.333 |
| DFBETA | 2/raiz(n) | 0.580 |
| Resíduos Padronizados | (-3.3) | 3.000 |
| Resíduos Studentizados | (-3.3) | 3.000 |
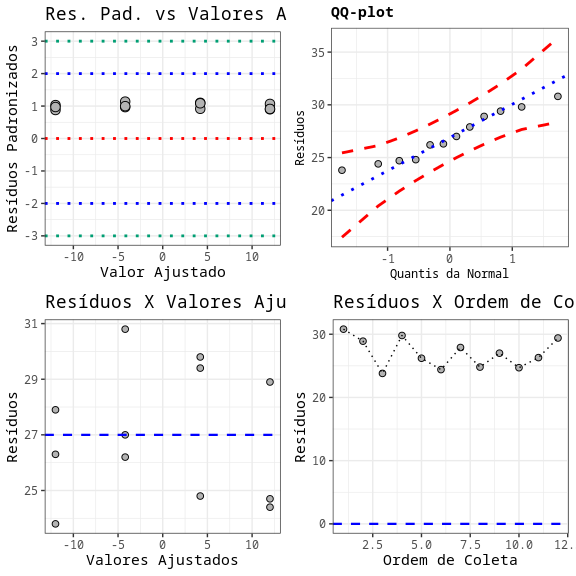
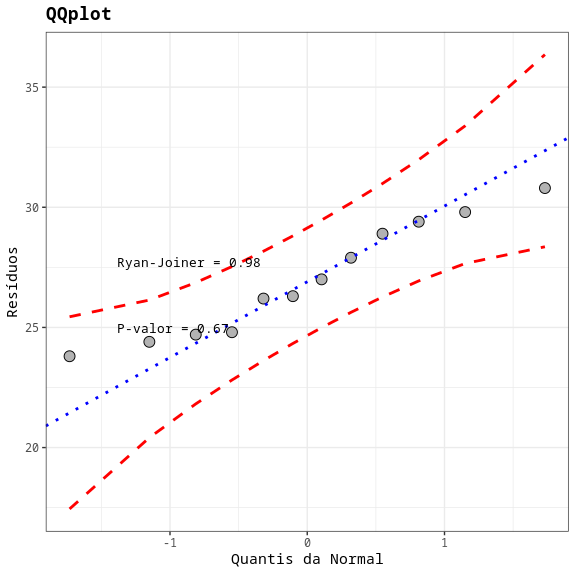
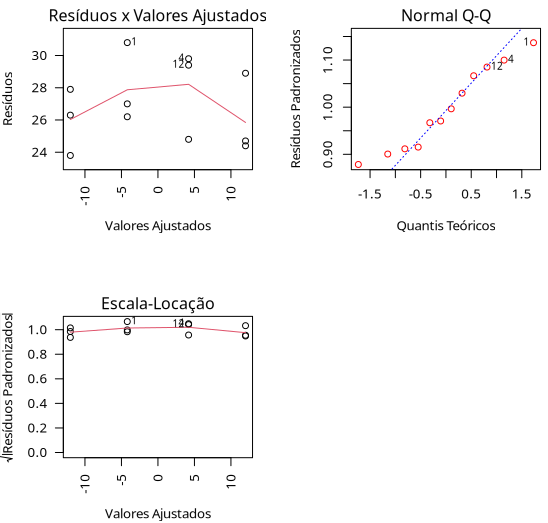
Teste de Normalidade
| Estatística | P-Valor | |
|---|---|---|
| Anderson-Querido | 0.290 | 0.549 |
| Shapiro-Wilk | 0.941 | 0.515 |
| Kolmogorov-Smirnov | 0.159 | 0.552 |
| Ryan-Joiner | 0.979 | 0.669 |
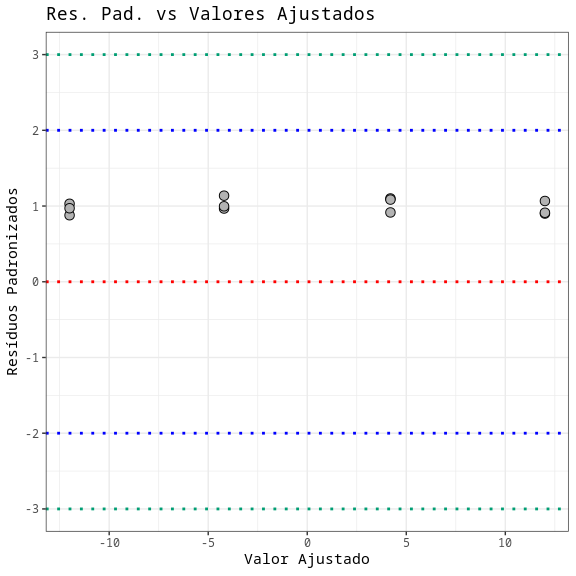
Teste de Homocedasticidade - Breusch Pagan
| Estatística | GL | P-valor |
|---|---|---|
| 0 | 1 | 0.9999 |
Teste de Homocedasticidade - Goldfeld Quandt
| Variável | Estatística | GL1 | GL2 | P-valor |
|---|---|---|---|---|
| A | 0.543762619611975 | 3 | 2 | 0.602191866042602 |
| B | 0.538356274651855 | 3 | 2 | 0.597230105553078 |
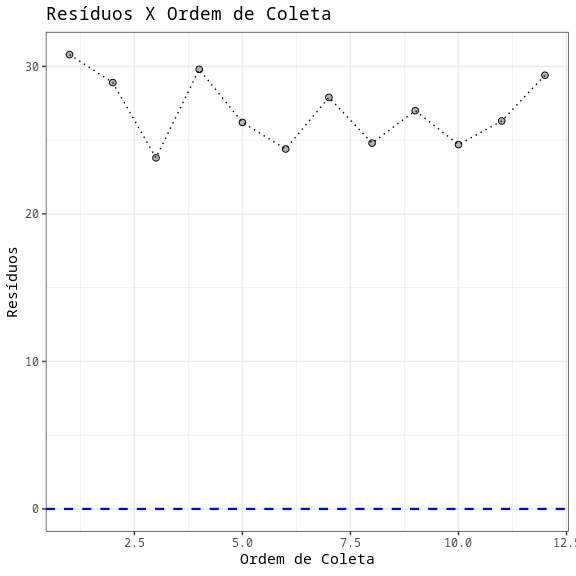
Teste de Independência - Durbin-Watson
| Estatística | P-valor |
|---|---|
| 0.0143 | 0 |
Teste de Falta de Ajuste
| GL | Soma de Quadrados | Quadrado Médio | Estat. F | P-valor | |
|---|---|---|---|---|---|
| A | 1 | 787.32 | 787.320 | 129.281 | 0.000 |
| B | 1 | 182.52 | 182.520 | 29.970 | 0.001 |
| Resíduos | 10 | 8808.72 | 880.872 | ||
| Falta de Ajuste | 2 | 8760.00 | 4380.000 | 719.212 | 0.000 |
| Erro Puro | 8 | 48.72 | 6.090 |
Resultado da análise
| Y | A | B |
|---|---|---|
| 26.6 | -1 | -1 |
| 40.9 | 1 | -1 |
| 11.8 | -1 | 1 |
| 34.0 | 1 | 1 |
| 22.0 | -1 | -1 |
| 36.4 | 1 | -1 |
| 15.9 | -1 | 1 |
| 29.0 | 1 | 1 |
| 22.8 | -1 | -1 |
| 36.7 | 1 | -1 |
| 14.3 | -1 | 1 |
| 33.6 | 1 | 1 |
O valor de 0,025; 12-3-1=2,306 e assim concluímos que, com nível $\alpha$ = 5%, os fatores A e B são significativos e a interação AB não é significativa. Basta ver que os coeficientes de regressão de A e B são respectivamente +1 e -1 e como estamos interessados em obter a menor resposta (menor tempo de reação), escolhemos os níveis A-B+.
Com os resultados obtidos podemos realizar uma análise gráfica no sistema de obtenção ou gráfico de contorno e superfície.
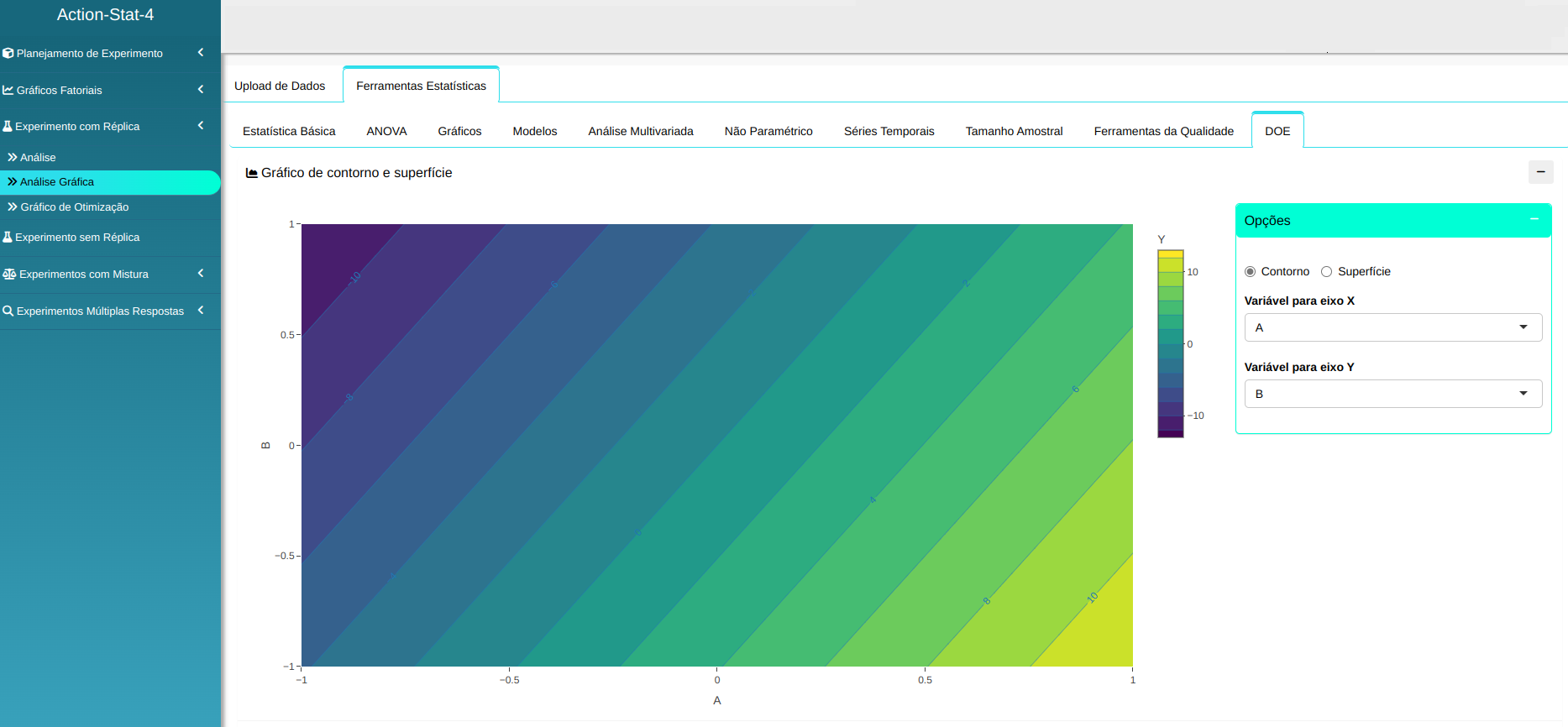
Na mesma página, você pode construir um gráfico da região factível escolhendo o limite superior e inferior da resposta

Além disso, é possível construir a tabela de otimização.
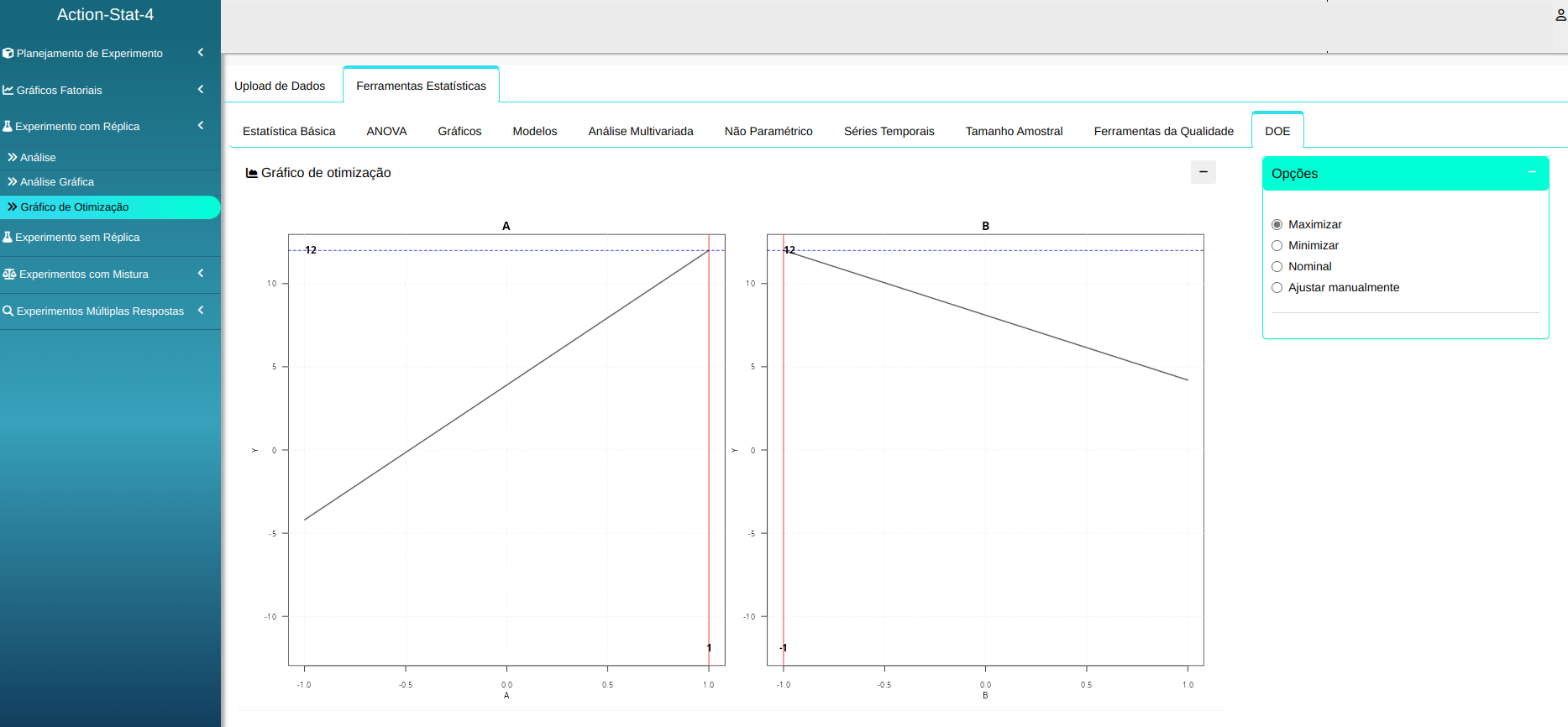
Exemplo 2:
Um determinado produto químico é produzido em um recipiente de pressão. Com o objetivo de estudar quais fatores influenciam a taxa de filtração de produto (Y), foi realizado um experimento fatorial no qual foram considerados 4 fatores: A (temperatura), B (pressão), C (concentração de formaldeído) e D (velocidade de agitação), Cada fator é observado em dois níveis.
| Tratamento | A | B | C | D | Y |
|---|---|---|---|---|---|
| 0 | -1 | -1 | -1 | -1 | 45 |
| a | 1 | -1 | -1 | -1 | 71 |
| b | -1 | 1 | -1 | -1 | 48 |
| ab | 1 | 1 | -1 | -1 | 65 |
| c | -1 | -1 | 1 | -1 | 68 |
| ac | 1 | -1 | 1 | -1 | 60 |
| bc | -1 | 1 | 1 | -1 | 80 |
| abc | 1 | 1 | 1 | -1 | 65 |
| d | -1 | -1 | -1 | 1 | 43 |
| ad | 1 | -1 | -1 | 1 | 100 |
| bd | -1 | 1 | -1 | 1 | 45 |
| abd | 1 | 1 | -1 | 1 | 104 |
| cd | -1 | -1 | 1 | 1 | 75 |
| acd | 1 | -1 | 1 | 1 | 86 |
| bcd | -1 | 1 | 1 | 1 | 70 |
| abcd | 1 | 1 | 1 | 1 | 96 |
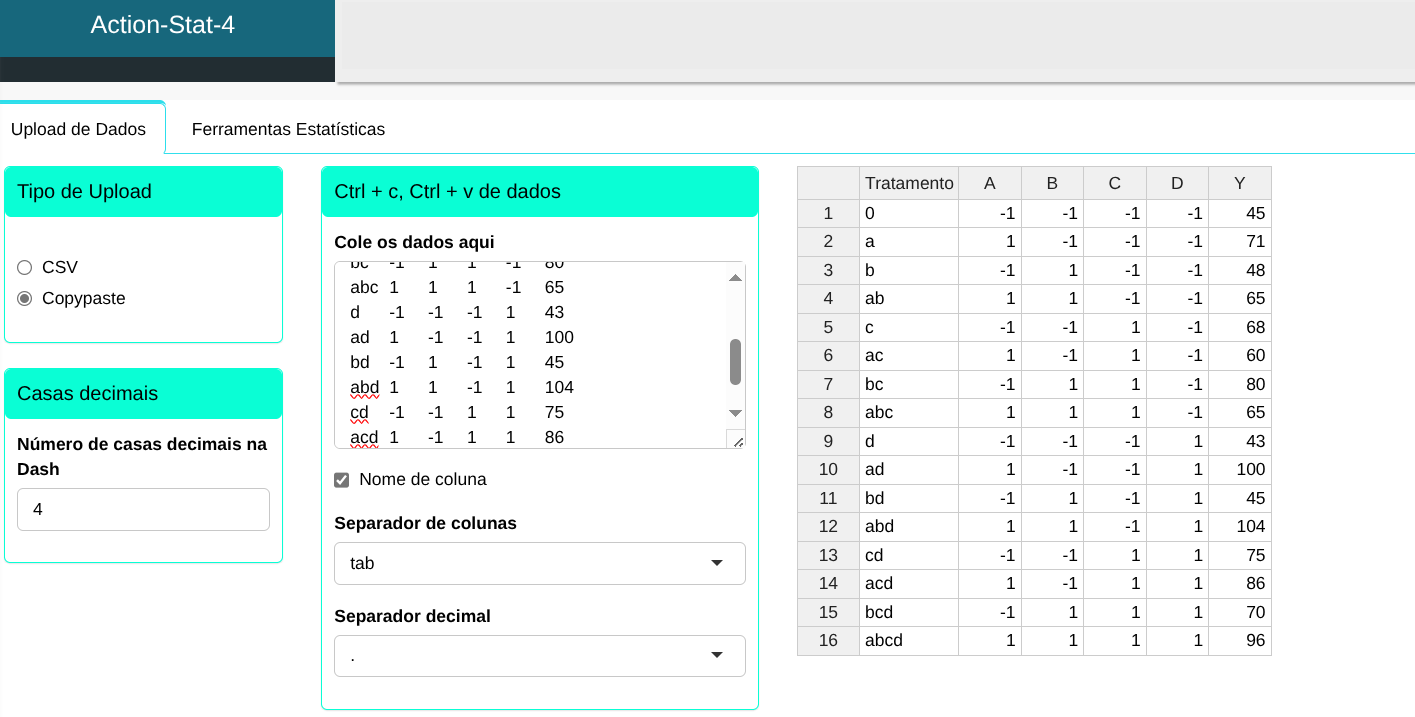
Faremos a análise do experimento
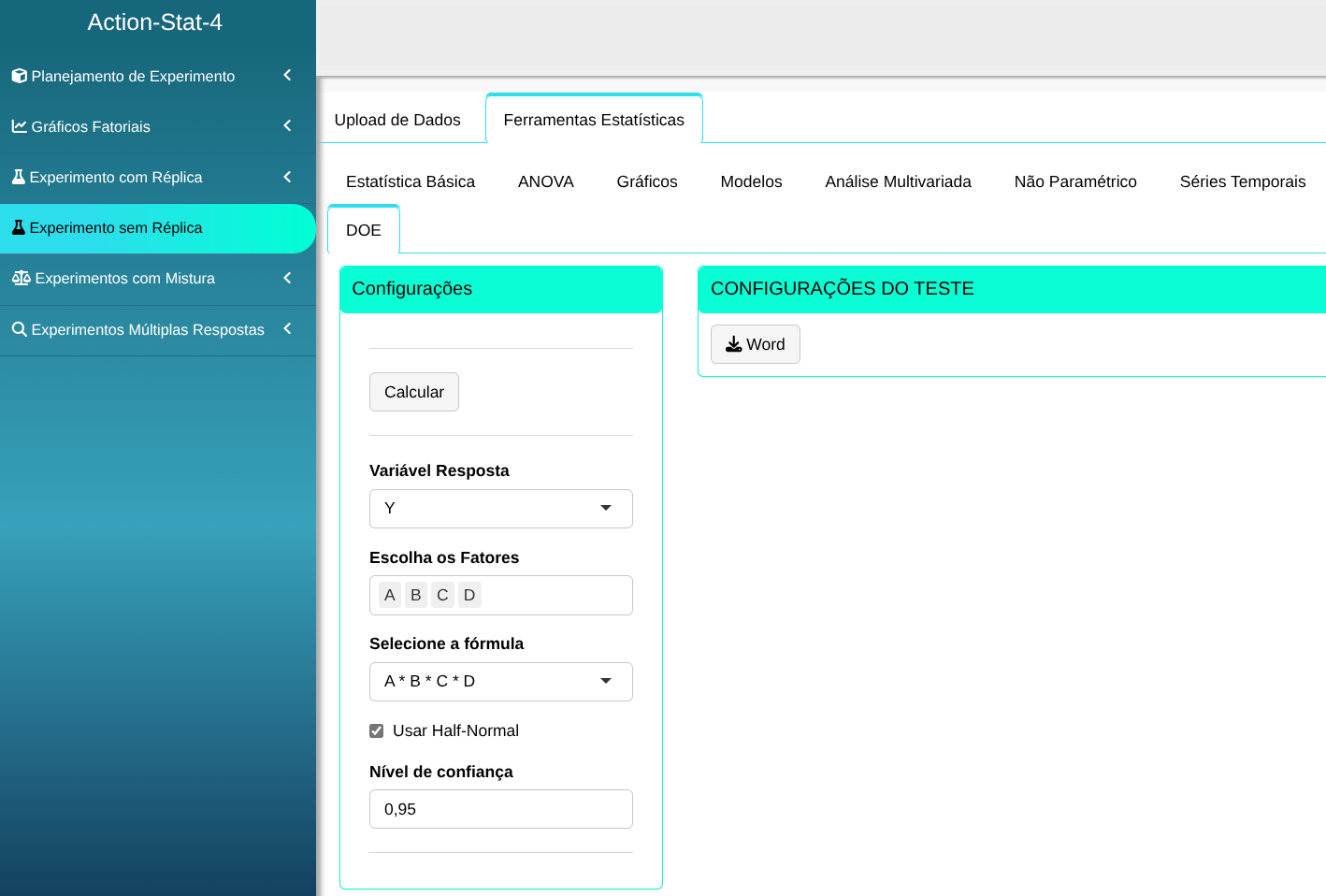
Ao clicar em calcular obtemos os resultados
Os resultados são:
Análise de experimentos sem Réplica
| Efeitos | Estimativa | Limite inferior | Limite superior | Estatística t | P-valor | |
|---|---|---|---|---|---|---|
| Intercepto | 70.0625 | |||||
| A | 21.6250 | 10.8125 | 14.8772 | 28.3728 | 8.2381 | 0.0004 |
| B | 3.1250 | 1.5625 | -3.6228 | 9.8728 | 1.1905 | 0.2873 |
| C | 9.8750 | 4.9375 | 3.1272 | 16.6228 | 3.7619 | 0.0131 |
| D | 14.6250 | 7.3125 | 7.8772 | 21.3728 | 5.5714 | 0.0026 |
| A:B | 0.1250 | 0.0625 | -6.6228 | 6.8728 | 0.0476 | 0.9639 |
| A:C | -18.1250 | -9.0625 | -24.8728 | -11.3772 | 6.9048 | 0.0010 |
| B:C | 2.3750 | 1.1875 | -4.3728 | 9.1228 | 0.9048 | 0.4071 |
| A:D | 16.6250 | 8.3125 | 9.8772 | 23.3728 | 6.3333 | 0.0014 |
| B:D | -0.3750 | -0.1875 | -7.1228 | 6.3728 | 0.1429 | 0.8920 |
| C:D | -1.1250 | -0.5625 | -7.8728 | 5.6228 | 0.4286 | 0.6861 |
| A:B:C | 1.8750 | 0.9375 | -4.8728 | 8.6228 | 0.7143 | 0.5070 |
| A:B:D | 4.1250 | 2.0625 | -2.6228 | 10.8728 | 1.5714 | 0.1769 |
| A:C:D | -1.6250 | -0.8125 | -8.3728 | 5.1228 | 0.6190 | 0.5630 |
| B:C:D | -2.6250 | -1.3125 | -9.3728 | 4.1228 | 1.0000 | 0.3632 |
| A:B:C:D | 1.3750 | 0.6875 | -5.3728 | 8.1228 | 0.5238 | 0.6228 |
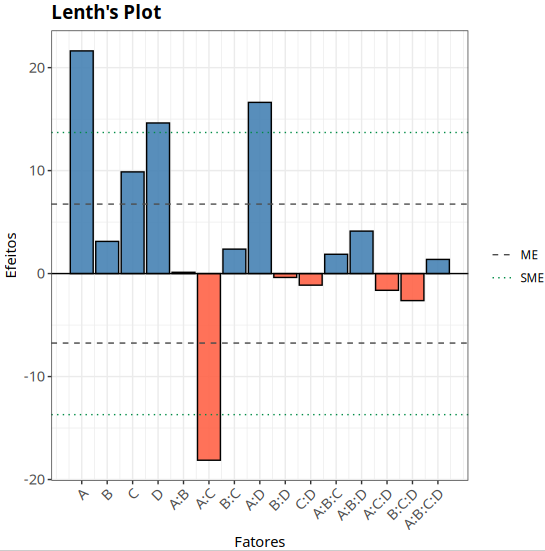
Análise de Experimentos sem Réplicas
| alfa | PSE | ME | SME | t.crít |
|---|---|---|---|---|
| 0.0500 | 2.6250 | 6.7478 | 13.6990 | 2.5706 |
Análise de Experimentos sem Réplicas
| Efeitos em Módulo | Half-normal score | |
|---|---|---|
| A | 21.6250 | 2.1280 |
| B | 3.1250 | 0.7835 |
| C | 9.8750 | 1.0364 |
| D | 14.6250 | 1.1918 |
| A:B | 0.1250 | 0.0418 |
| A:C | 18.1250 | 1.6449 |
| B:C | 2.3750 | 0.5730 |
| A:D | 16.6250 | 1.3830 |
| B:D | 0.3750 | 0.1257 |
| C:D | 1.1250 | 0.2104 |
| A:B:C | 1.8750 | 0.4770 |
| A:B:D | 4.1250 | 0.9027 |
| A:C:D | 1.6250 | 0.3853 |
| B:C:D | 2.6250 | 0.6745 |
| A:B:C:D | 1.3750 | 0.2967 |
Daniel Plot
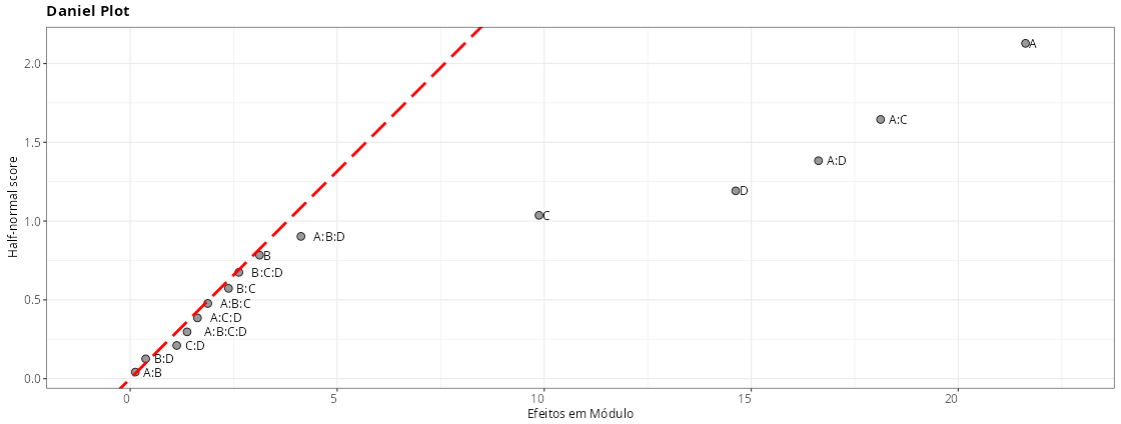
A partir dos resultados e gráficos obtidos. temos que para os fatores A. D e interações A:C e A:D são significativos.