6. Experimento Multiplas Respostas
Esta ferramenta do Action permite realizar um Experimento com Múltiplas variáveis e Múltiplas respostas, podendo realizar gráficos interativos.
Exemplo:
Realizaremos a análise com a seguinte base de dados:
| x1 |
x2 |
y1 |
y2 |
y3 |
| -1 |
-1 |
76.5 |
62 |
2940 |
| -1 |
1 |
77.0 |
60 |
3470 |
| 1 |
-1 |
78.0 |
66 |
3680 |
| 1 |
1 |
79.5 |
59 |
3890 |
| 0 |
0 |
79.9 |
72 |
3480 |
| 0 |
0 |
80.3 |
69 |
3200 |
| 0 |
0 |
80.0 |
68 |
3410 |
| 0 |
0 |
79.7 |
70 |
3290 |
| 0 |
0 |
79.8 |
71 |
3500 |
| 1414 |
0 |
78.4 |
68 |
3360 |
| -1414 |
0 |
75.6 |
71 |
3020 |
| 0 |
1414 |
78.5 |
58 |
3630 |
| 0 |
-1414 |
77.0 |
57 |
3150 |
Faremos o upload dos dados no sistema.
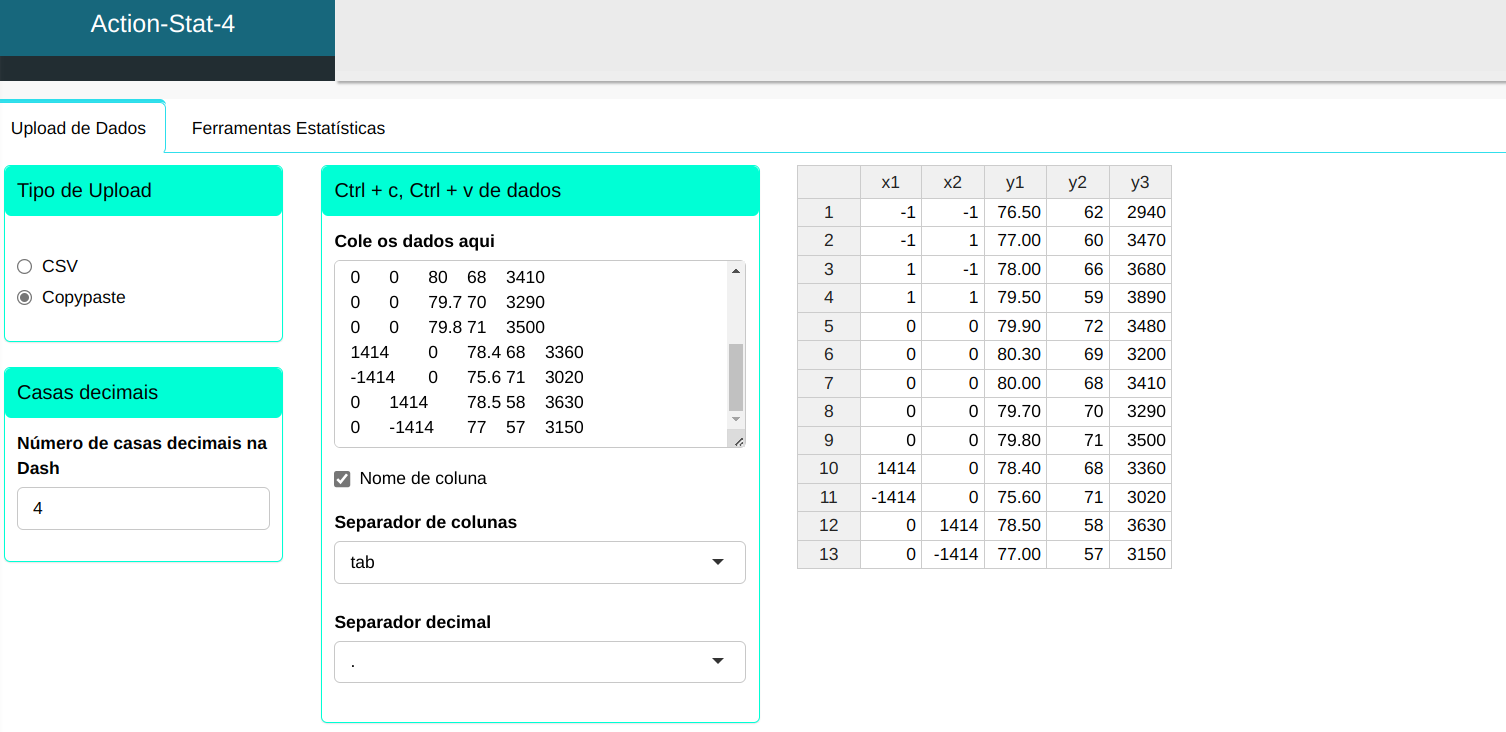
Para realizar a análise, basta aceder DOE e selecionar as opções conforme a figura abaixo.
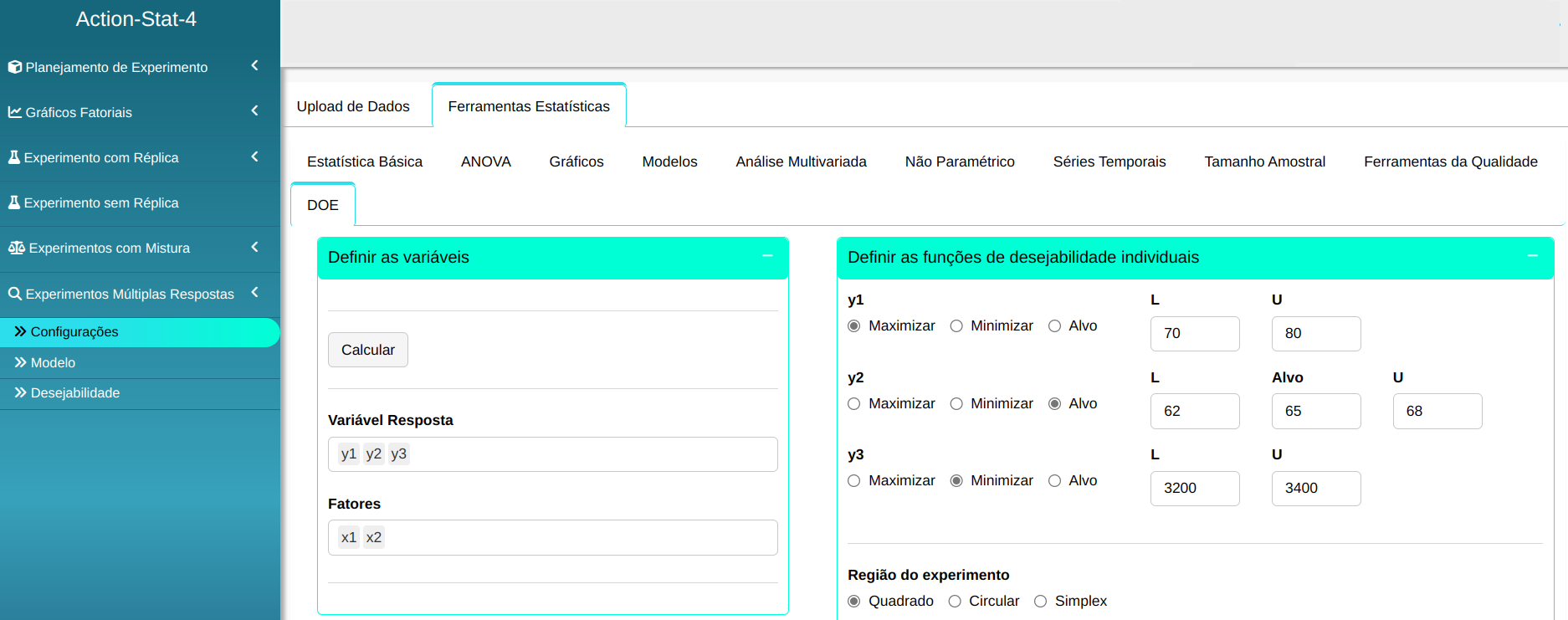

Clicando em Calcular, poderemos observar os resultados na aba “Modelos”.
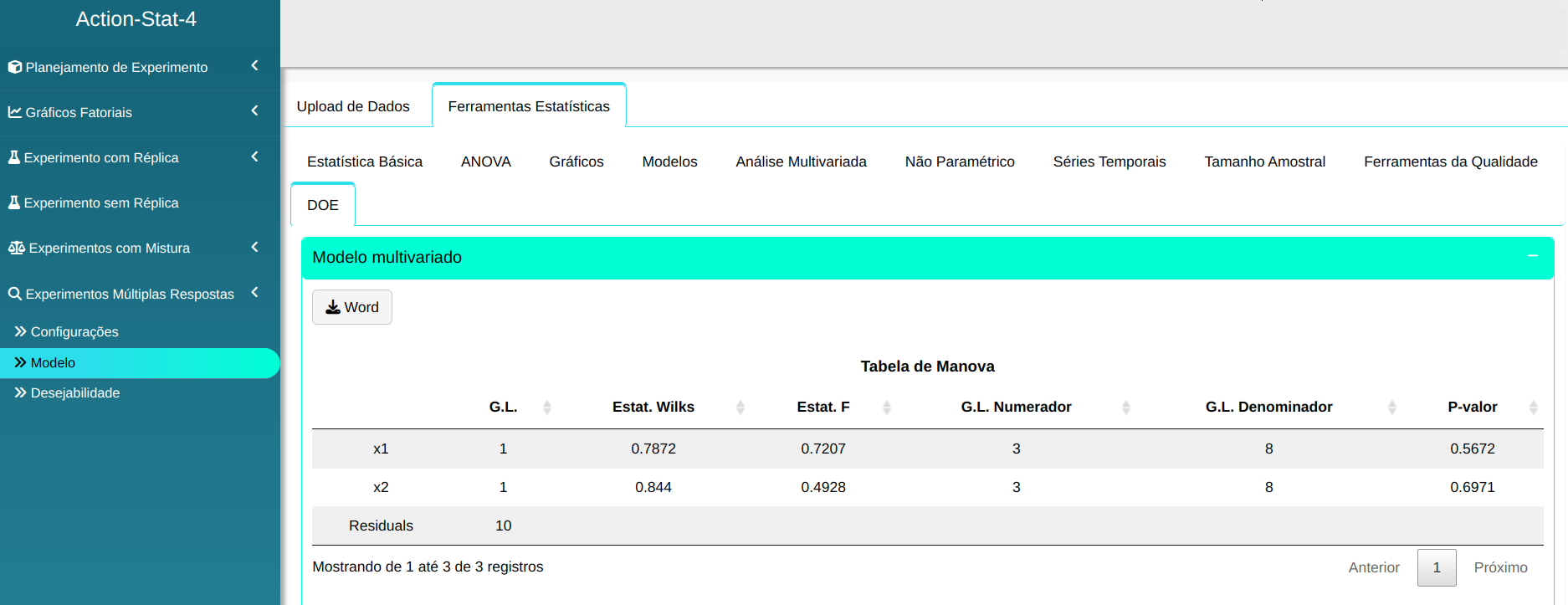


Os resultados são:
Tabela de Manova
|
G.L. |
Estat. Wilks |
Estat. F |
G.L. Numerador |
G.L. Denominador |
P-valor |
| x1 |
1 |
0.7872343 |
0.7207196 |
3 |
8 |
0.5671869 |
| x2 |
1 |
0.8440357 |
0.4927573 |
3 |
8 |
0.6971357 |
| Residuals |
10 |
|
|
|
|
|
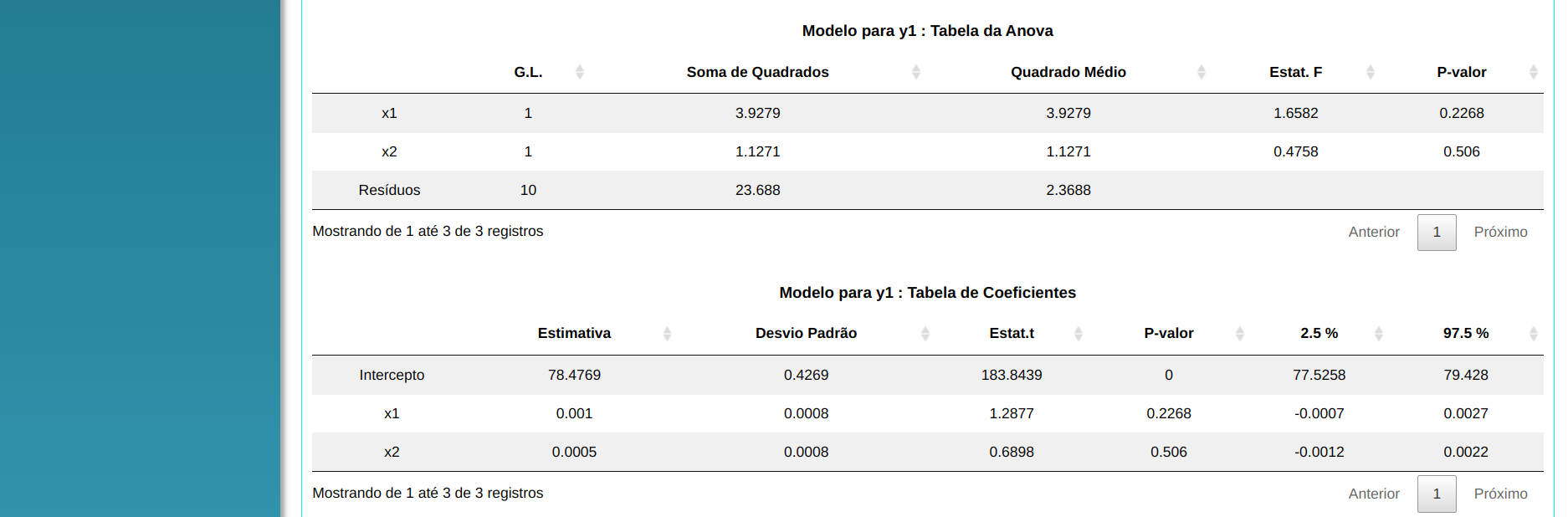
Modelo para y1 : Tabela da Anova
|
G.L. |
Soma de Quadrados |
Quadrado Médio |
Estat. F |
P-valor |
| x1 |
1 |
3.927921 |
3.927921 |
1.6581877 |
0.2268496 |
| x2 |
1 |
1.127122 |
1.127122 |
0.4758189 |
0.5060141 |
| Resíduos |
10 |
23.688035 |
2.368803 |
|
|
Modelo para y1 : Tabela de Coeficientes
|
Estimativa |
Desvio Padrão |
Estat. t |
P-valor |
2.5% |
97.5% |
| Intercepto |
78.4769 |
0.4269 |
183.8439 |
0 |
77.5258 |
79.428 |
| x1 |
0.001 |
0.0008 |
1.2877 |
0.2268 |
-0.0007 |
0.0027 |
| x2 |
0.0005 |
0.0008 |
0.6898 |
0.506 |
-0.0012 |
0.0022 |
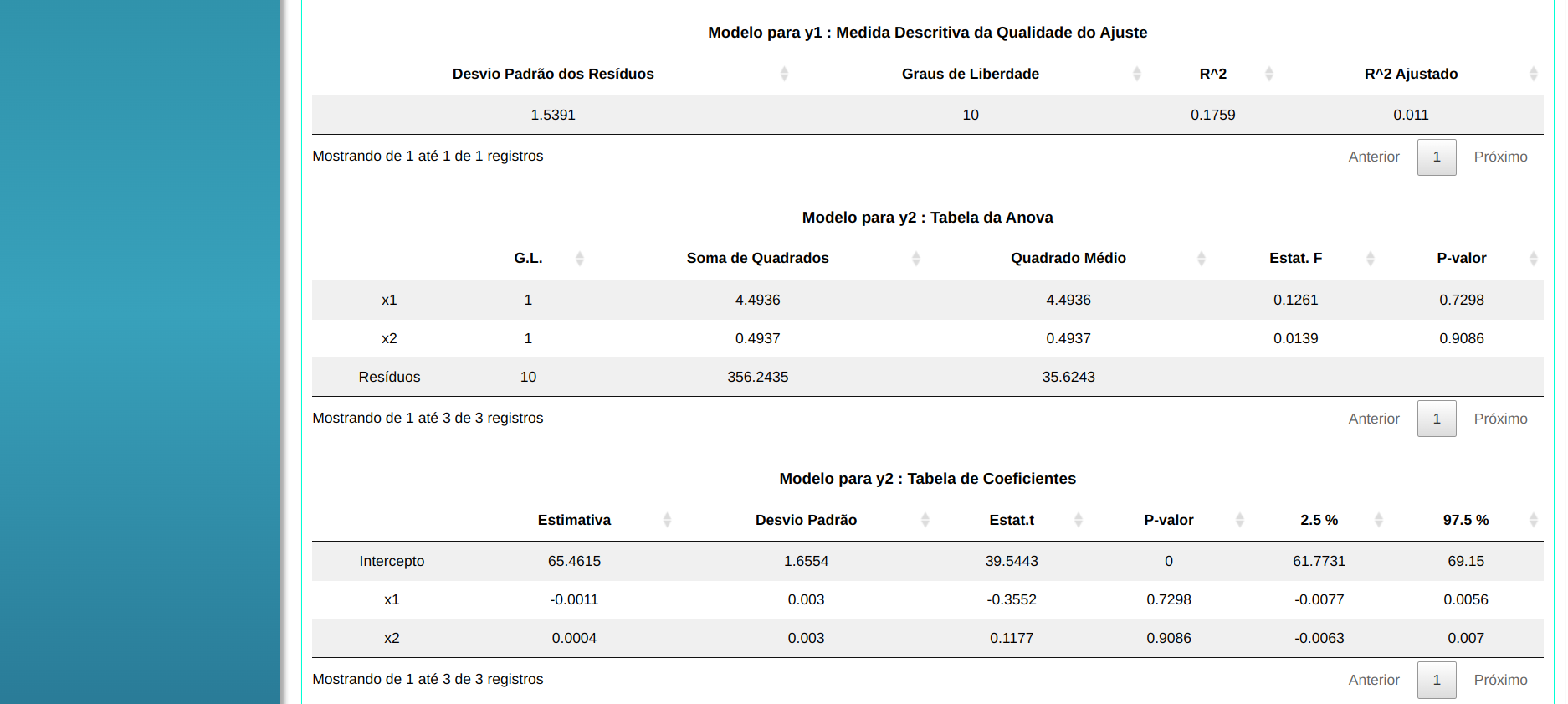
Modelo para y1 : Medida Descritiva da Qualidade do Ajuste
| Desvio Padrão dos Resíduos |
Graus de Liberdade |
R² |
R² Ajustado |
| 1.539092 |
10 |
0.175869 |
0.01104389 |
Modelo para y2 : Tabela da Anova
| — |
G.L. |
Soma de Quadrados |
Quadrado Médio |
Estat. F |
P-valor |
| x1 |
1 |
4.4936328 |
4.4936328 |
0.12613937 |
0.7298457 |
| x2 |
1 |
0.4936548 |
0.4936548 |
0.01385723 |
0.9086230 |
| Resíduos |
10 |
356.2434816 |
35.6243482 |
|
|
Modelo para y2 : Tabela de Coeficientes
|
Estimativa |
Desvio Padrão |
Estat. t |
P-valor |
2.5% |
97.5% |
| Intercepto |
65.4615 |
1.6554 |
39.5443 |
0 |
61.7731 |
69.15 |
| x1 |
-0.0011 |
0.003 |
-0.3552 |
0.7298 |
-0.0077 |
0.0056 |
| x2 |
0.0004 |
0.003 |
0.1177 |
0.9086 |
-0.0063 |
0.007 |
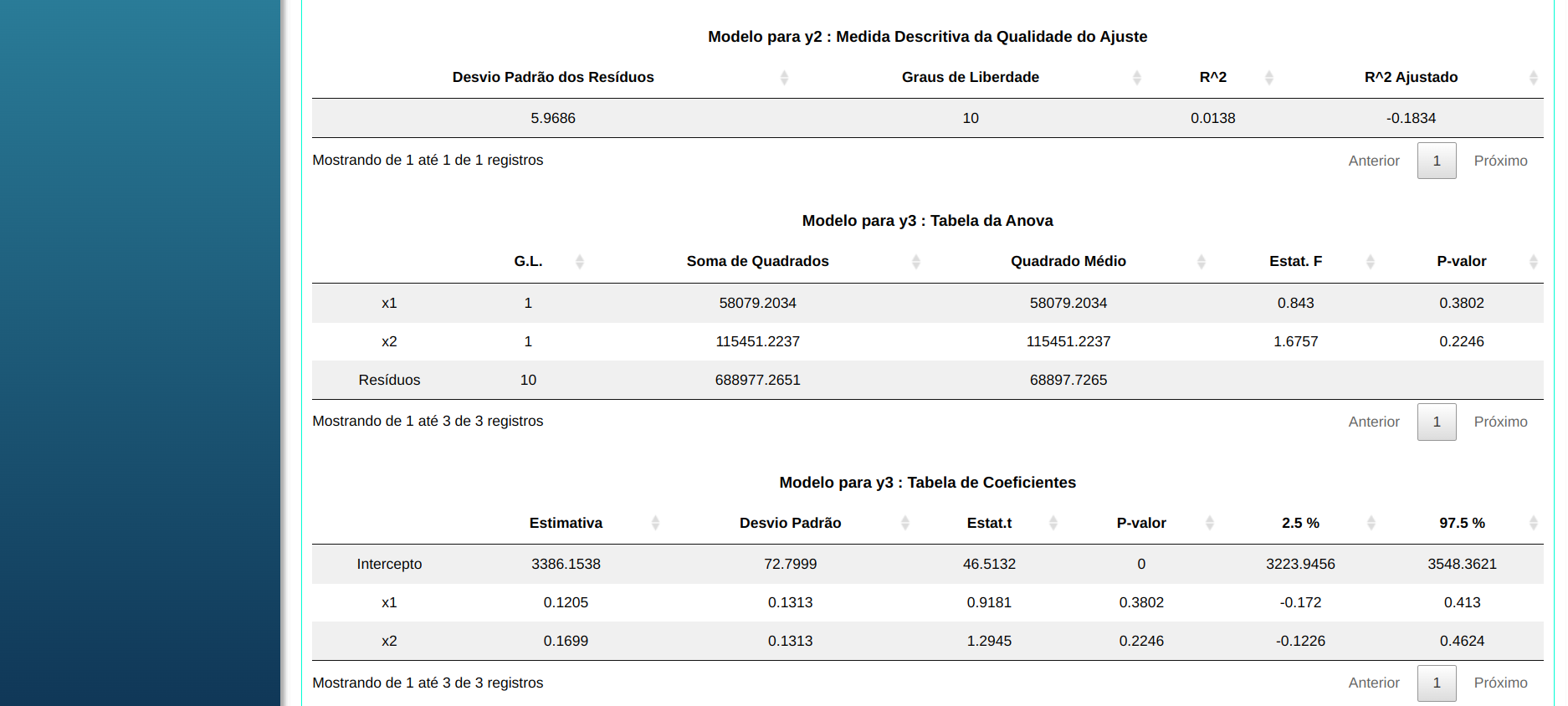
Modelo para y2: Medida Descritiva da Qualidade do Ajuste
| Desvio Padrão dos Resíduos |
Graus de Liberdade |
$R^2$ |
$R^2$ Ajustado |
| 5.968614 |
10 |
0.0138063 |
-0.1834323 |
Modelo para y3 : Tabela da Anova
|
G.L. |
Soma de Quadrados |
Quadrado Médio |
Estat. F |
P-valor |
| x1 |
1 |
58079.2 |
58079.20 |
0.8429771 |
0.3801587 |
| x2 |
1 |
115451.2 |
115451.22 |
1.6756899 |
0.2245905 |
| Resíduos |
10 |
688977.3 |
68897.73 |
|
|
Modelo para y3 : Tabela de Coeficientes
|
Estimativa |
Desvio Padrão |
Estat. t |
P-valor |
2.5% |
97.5% |
| Intercepto |
3386.1538 |
72.7999 |
46.5132 |
0 |
3223.9456 |
3548.3621 |
| x1 |
0.1205 |
0.1313 |
0.9181 |
0.3802 |
-0.172 |
0.413 |
| x2 |
0.1699 |
0.1313 |
1.2945 |
0.2246 |
-0.1226 |
0.4624 |
Modelo para y3 : Medida Descritiva da Qualidade do Ajuste
| Desvio Padrão dos Resíduos |
Graus de Liberdade |
$R^2$ |
$R^2$ Ajustado |
| 262.4838 |
10 |
0.201192 |
0.04143148 |
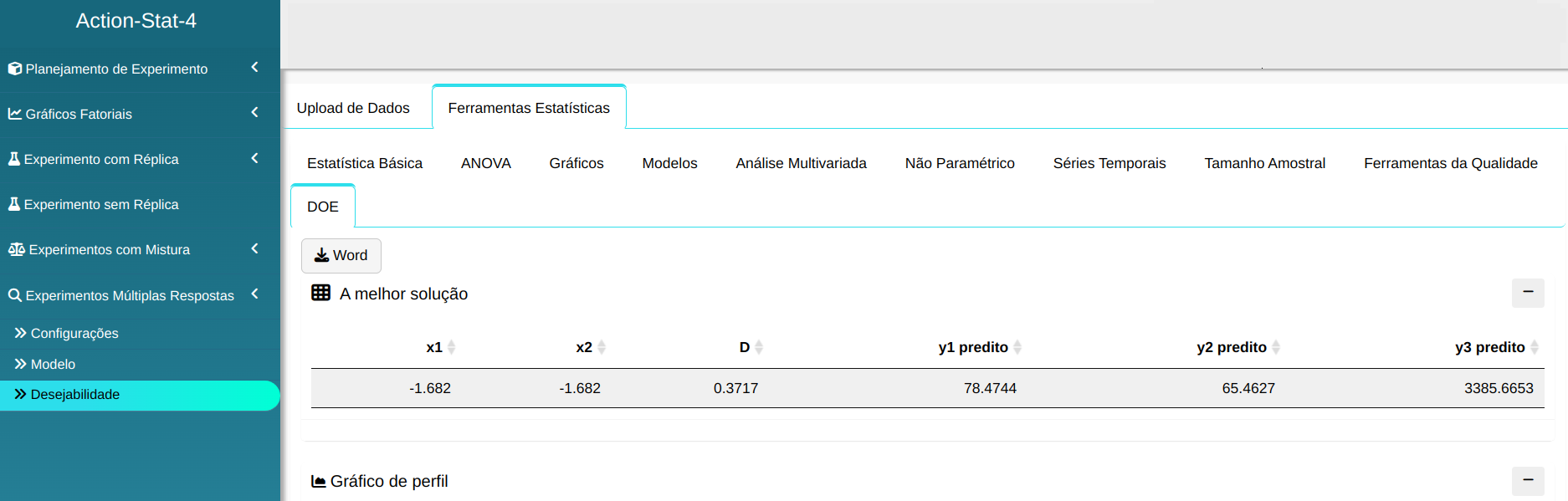
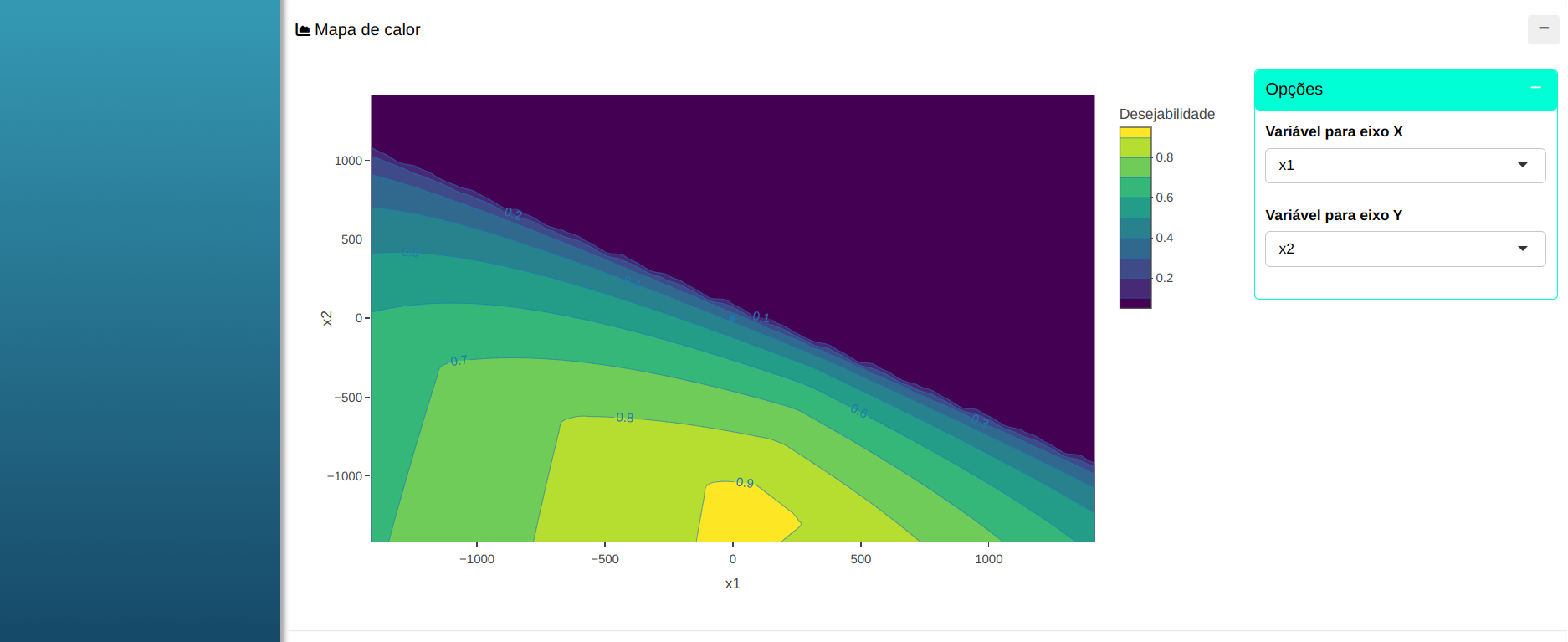
Em na janela da “Desejabilidade” Mostra-se qual é a melhor solução junto com o mapa de calor.
A melhor solução
| x1 |
x2 |
D |
y1 Predito |
y2 Predito |
y3 Predito |
| -1.682 |
-1.682 |
0.3717 |
78.4744 |
65.4627 |
3385.6653 |
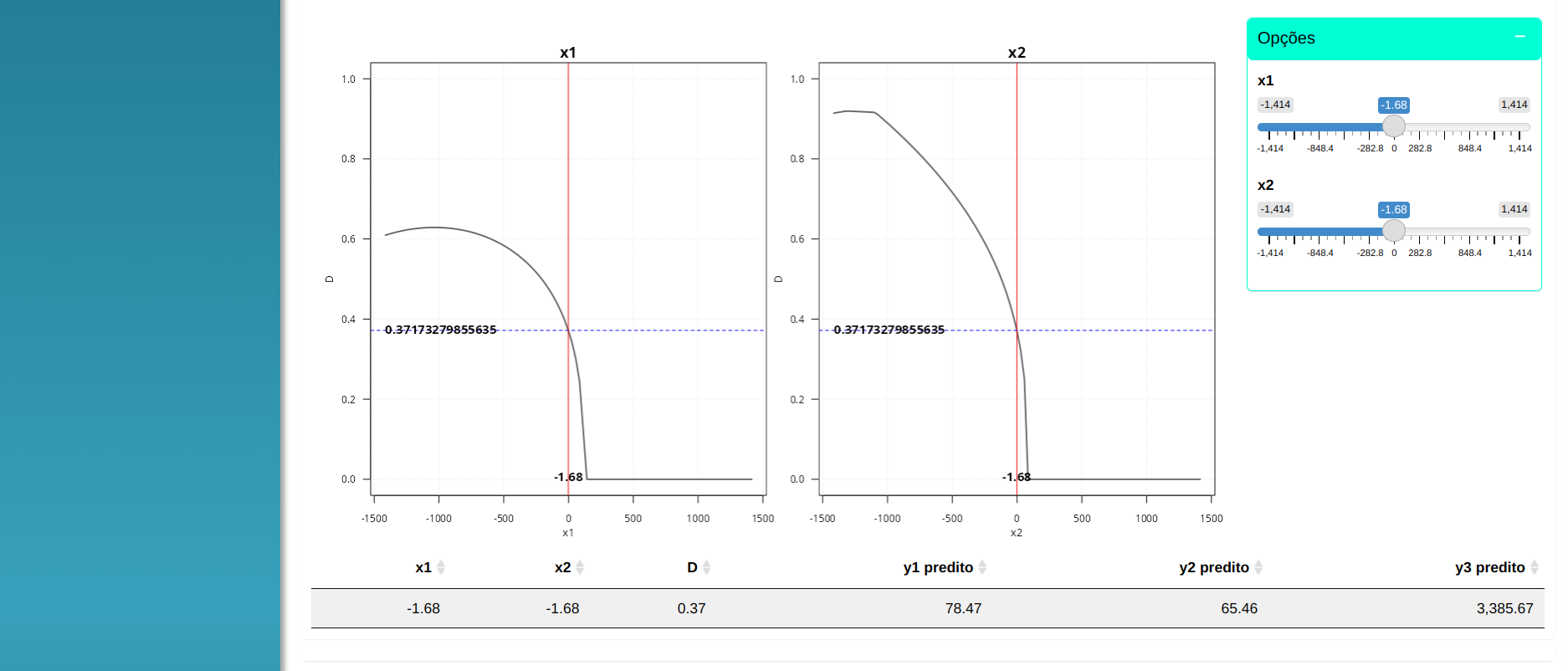
Gráfico de Perfil
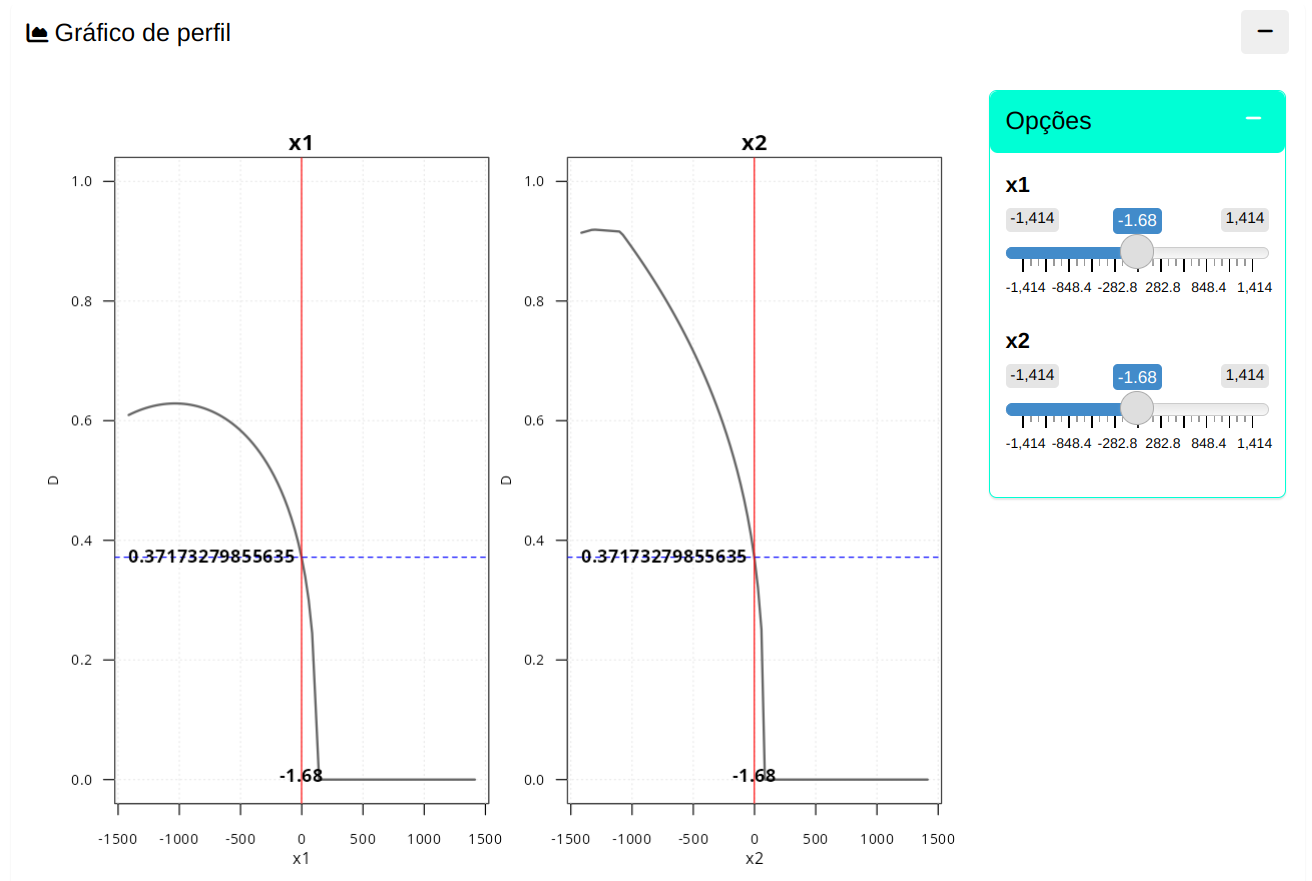
| x1 |
x2 |
D |
y1 Predito |
y2 Predito |
y3 Predito |
| -1.68 |
-1.68 |
0.37 |
78.47 |
65.46 |
3385.67 |
Mapa de Calor
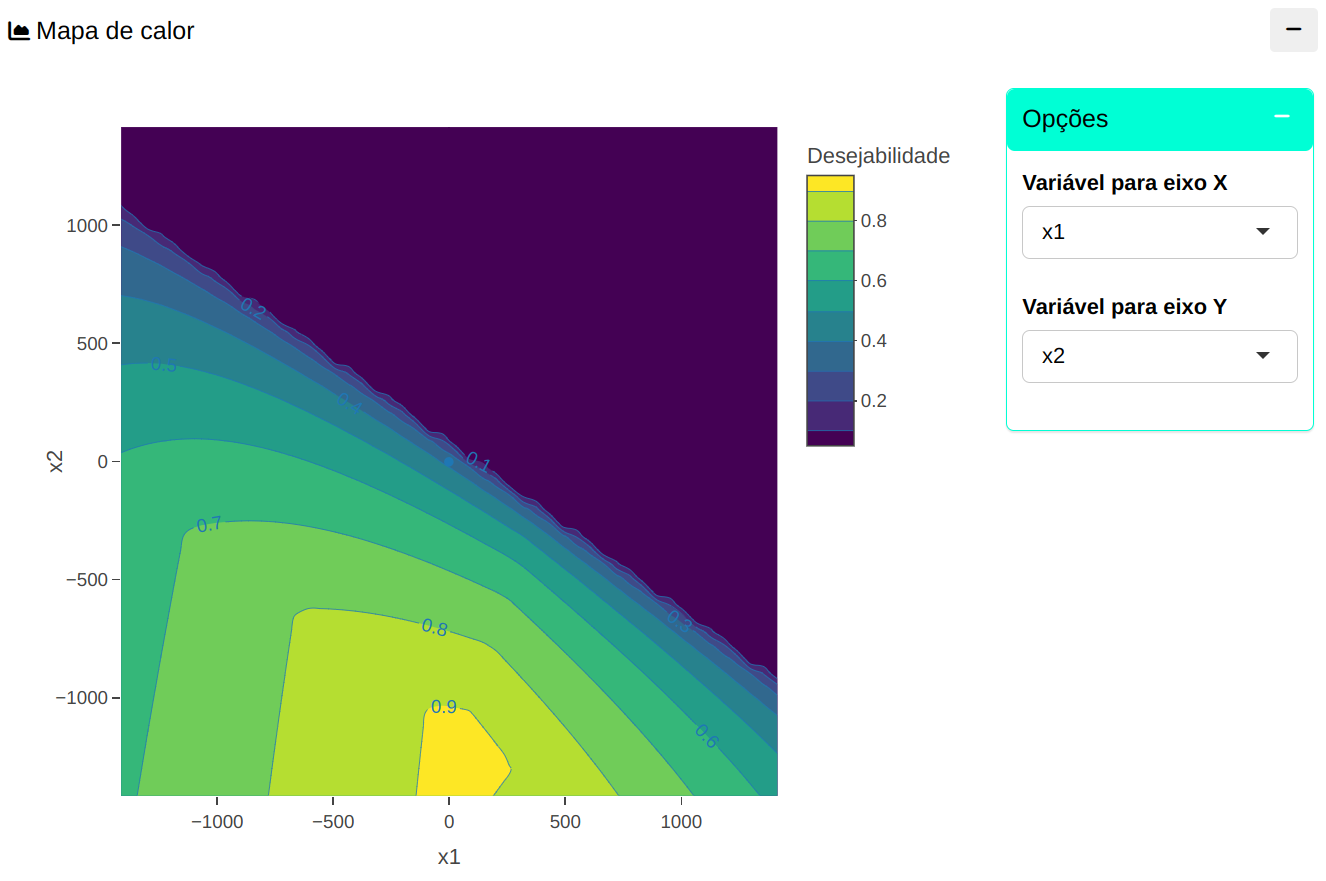
| x1 |
x2 |
D |
y1 Predito |
y2 Predito |
y3 Predito |
| 0 |
0 |
0.3676 |
78.4769 |
65.4615 |
3386.1538 |













