15. Distribuições
A ferramenta Distribuições do Action calcula a densidade, quantil e o percentil de diversas distribuições contínuas e discretas.
Exemplo 1:
Considere X uma variável aleatória Normal com média 11,15 e desvio padrão 2,238. Calcule a densidade de probabilidade.
| 7,57 |
| 12,29 |
| 10,35 |
| 16,28 |
| 11,79 |
| 10,17 |
| 10,77 |
| 11,27 |
| 7,39 |
| 8,25 |
| 8,39 |
| 12,27 |
| 12,82 |
| 12,26 |
| 12,07 |
| 9,72 |
| 8,45 |
| 8,67 |
| 11,17 |
| 8,40 |
| 11,92 |
| 9,39 |
| 9,62 |
| 18,53 |
| 11,67 |
| 8,75 |
| 9,63 |
| 13,06 |
| 4,69 |
| 12,43 |
| 7,69 |
| 10,64 |
| 10,55 |
| 8,85 |
| 6,02 |
| 8,88 |
| 15,46 |
| 12,79 |
| 11,27 |
| 8,01 |
| 9,69 |
| 9,91 |
| 8,43 |
| 12,88 |
| 11,50 |
| 9,82 |
| 14,55 |
| 9,88 |
| 13,25 |
| 10,35 |
Faremos o Upload dos dados no sistema.
Para calcular a densidade de probabilidade, a seguinte configuração é realizada, conforme mostrado na figura a seguir.
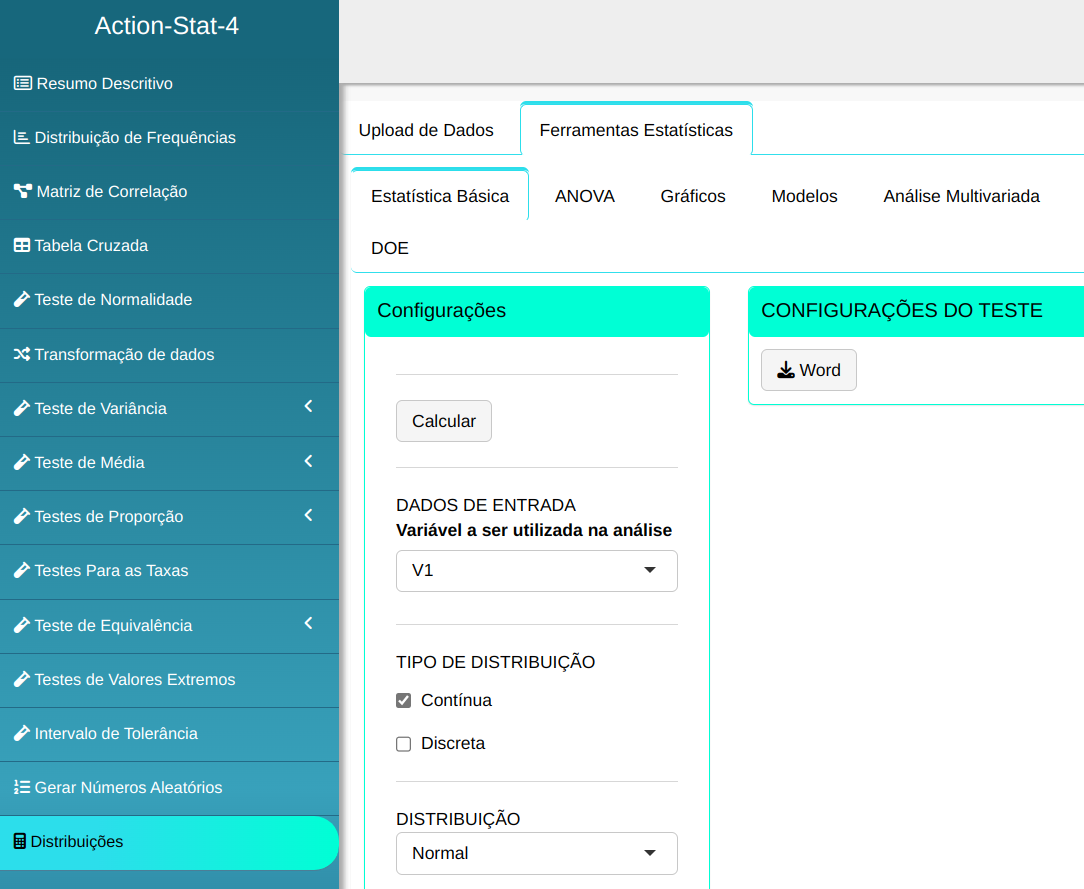
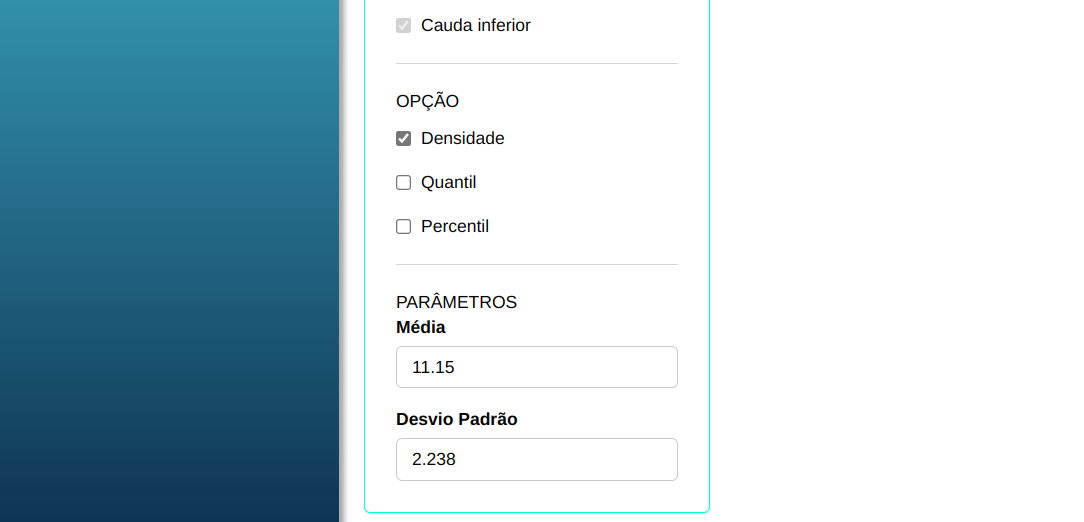
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
| Resultados |
|---|
| 0.050 |
| 0.157 |
| 0.167 |
| 0.013 |
| 0.171 |
| 0.162 |
| 0.176 |
| 0.178 |
| 0.044 |
| 0.077 |
| 0.083 |
| 0.157 |
| 0.135 |
| 0.157 |
| 0.164 |
| 0.145 |
| 0.086 |
| 0.097 |
| 0.178 |
| 0.084 |
| 0.168 |
| 0.131 |
| 0.141 |
| 0.001 |
| 0.174 |
| 0.100 |
| 0.141 |
| 0.124 |
| 0.003 |
| 0.151 |
| 0.054 |
| 0.174 |
| 0.172 |
| 0.105 |
| 0.013 |
| 0.106 |
| 0.028 |
| 0.136 |
| 0.178 |
| 0.066 |
| 0.144 |
| 0.153 |
| 0.085 |
| 0.132 |
| 0.176 |
| 0.150 |
| 0.056 |
| 0.152 |
| 0.115 |
| 0.167 |
Exemplo 2:
Considere X uma variável aleatória Normal com média 11,15 e desvio padrão 2,238. Vamos calcular determinados percentis desta distribuição.
| V1 |
|---|
| 7,57 |
| 12,29 |
| 10,35 |
| 16,28 |
| 11,79 |
| 10,17 |
| 10,77 |
| 11,27 |
| 7,39 |
| 8,25 |
| 8,39 |
| 12,27 |
| 12,82 |
| 12,26 |
| 12,07 |
| 9,72 |
| 8,45 |
| 8,67 |
| 11,17 |
| 8,4 |
| 11,92 |
| 9,39 |
| 9,62 |
| 18,53 |
| 11,67 |
| 8,75 |
| 9,63 |
| 13,06 |
| 4,69 |
| 12,43 |
| 7,69 |
| 10,64 |
| 10,55 |
| 8,85 |
| 6,02 |
| 8,88 |
| 15,46 |
| 12,79 |
| 11,27 |
| 8,01 |
| 9,69 |
| 9,91 |
| 8,43 |
| 12,88 |
| 11,5 |
| 9,82 |
| 14,55 |
| 9,88 |
| 13,25 |
| 10,35 |
Faremos o upload dos dados no sistema.
Para calcular os percentis, a seguinte configuração é realizada, conforme mostrado na figura a seguir.
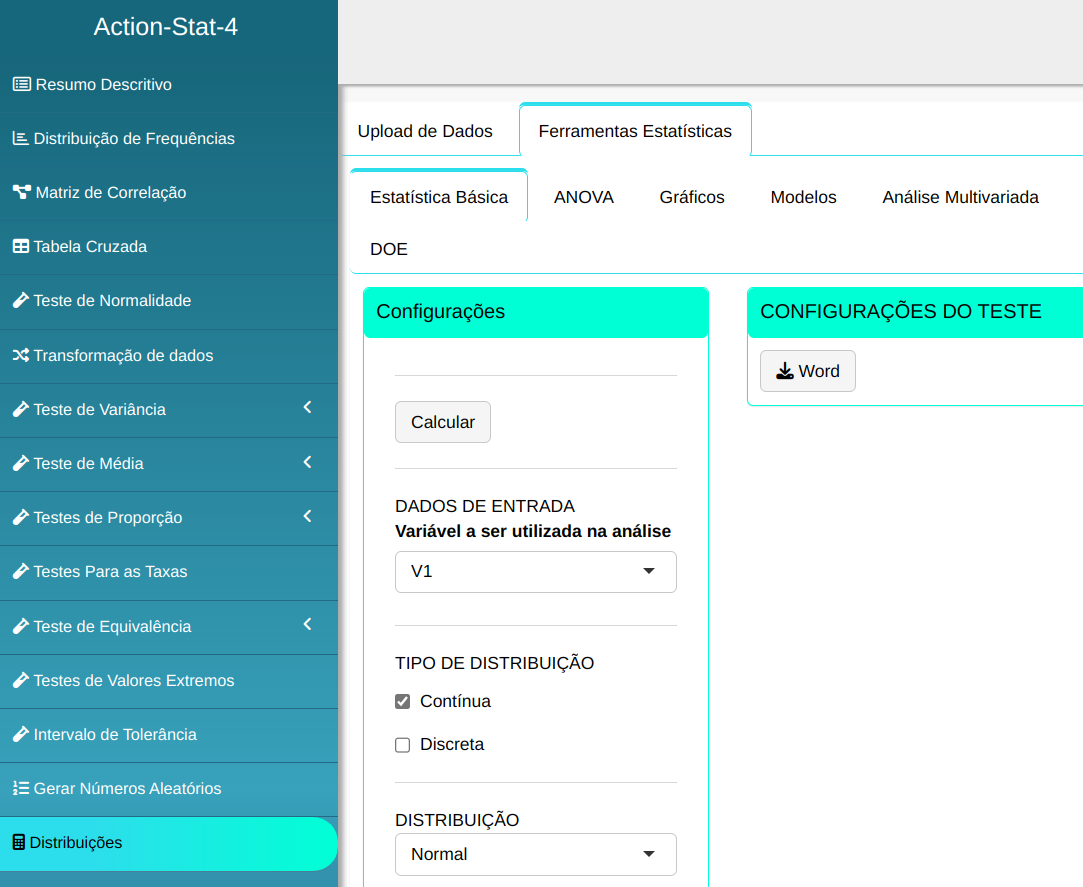
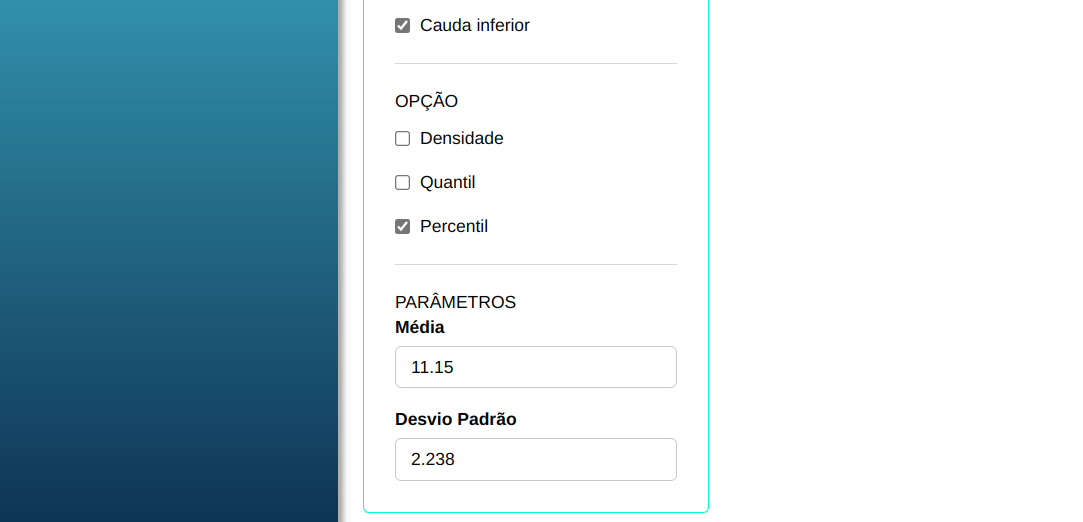
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
| Resultados |
|---|
| 0.055 |
| 0.695 |
| 0.360 |
| 0.989 |
| 0.612 |
| 0.331 |
| 0.432 |
| 0.522 |
| 0.047 |
| 0.097 |
| 0.109 |
| 0.692 |
| 0.772 |
| 0.691 |
| 0.659 |
| 0.262 |
| 0.114 |
| 0.134 |
| 0.504 |
| 0.109 |
| 0.634 |
| 0.215 |
| 0.247 |
| 1.000 |
| 0.591 |
| 0.142 |
| 0.248 |
| 0.804 |
| 0.002 |
| 0.716 |
| 0.061 |
| 0.411 |
| 0.394 |
| 0.152 |
| 0.011 |
| 0.155 |
| 0.973 |
| 0.768 |
| 0.521 |
| 0.080 |
| 0.257 |
| 0.289 |
| 0.112 |
| 0.780 |
| 0.562 |
| 0.277 |
| 0.936 |
| 0.285 |
| 0.826 |
| 0.360 |
Exemplo 3:
Considere X uma variável aleatória Normal com média 11,15 e desvio padrão 2,238. Vamos calcular determinados quantis desta distribuição.
Primeiramente vamos digitar as probabilidades das quais queremos descobrir os quantis da distribuição de interesse.
Enviaremos os dados para o sistema.
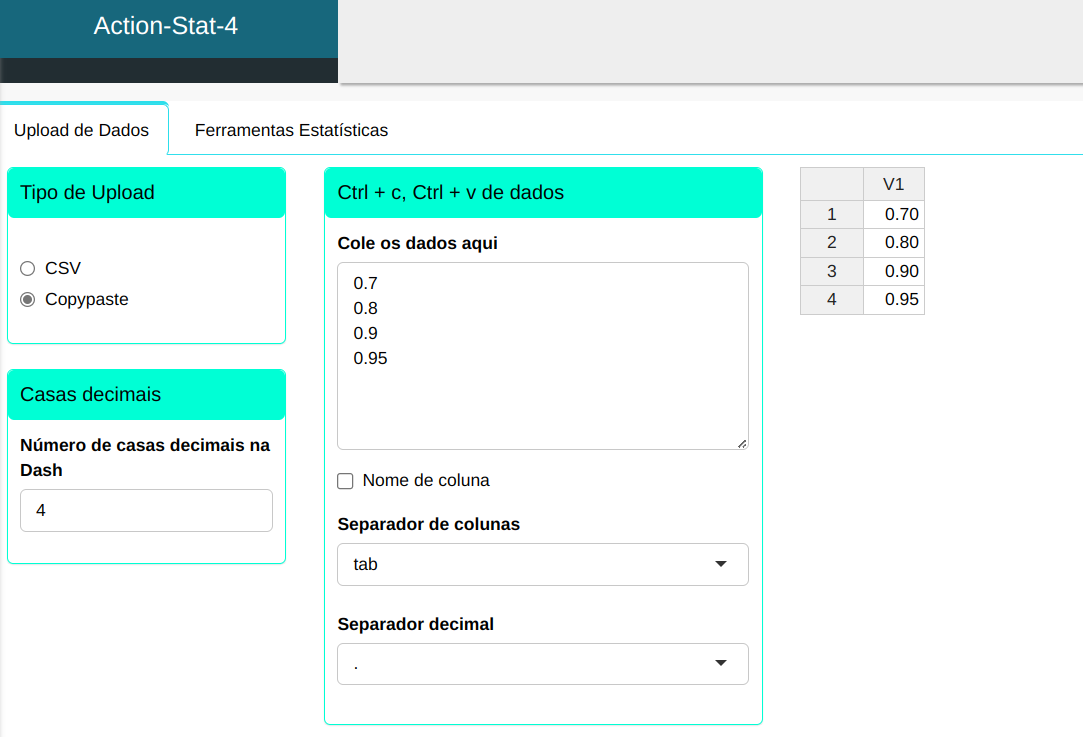
Para calcular os quantis, a seguinte configuração é realizada, conforme mostrado na figura a seguir.
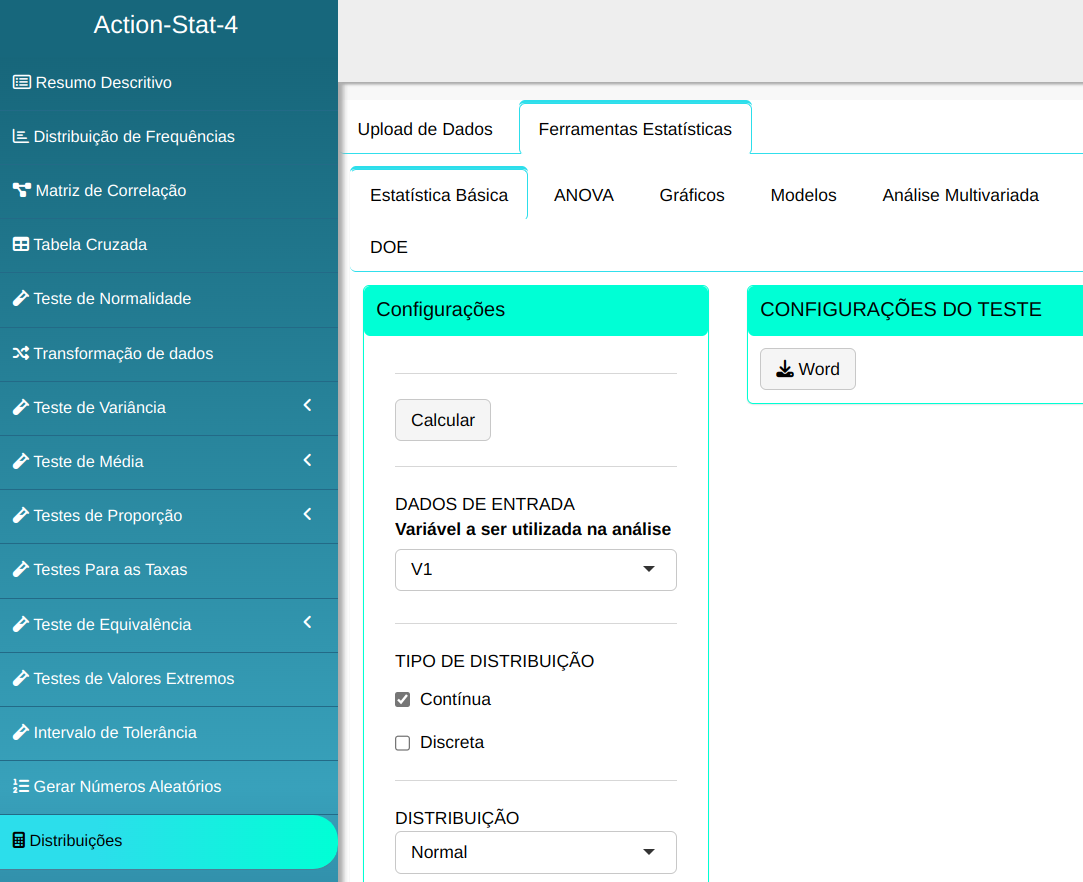
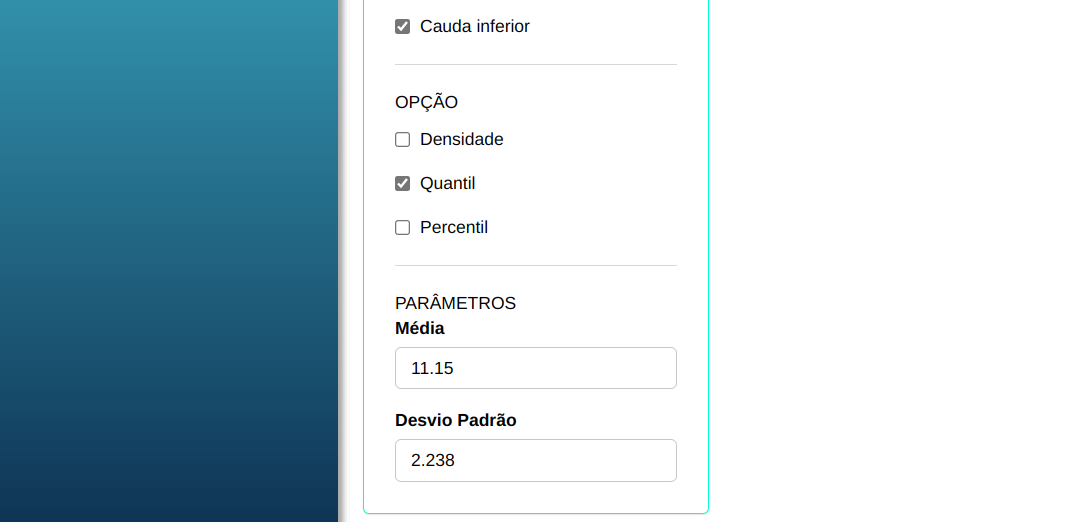
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.S

Os resultados são:
| Resultados |
|---|
| 12.32361 |
| 13.03355 |
| 14.01811 |
| 14.83118 |
Exemplo 4:
Suponha que numa linha de produção a probabilidade de se obter uma peça defeituosa (sucesso) é p=0,1. Toma-se uma amostra de 4 peças para serem inspecionadas. Qual a probabilidade de se obter uma peça defeituosa, nenhuma peça defeituosa, 2 peças defeituosas, 3 e 4 peças defeituosas?
Primeiramente vamos digitar os possiveis valores que a variável aleatória pode assumir, nesse caso seria a quantidade de peças que podem ser defeituosas
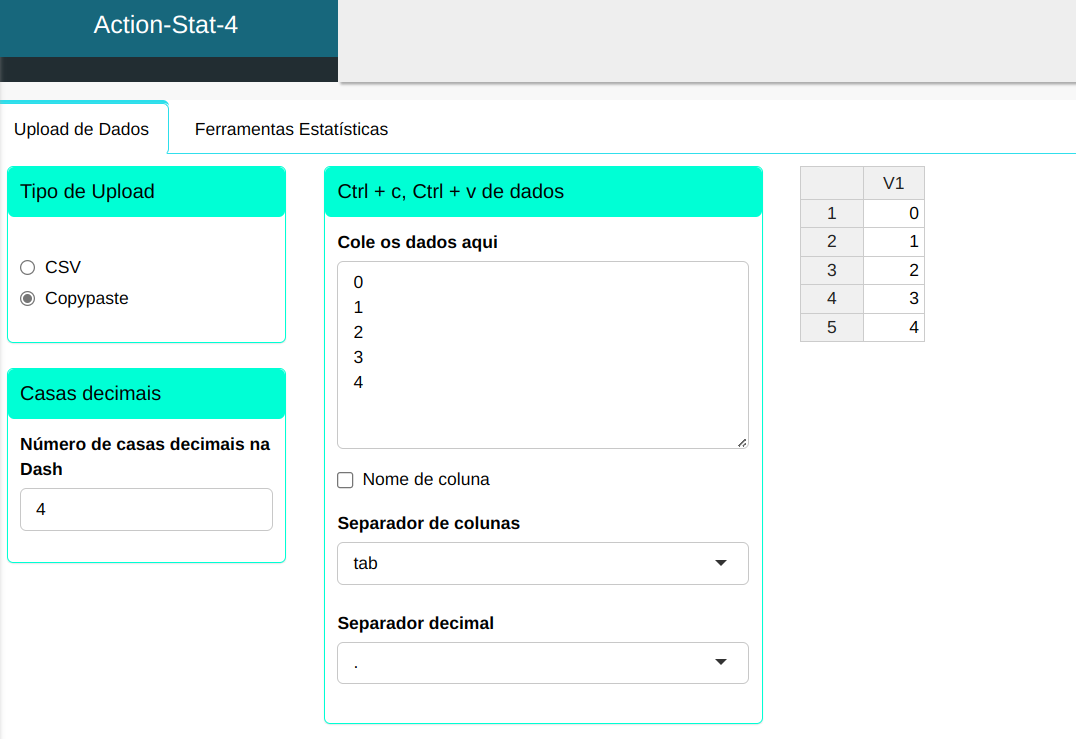
Para calcular a densidade de probabilidade, a seguinte configuração é realizada, conforme mostrado na figura a seguir.
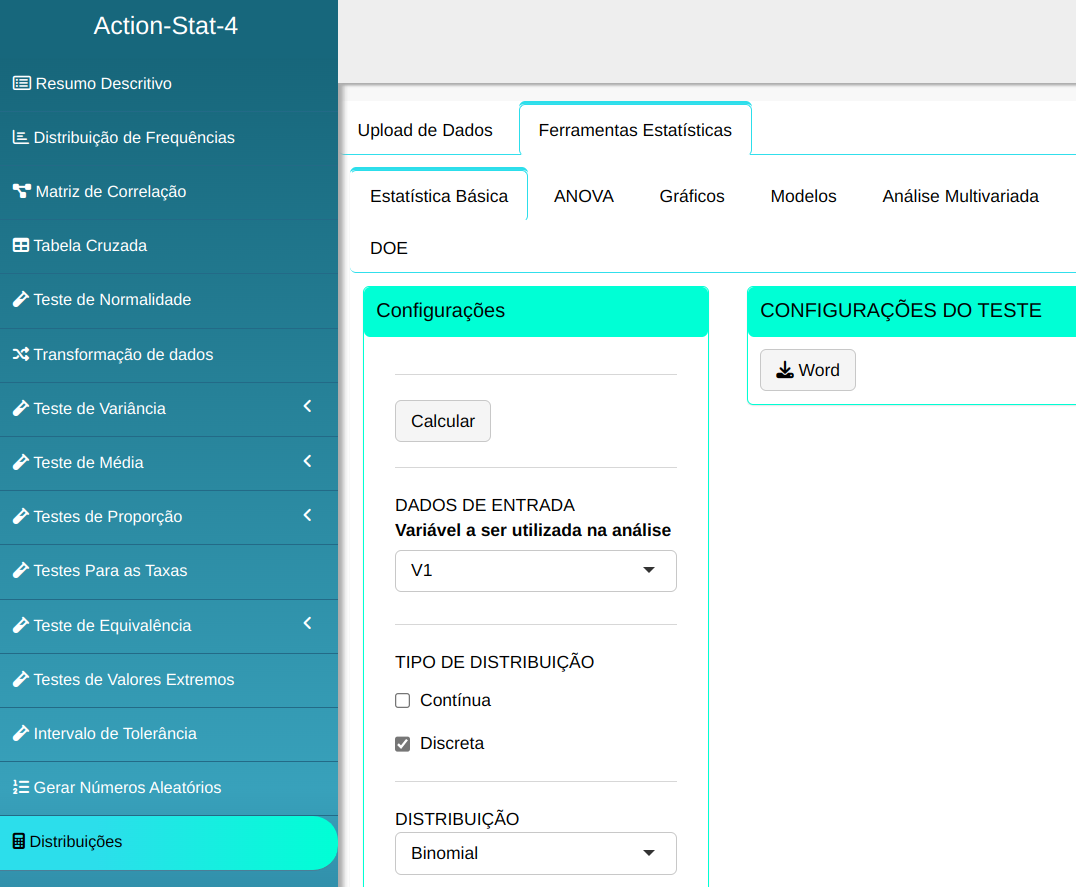
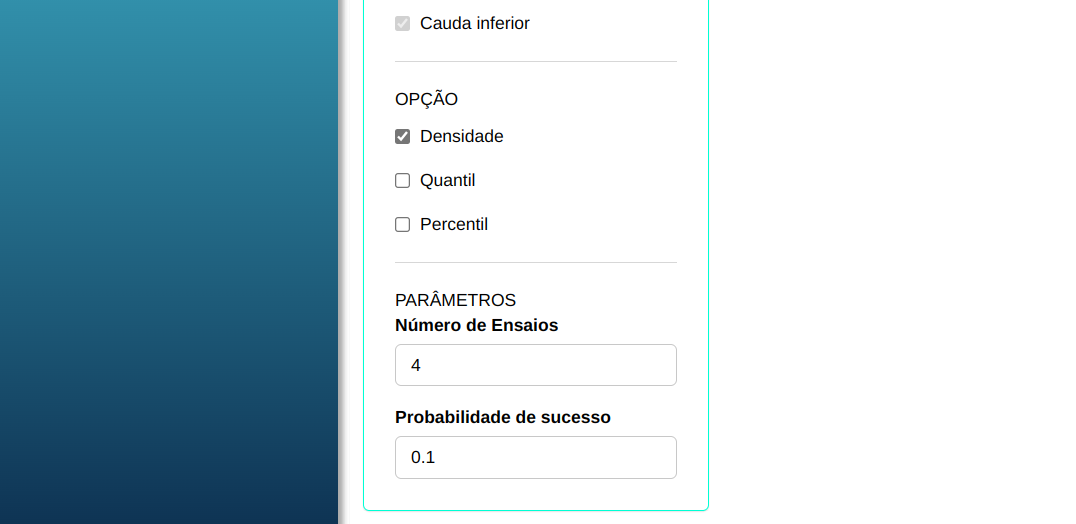
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
| Resultados |
|---|
| 0.6561 |
| 0.2916 |
| 0.0486 |
| 0.0036 |
| 0.0001 |
Pela tabela, vemos que as probabilidades de se obter uma peça defeituosa é de 29,16%, nenhuma peça defeituosa é de 65,61%, e de se obter duas peças defeituosas é 4,86% e para mais que duas é menos que 1%.
Exemplo 5:
Considere uma variável aleatória X com distribuição Binomial com parâmetro n=10 e prob=0,1. Calcule o quantil de X ser menor que 0,8 (80%), 0,9 (90%), 0,95 (95%) e 0,975 (97,5%).
Primeiramente vamos digitar as probabilidades das quais queremos descobrir os quantis da distribuição de interesse
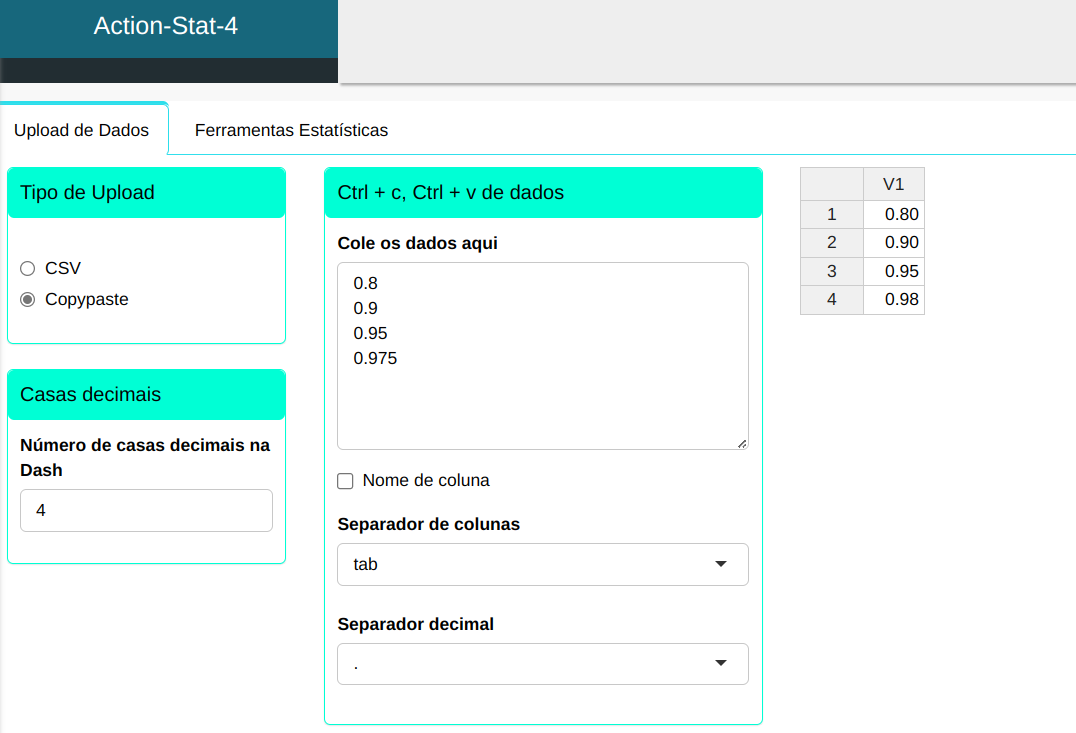
Para calcular os quantis, a seguinte configuração é realizada, conforme mostrado na figura a seguir.
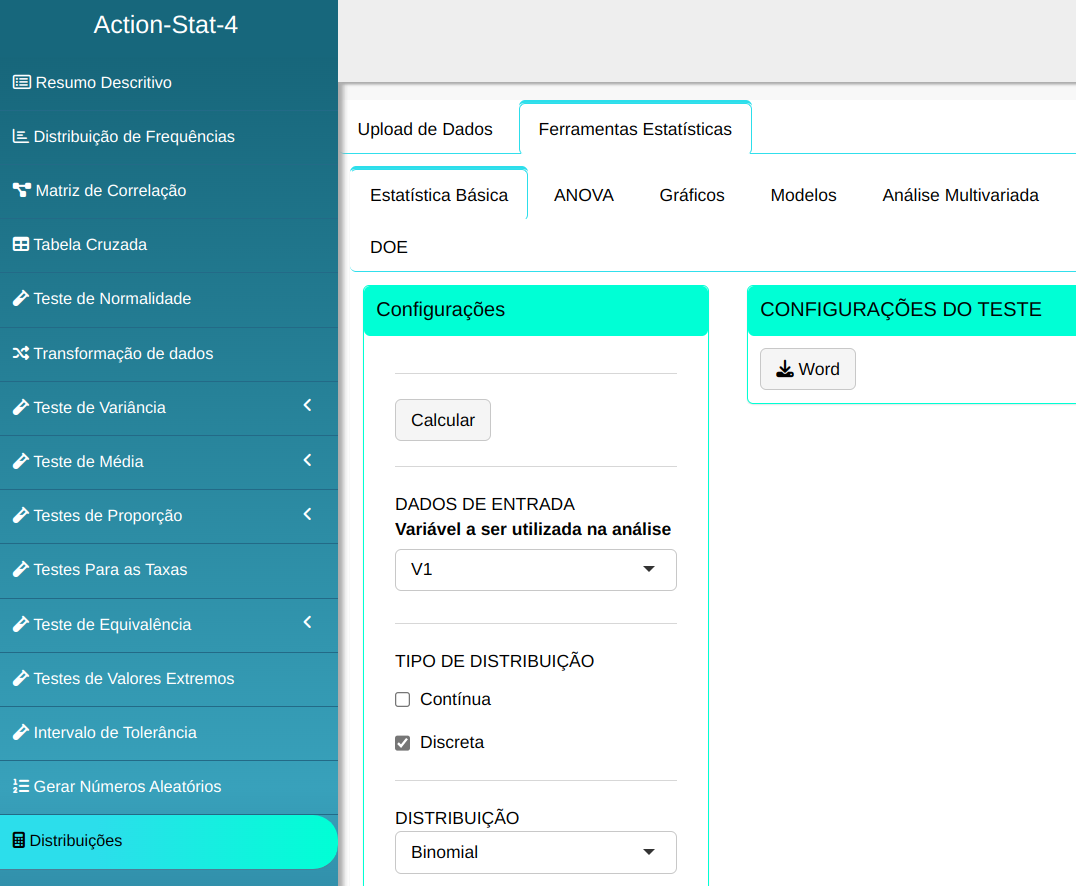
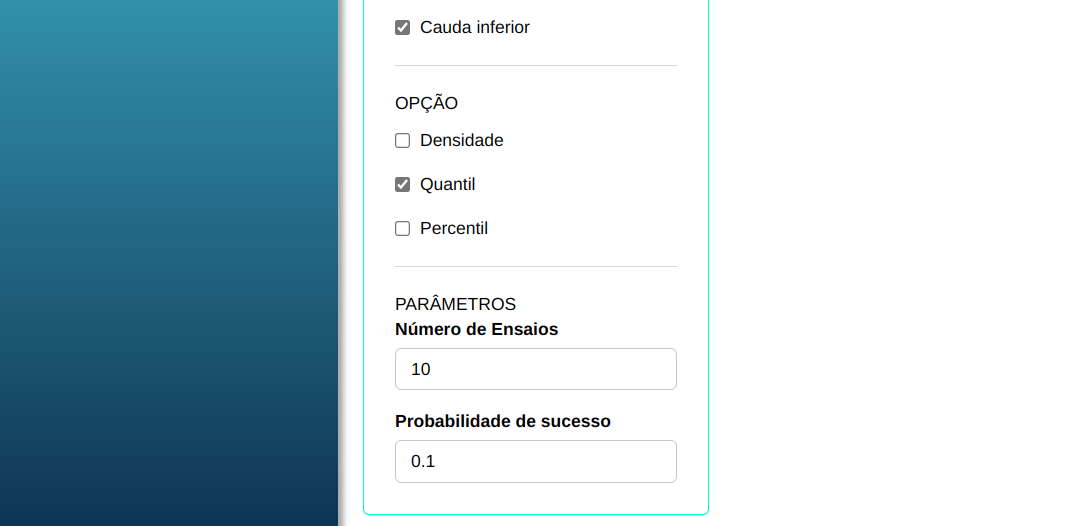
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
| Resultados |
|---|
| 2 |
| 2 |
| 3 |
| 3 |
Se o processo é um experimento de 10 tentativas com probabilidade de sucesso de 10%,
- Em 80% dos casos, observamos no máximo 2 sucessos.
- Em 90% dos casos, observamos no máximo 2 sucessos.
- Em 95% dos casos, observamos no máximo 3 sucessos.
- Em 97,5% dos casos, observamos no máximo 3 sucessos.
Exemplo 6:
Suponha que numa linha de produção a probabilidade de se obter uma peça defeituosa (sucesso) é p=0,1. Toma-se uma amostra de 10 peças para serem inspecionadas. Qual a probabilidade de se obter 3 defeitos ou menos?
Primeiramente vamos digitar o valor onde calcularemos o percentil
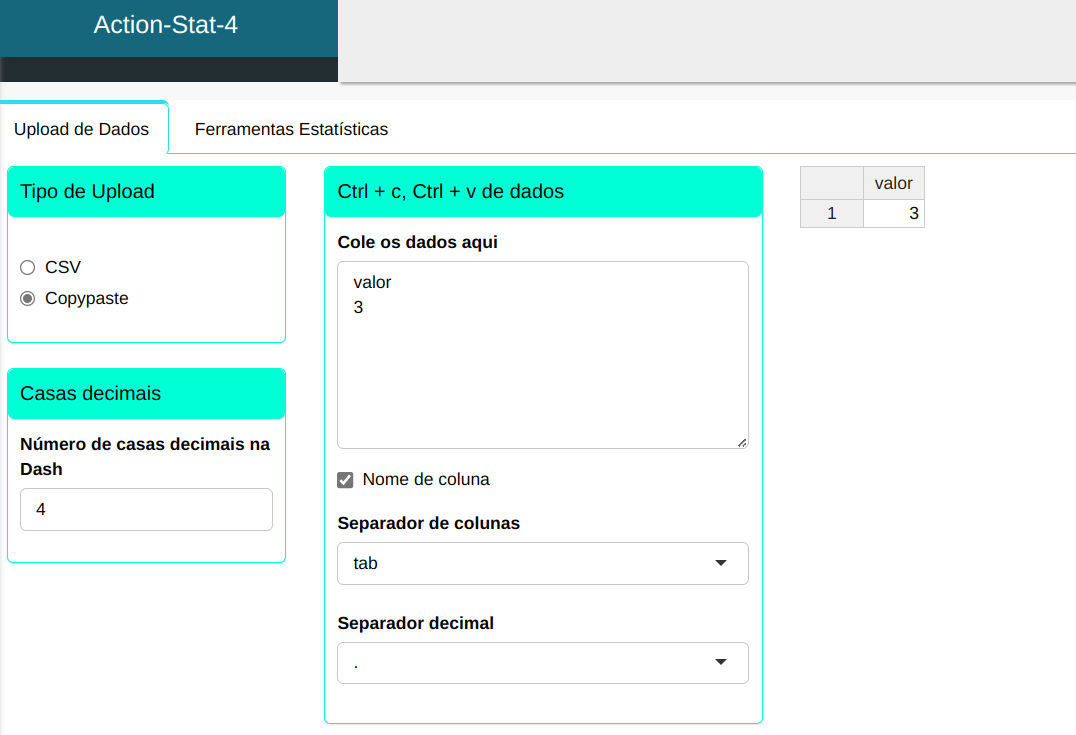
Para calcular os percentis, a seguinte configuração é realizada, conforme mostrado na figura a seguir.
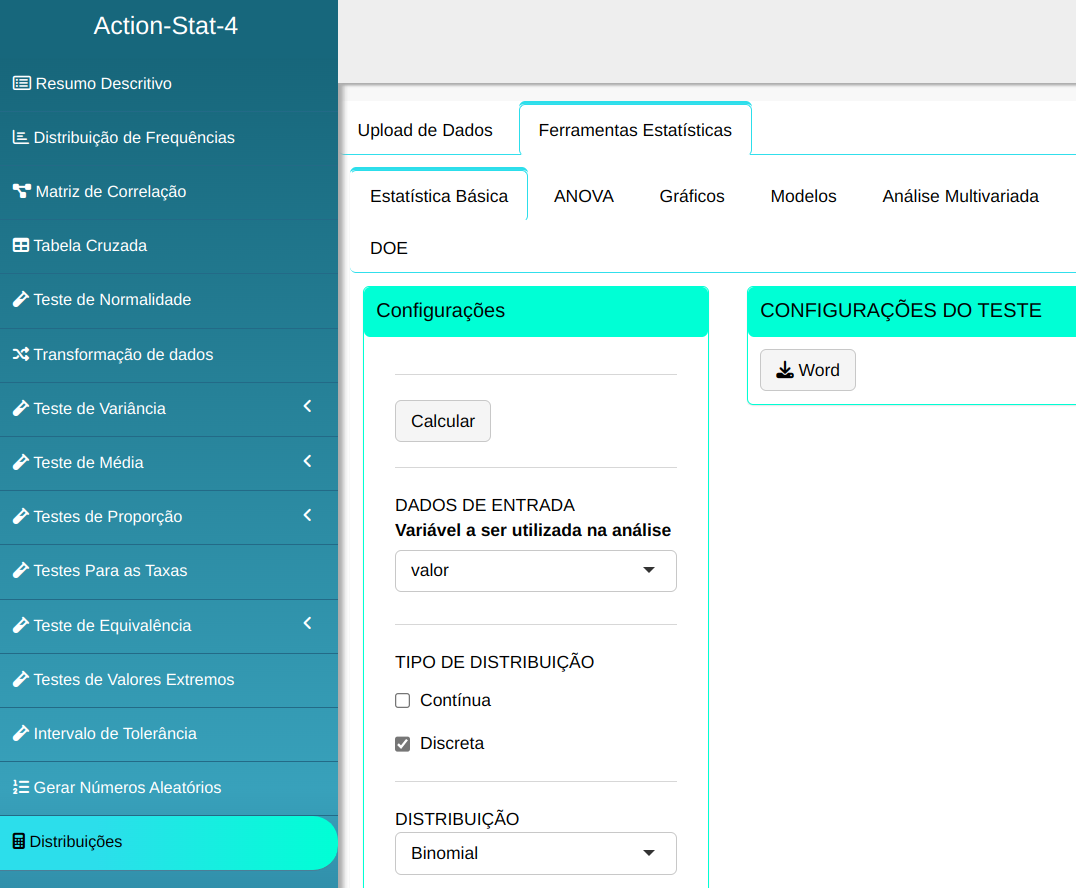
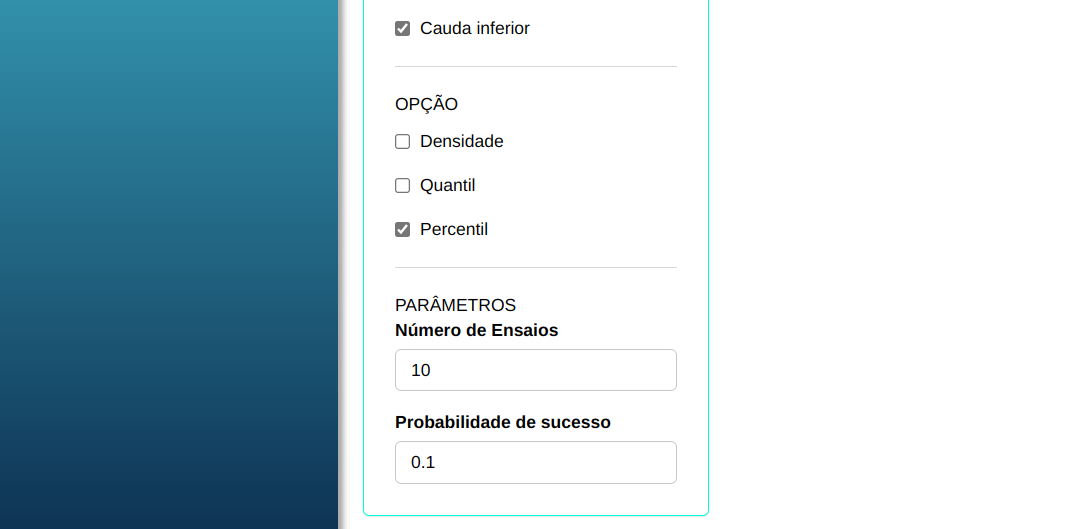
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Obtemos os resultados.
| vetNum |
|---|
| 0.9872048 |
Pelo valor liberado, temos que a probabilidade de obter 3 defeitos ou menos é de aproximadamente 98,72%.