13. Intervalo de Tolerância

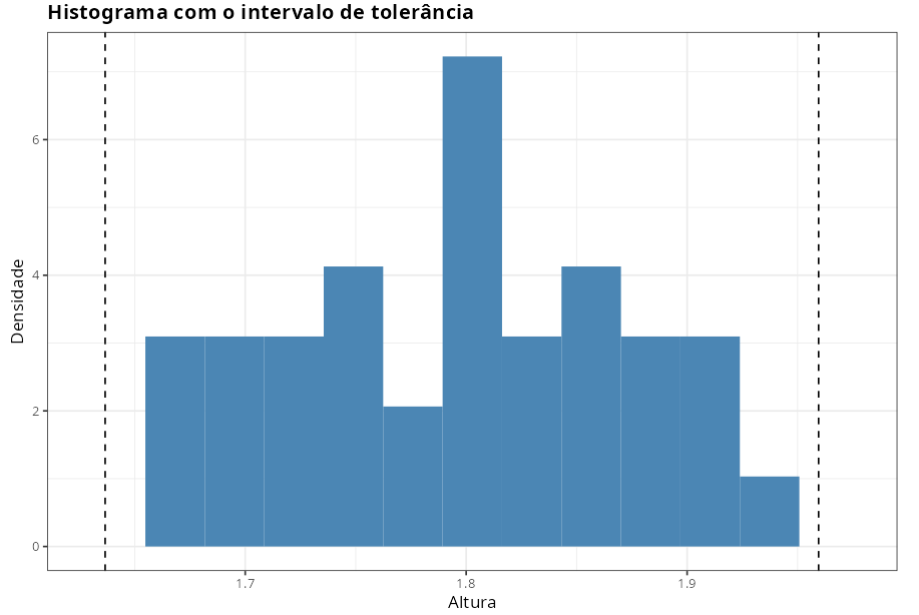
O Intervalo de Tolerância define os limites superiores e/ou inferiores dentro dos quais uma determinada porcentagem caracteristica/especifica cai em um nível de confiança declarado.

Exemplo:

Pretende-se determinar uma porcentagem de 90% da população com um nível de confiança de 95%.

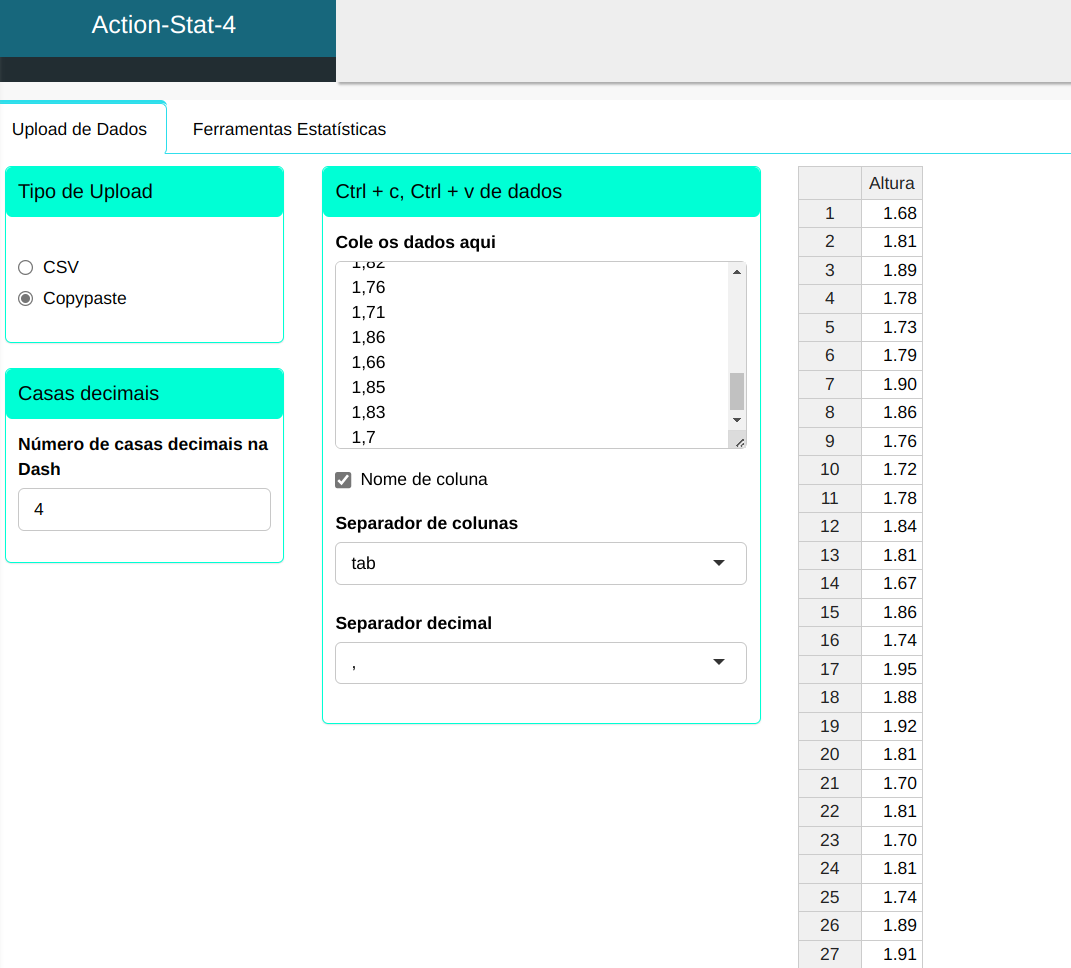
Altura
1,68
1,81
1,89
1,78
1,73
1,79
1,90
1,86
1,76
1,72
1,78
1,84
1,81
1,67
1,86
1,74
1,95
1,88
1,92
1,81
1,70
1,81
1,70
1,81
1,74
1,89
1,91
1,80
1,82
1,76
1,71
1,86
1,66
1,85
1,83
1,7

---

Faremos o upload dos dados no sistema

Para calcular o Intervalo de Tolerância, a seguinte configuração é realizada, conforme mostrado na figura a seguir.

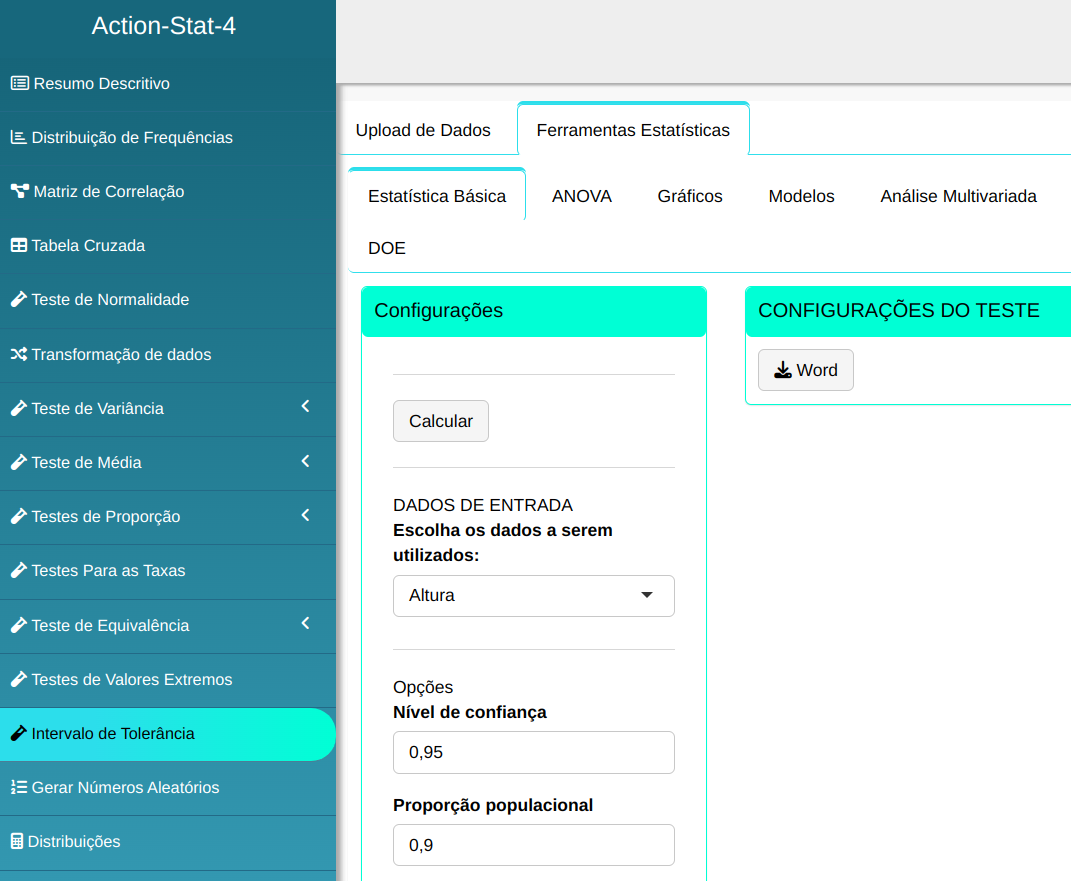
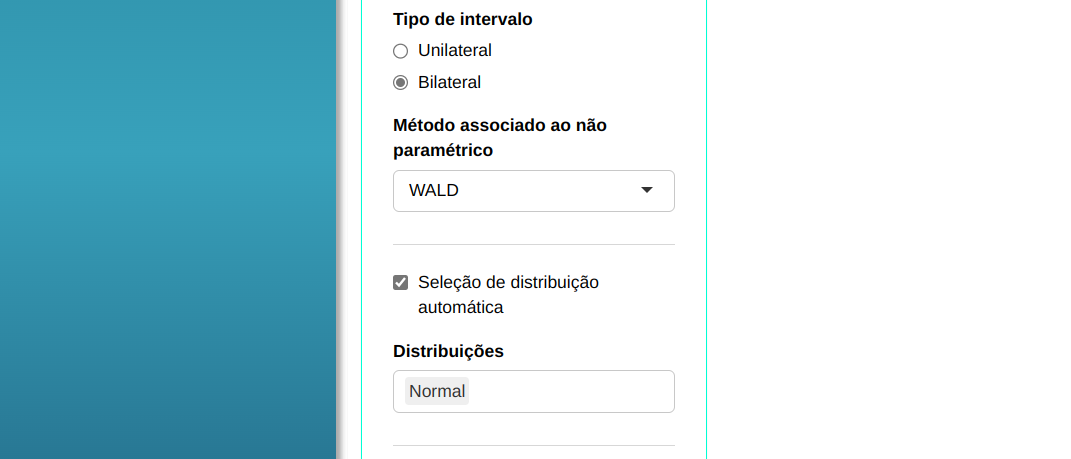
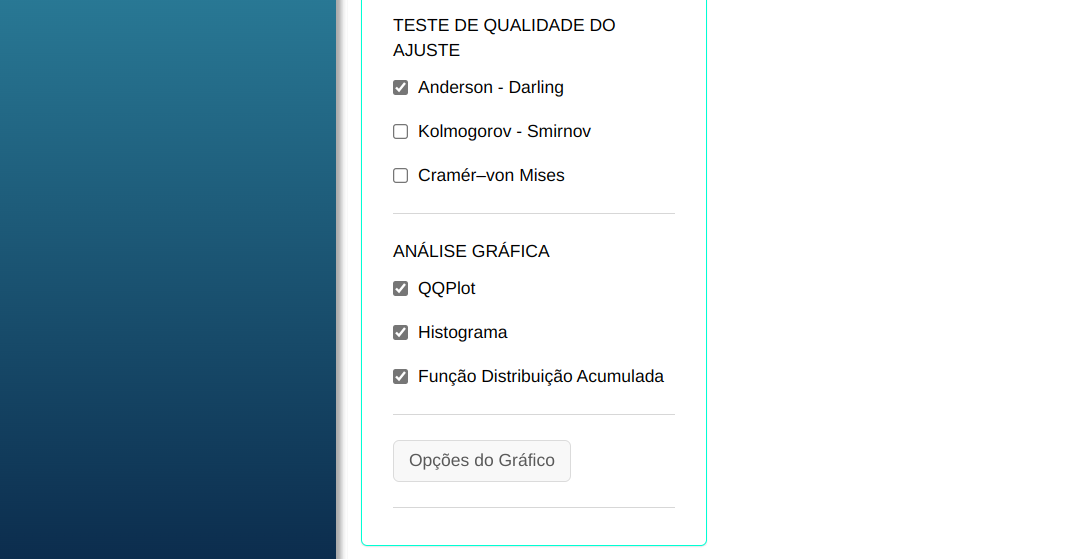
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

---

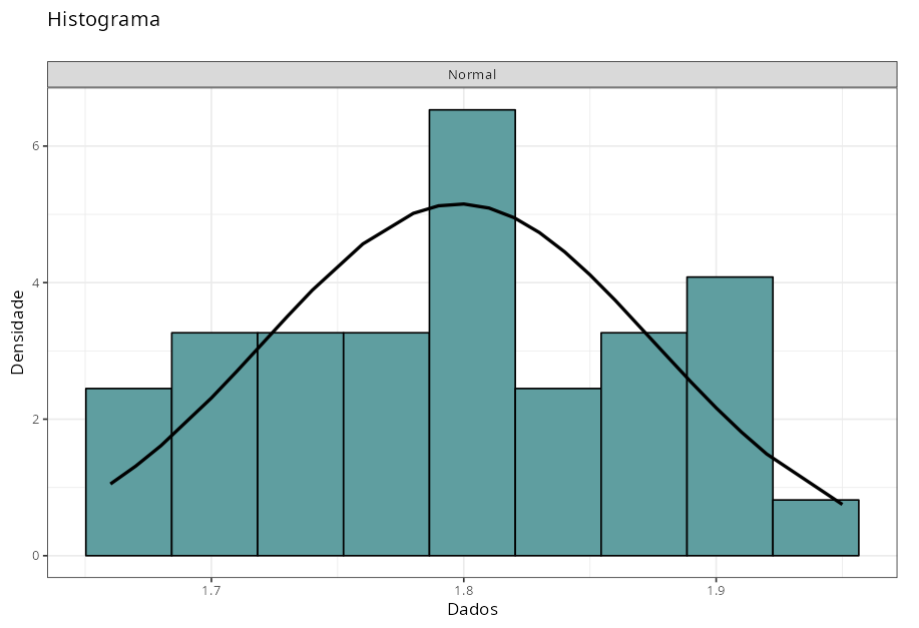
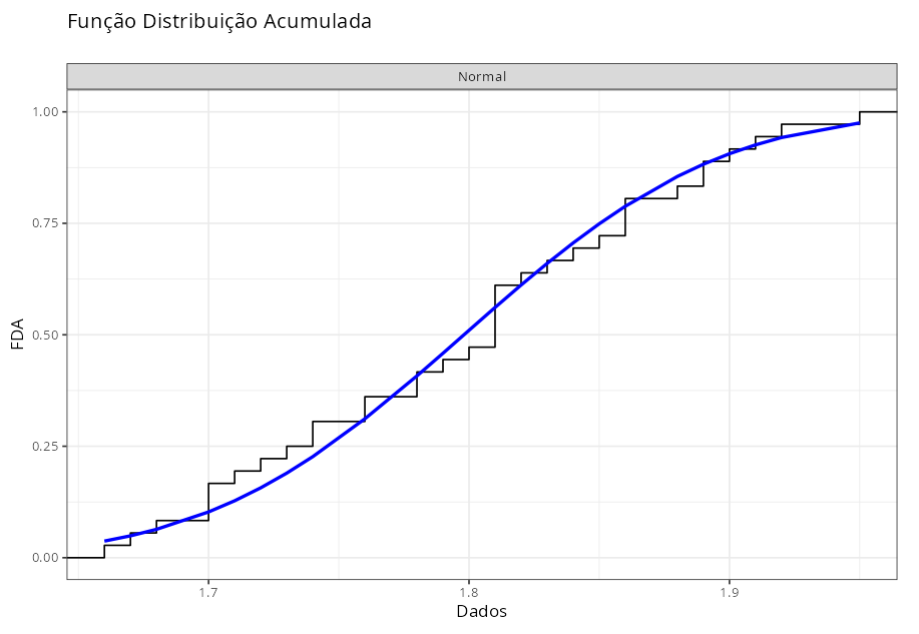
Os resultados são:

	Distribuição Ajustada
	$\quad \qquad$Normal

---

Intervalo de Tolerância

Nível de Significância	Proporção Populacional	Limite Inferior	Limite Superior
0.05	0.900	1.637	1.959

---

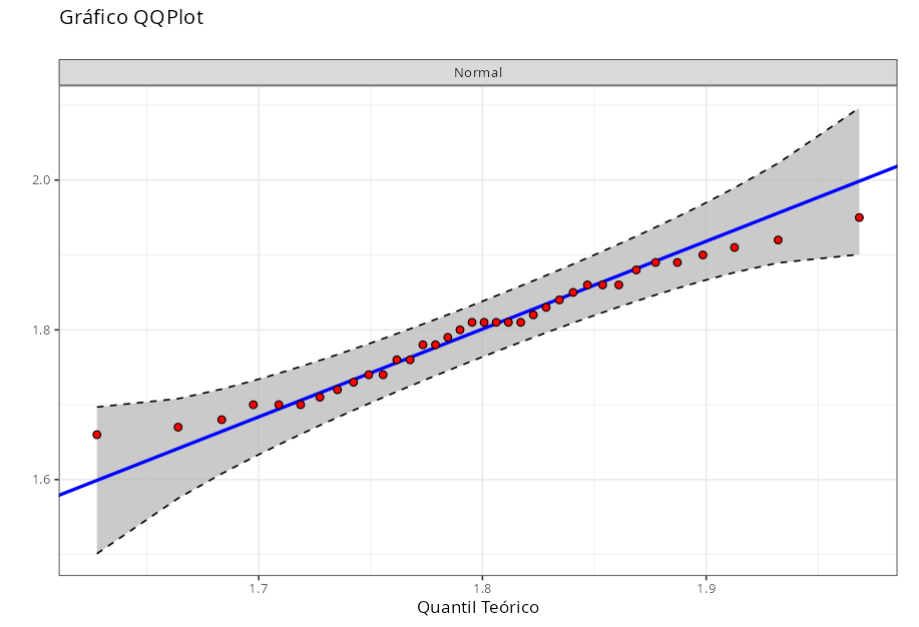
Anderson-Darling

Distribuições	Estatística	P-Valor
Normal ($ \mu = 1.8, \quad \sigma = 0.077$)	0.291	0.589

---