1. Resumo Descritivo
Etapa inicial de uma análise, usada para descrever, organizar e resumir os aspectos importantes dos dados coletados.
Detalhes
O resumo descritivo nos permite obter diversas informações sobre o conjunto de dados: mínimo, máximo, soma, soma quadrática, tamanho da amostra, 1ºquartil, 3ºquartil e tri-média. Além destas informações, é possível realizar o cálculo de medidas de posição (média e mediana), medidas de dispersão (desvio padrão da média, desvio padrão, variância e amplitude) e outras estatísticas descritivas como assimetria e curtose.
Exemplo 1:
A medida do comprimento de 15 rolos de aço foi feita e faremos o upload no sistema:
| 71,16 |
| 71,62 |
| 62,86 |
| 65,30 |
| 65,58 |
| 67,95 |
| 65,72 |
| 63,25 |
| 70,93 |
| 68,78 |
| 78,76 |
| 72,42 |
| 74,09 |
| 66,79 |
| 72,78 |
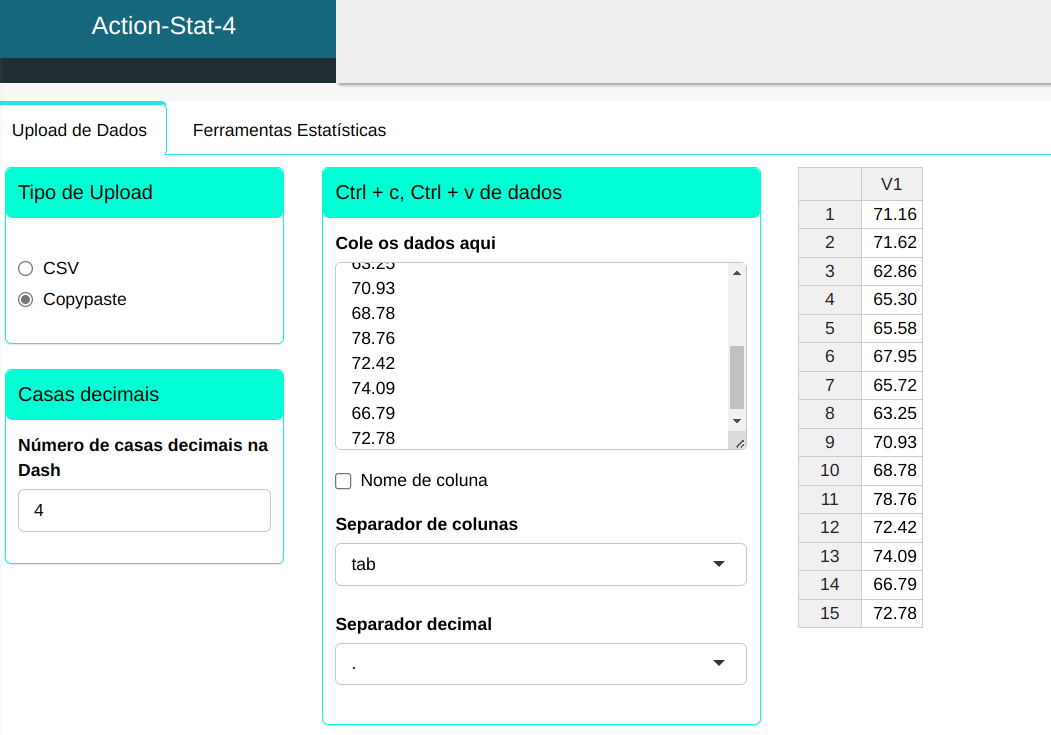
Configurando conforme a figura de abaixo para realizar o ressumo descritivo
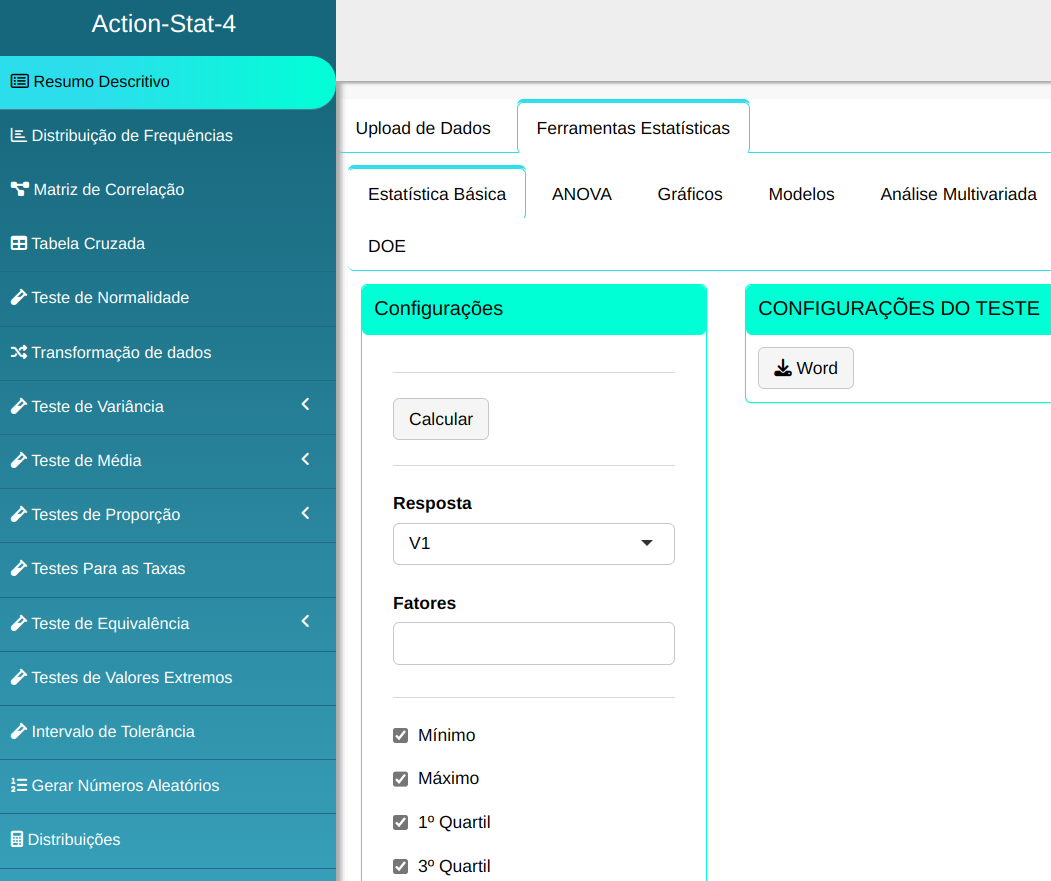
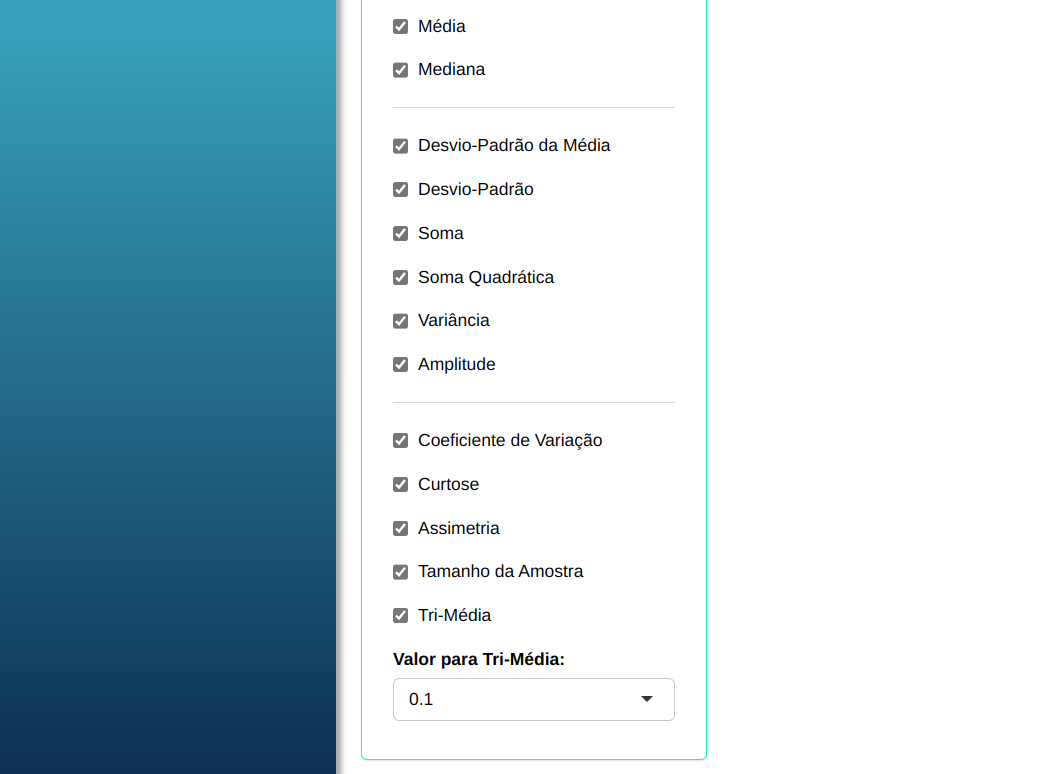
Clique em Calcular para visualizar os resultados e baixá-los em formato Word.

Obtemos os seguintes resultados:
| Estatística | Descritiva |
|---|---|
| Mínimo: | 62.86 |
| 1º Quartil: | 65.58 |
| Média: | 69.199333 |
| Mediana: | 68.78 |
| Tri-Média: | 68.951538 |
| 3º Quartil: | 72.42 |
| Máximo: | 78.76 |
| Soma: | 1.037.99 |
| Soma Quadrática: | 72102.9673 |
| Desvio Padrão da Média: | 1.1438267 |
| Desvio Padrão: | 4.430022 |
| Variância: | 19.625092 |
| Coeficiente de Variação: | 6.401827 |
| Assimetria: | 0.358057 |
| Curtose: | -0.799861 |
| Amplitude: | 15.900 |
| Tamanho da Amostra: | 15 |
A média e a mediana são representantes da distribuição global do comprimento dos rolos de fio na amostra.
-
A variabilidade resultante é considerável caso os comprimentos dos rolos de fio devam ser próximos. Isso pode ser visto através das medidas de dispersão.
-
A função de distribuição é mais achatada que a distribuição Normal, pois a Curtose é menor que zero. Já, como o valor da Assimetria é positivo, mas um valor pequeno, a função de distribuição tem cauda levemente mais longa do lado direito, ou seja, a distribuição é assimétrica à direita.
-
Tanto a média quanto a mediana podem ser consideradas representantes da distribuição geral dos dados da amostra, pois ambas tem valores próximos. No entanto, quando o valor da mediana é muito diferente da média, é aconselhável considerar sempre a mediana como valor de referência mais importante.
Exemplo 2:
A medição do diâmetro de peças foi efetuada por quatro operadores, A, B, C e D, nas mesmas condições. 6 peças foram escolhidas ao acaso e as medidas obtidas estão na Tabela a seguir. Neste caso temos um conjunto de dados com único fator, Operadores, e com quatro níveis, Operador A, Operador B, operador C e Operador D.
| Níveis | Dados |
|---|---|
| A | 1,688109 |
| A | 1,685566 |
| A | 1,672408 |
| A | 1,680943 |
| A | 1,679250 |
| A | 1,682141 |
| B | 1,663774 |
| B | 1,665943 |
| B | 1,669364 |
| B | 1,671857 |
| B | 1,665928 |
| B | 1,670507 |
| C | 1,658883 |
| C | 1,660408 |
| C | 1,663021 |
| C | 1,662004 |
| C | 1,661382 |
| C | 1,655508 |
| D | 1,672502 |
| D | 1,670928 |
| D | 1,683285 |
| D | 1,686528 |
| D | 1,677429 |
| D | 1,681030 |
Realizaremos então o resumo descritivo.
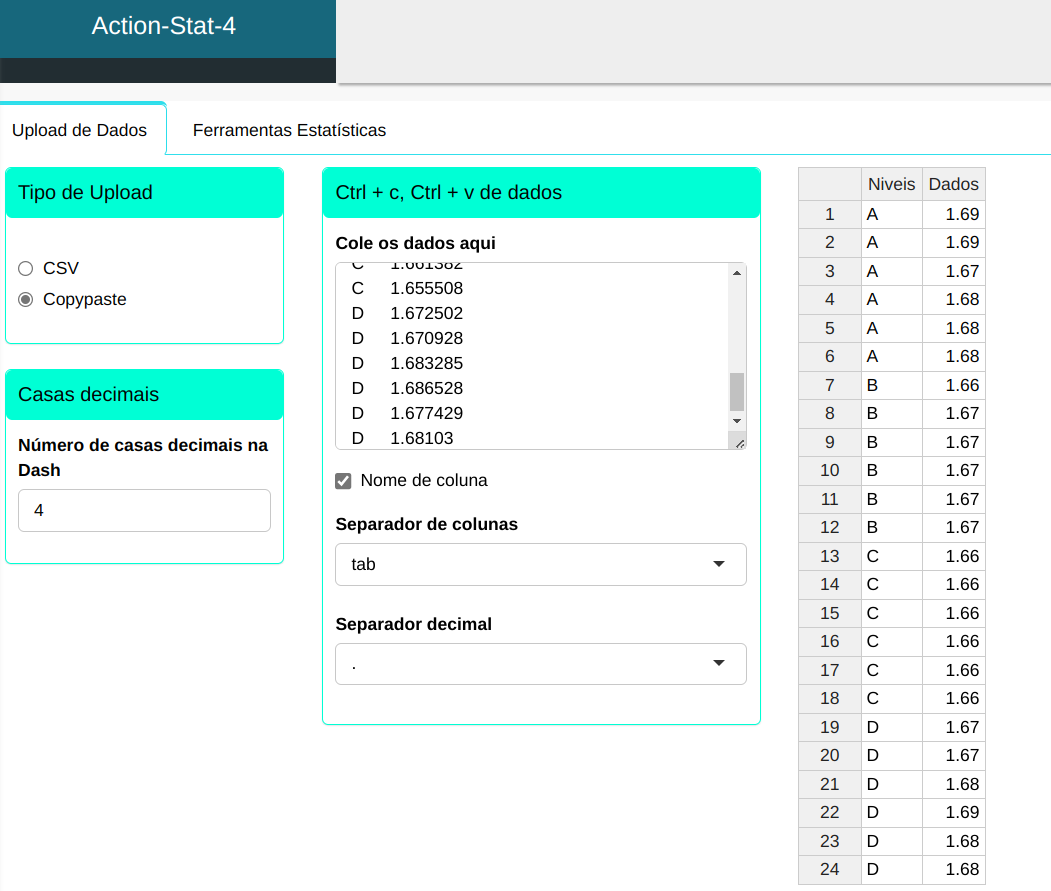
Configurando conforme a figura de abaixo para realizar o ressumo descritivo
Clique em Calcular para visualizar os resultados e baixá-los em formato Word.

Obtemos os seguintes resultados:
| Níveis | A | B | C | D |
|---|---|---|---|---|
| Mínimo | 1.672408 | 1.663774 | 1.655508 | 1.670928 |
| 1º Quartil | 1.6775395 | 1.6653895 | 1.65803925 | 1.67221085 |
| Média | 1.6814028 | 1.6678955 | 1.660201 | 1.678617 |
| Mediana | 1.681542 | 1.6676535 | 1.660895 | 1.6792295 |
| Tri- Média | 1.6814028 | 1.6678955 | 1.660201 | 1.678617 |
| 3º Quartil | 1.68620175 | 1.6708445 | 1.6622583 | 1.6840958 |
| Máximo | 1.688109 | 1.671857 | 1.663021 | 1.686528 |
| Soma | 10.088109 | 10.007373 | 9.961206 | 10.071702 |
| Soma Quadrática | 16.96284153 | 16.69130173 | 16.53764056 | 16.90671831 |
| Desvio Padrão da Média | 0.002225628 | 0.0012824453 | 0.00110154 | 0.00250414 |
| Desvio Padrão | 0.00545165 | 0.0031413367 | 0.00269823 | 0.006133873 |
| Variância | 0.00007972 | 0.00000987 | 0.00000728 | 0.00003762 |
| Coeficiente de Variação | 0.32423250 | 0.188341338 | 0.16252422 | 0.36541231 |
| Assimetria | -0.3740836 | -0.010343887 | -0.64230944 | -0.05347545 |
| Curtose | -1.3224643 | -1.94651104 | -1.22707584 | -1.90258576 |
| Amplitude | 0.015701 | 0.008083 | 0.007513 | 0.0156 |
| Tamanho da Amostra | 6 | 6 | 6 | 6 |
As médias e as medianas referentes a cada nível são representantes da distribuição global do diâmetro de peças medidas por cada um dos operadores.
-
A variabilidade resultante não é significativa.
-
A função de distribuição é mais achatada que a distribuição Normal, pois a Curtose é negativa em todos os níveis. Já, como o valor da Assimetria é também negativo em todos os níveis, a função de distribuição tem cauda levemente mais longa do lado esquerdo, ou seja, a distribuição é assimétrica à esquerda.