11. Teste de Equivalência
Com a ferramenta Teste de Equivalencia oferece análises para dados contínuos com variâncias iguais ou diferentes, e também oferece os testes de não inferioridade, de superioridade e de equivalência para dados binários.
Exemplo 1:
Neste exemplo deseja-se testar se uma nova metodologia é superior a metodologia compendial. Para isso, avalia-se a proporção de resultados positivos para ambos os métodos. Os dados resumidos são dados na Tabela a seguir.
| Resultados | Alternativo | Compendial |
|---|---|---|
| Positivo | 133 | 105 |
| Estéril | 17 | 45 |
| Total | 150 | 150 |
Realizaremos o teste no sistema. Configurando conforme a figura de abaixo.
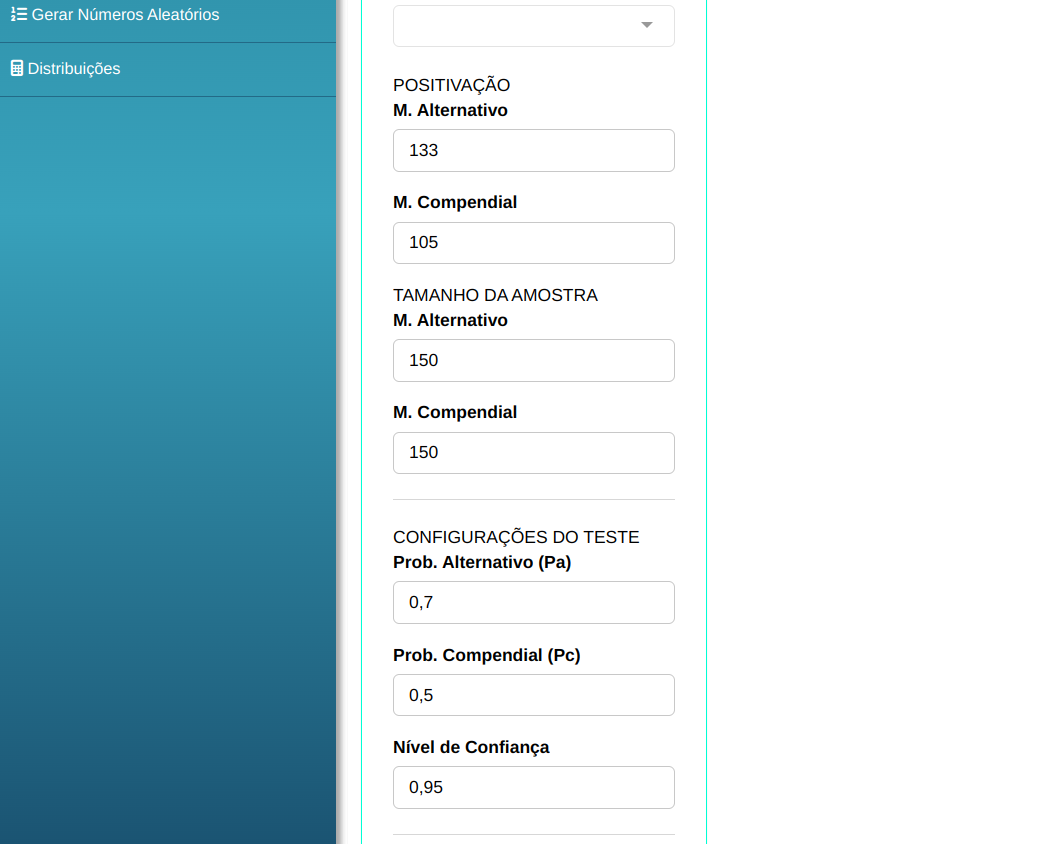
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Esta seção está baseada na norma United States Pharmacopeia [1], em que define a hipótese de Superioridade como a proporção de resultados positivos para o procedimento alternativo (PA) menos a proporção de resultados positivos para o procedimento tradicional ou compendial (PC), tem uma margem de tolerância de Superioridade (Delta = 0,2). A hipótese de Superioridade é dada por:
$$H_0: Pa-Pc \leq \Delta$$
$$H_1: Pa-Pc > \Delta$$
| Símbolo | Legenda/Fórmula |
|---|---|
| Na | Tamanho da Amostra do Método Alternativo |
| Nc | Tamanho da Amostra do Método Compendial |
| Xa | Quantidade de Positivações do Método Alternativo |
| Xc | Quantidade de Positivações do Método Tradicional |
| Pa | Proporção para o Método Alternativo |
| Pc | Proporção para o Método Compendial |
| ^Pa | Xa/Na |
| ^Pc | Xc/Nc |
| theta? | Nc/Na |
| R | Pa/Pc |
| a | 1+\theta |
| b | -[R(1+theta ^Pc)+theta+^Pa] |
| c | R(^Pa+theta ^Pc) |
| ~Pa | (-b-raiz(b²-4ac))/2a |
| ~Pc | ~Pa/R |
| V | [~Pa(1-~Pa)]/Na+R²[~Pc(1-~Pc)]/Nc |
| Z | (^Pa-R^Pc)/raiz(V) |
$\quad$ Resultados do Teste de Superioridade
Resultados do Método Compendial
| Quantidade | Proporção Estimada | |
|---|---|---|
| Positivo | 105 | 0.7 |
| Estéril | 45 | 0.3 |
| Total | 150 | 1.0 |
Resultados do Método Alternativo
| Quantidade | Proporção Estimada | |
|---|---|---|
| Positivo | 133 | 0.8866667 |
| Estéril | 17 | 0.1133333 |
| Total | 150 | 1.0000000 |
Parâmetros de teste:
$$H_0: Pa-Pc \leq \Delta$$ $$H_1: Pa-Pc > \Delta$$
| Valor | |
|---|---|
| Theta | 1.000000000 |
| Razão de Proporções (R) | 1.400000000 |
| a | 2.000000000 |
| b | -4.266666667 |
| c | 2.221333333 |
| ~pa | 0.902012146 |
| ~pc | 0.644294390 |
| Variância (V) | 0.003583849 |
| Raiz(V) | 0.059865256 |
| ^pa-R*^pc | -0.093333333 |
| Estatística Z | -1.559056788 |
Critério de Rejeição
| Valor | |
|---|---|
| Nível de significância | 0.0500000 |
| Quantil da Normal Padrão - Superioridade | 1.6448536 |
| P-Valor | 0.9405085 |
Intervalo de confiança
| Valor | |
|---|---|
| Nível de Confiança | 0.95 |
| Limite Superior | 0.261502 |
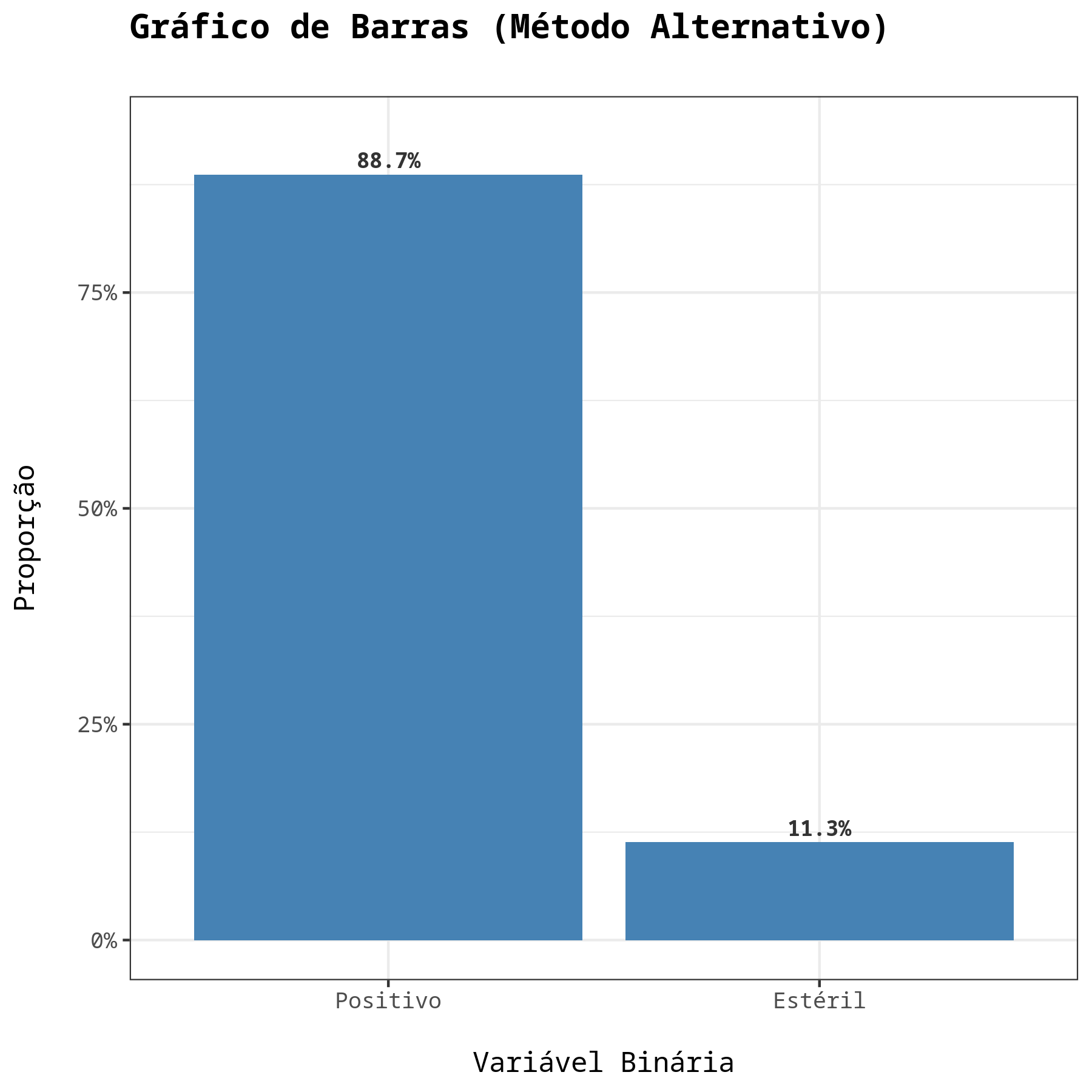
Dos resultados obtidos, não rejeitamos a hipótese nula, ao nível de significância de 5%. Portanto, concluímos que o método alternativo é não superior em relação ao método Tradicional.
Exemplo 2:
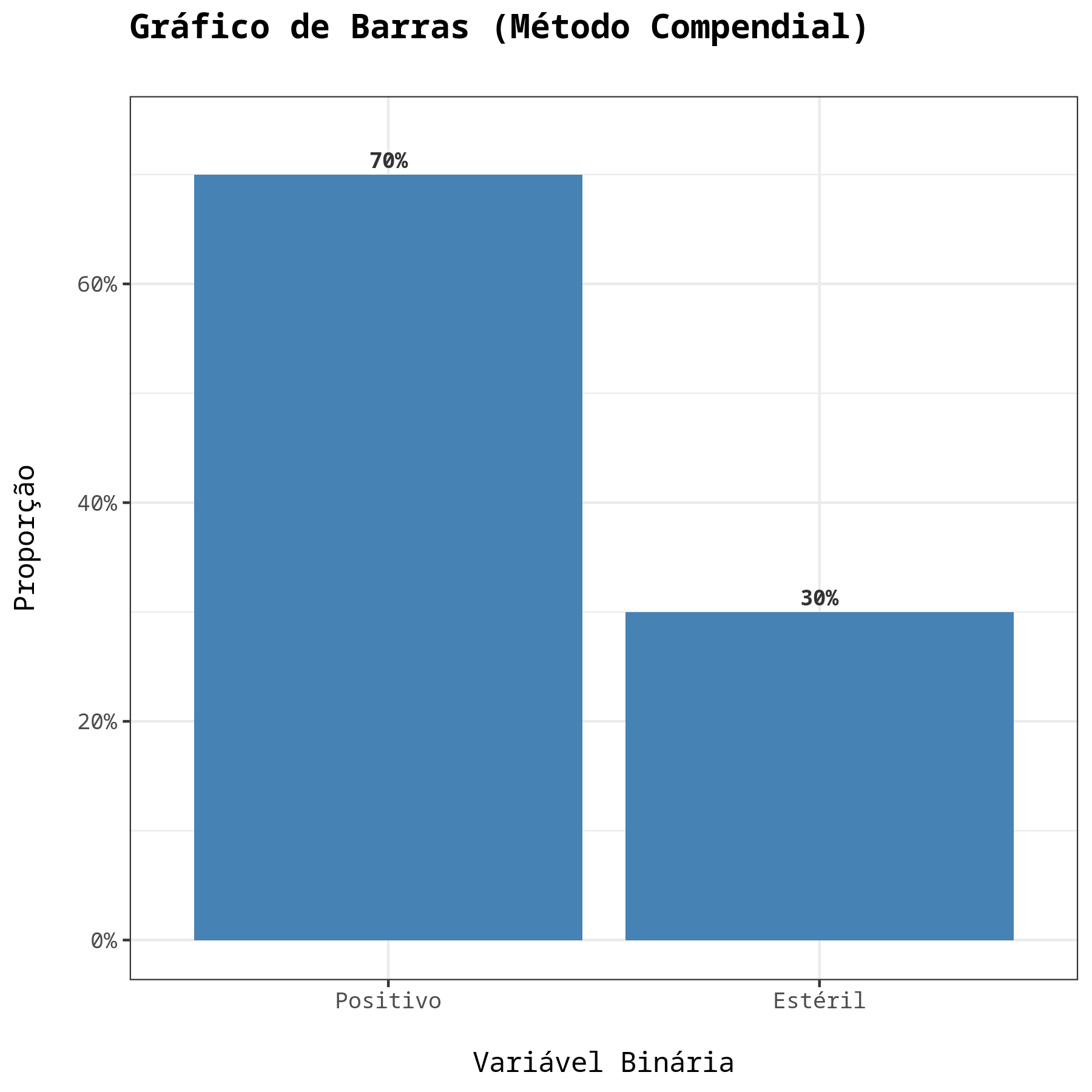
Neste exemplo deseja-se testar se uma nova metodologia é equivalente a metodologia compendial. Para isso, avalia-se a proporção de resultados positivos para ambos os métodos. Os dados resumidos sao dados na Tabela a seguir
| Resultados | Alternativo | Compendial |
|---|---|---|
| Positivo | 105 | 133 |
| Estéril | 45 | 17 |
| Total | 150 | 150 |
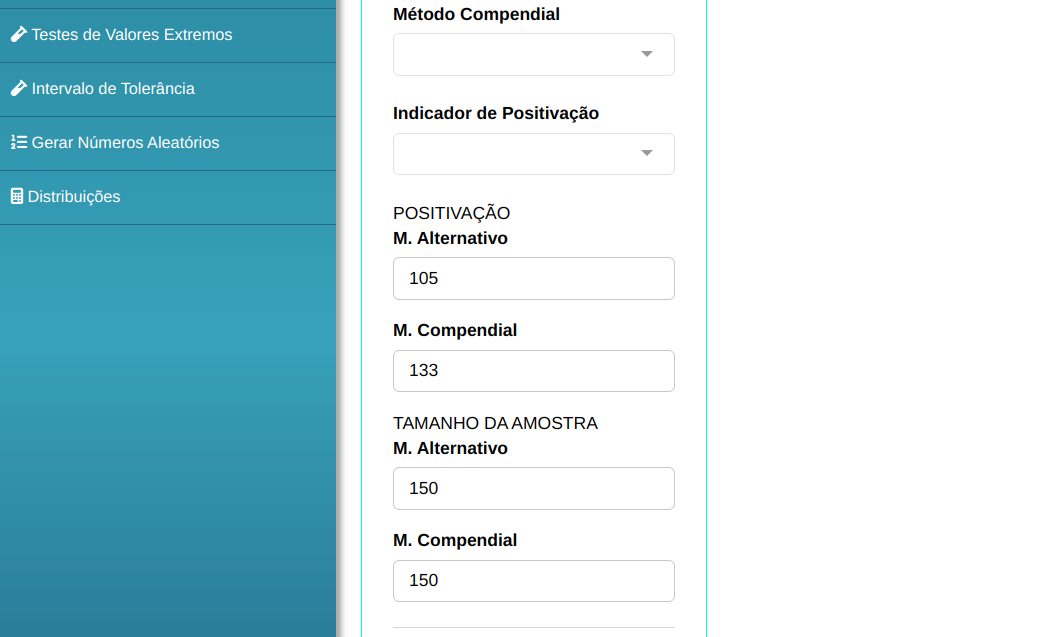
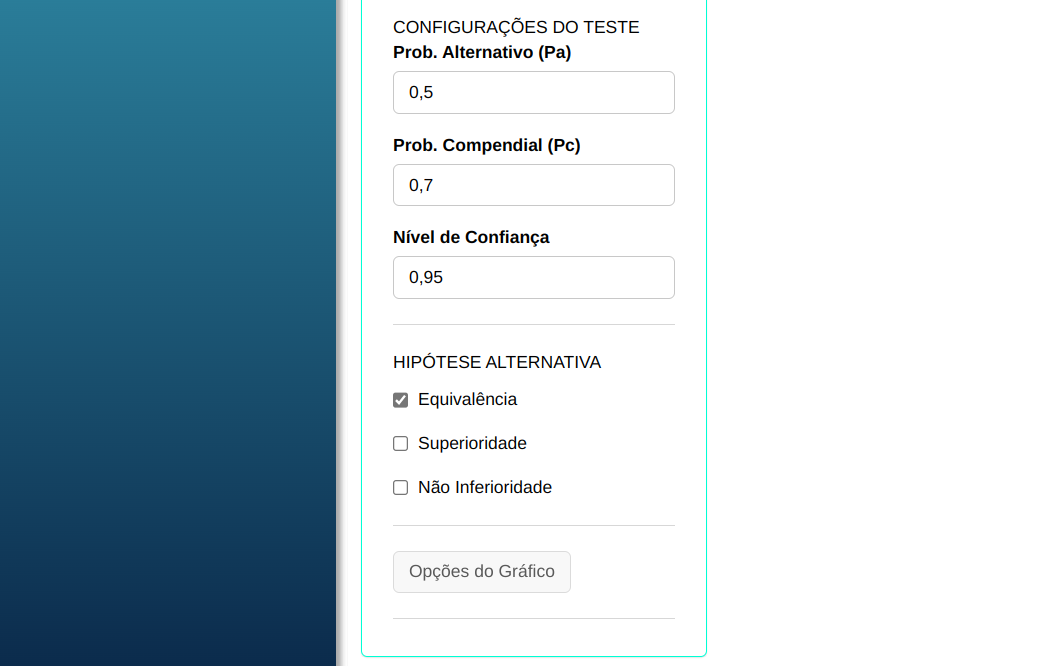
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Esta seção está baseada na norma United States Pharmacopeia [1], em que define a hipótese de Equivalência como a proporção de resultados positivos para o procedimento alternativo (PA) menos a proporção de resultados positivos para o procedimento tradicional ou compendial (PC), tem uma margem de tolerância de Equivalência (Delta = -0,2). A hipótese de Equivalência é dada por:
$$H_0: Pa-Pc \leq -\Delta \qquad \textrm{ou} \qquad Pa-Pc \geq \Delta$$
$$H_1: -\Delta < Pa-Pc < \Delta$$
| Símbolo | Legenda/Fórmula |
|---|---|
| Na | Tamanho da Amostra do Método Alternativo |
| Nc | Tamanho da Amostra do Método Compendial |
| Xa | Quantidade de Positivações do Método Alternativo |
| Xc | Quantidade de Positivações do Método Tradicional |
| Pa | Proporção para o Método Alternativo |
| Pc | Proporção para o Método Compendial |
| ^Pa | Xa/Na |
| ^Pc | Xc/Nc |
| theta? | Nc/Na |
| R | Pa/Pc |
| a | 1+theta |
| b | -[R(1+theta^Pc)+theta+^Pa] |
| c | R(^Pa+theta^Pc) |
| ~Pa | (-b-raiz(b²-4ac))/2a |
| ~Pc | ~Pa/R |
| V | [~Pa(1-~Pa)]/Na+R²[~Pc(1-~Pc)]/Nc |
| Z | (~Pa-R~Pa)/raiz(V) |
$\quad$ Resultados do Teste de Equivalência
Resultados do Método Compendial
| Quantidade | Proporção Estimada | |
|---|---|---|
| Positivo | 133 | 0.8866667 |
| Estéril | 17 | 0.1133333 |
| Total | 150 | 1.0000000 |
Resultados do Método Alternativo
| Quantidad | Proporção Estimada | |
|---|---|---|
| Positivo | 105 | 0.7 |
| Estéril | 45 | 0.3 |
| Total | 150 | 1.0 |
Parâmetros de teste
$$H_{01}: Pa-Pc \leq -\Delta$$
$$H_{11}: Pa-Pc > -\Delta$$
| Valor | |
|---|---|
| Theta | 1.000000000 |
| Razão de Proporções (R) | 0.714285714 |
| a | 2.000000000 |
| b | -3.047619048 |
| c | 1.133333333 |
| ~pa | 0.644294390 |
| ~pc | 0.902012146 |
| Variância (V) | 0.001828494 |
| Raiz(V) | 0.042760897 |
| ^pa-R*^pc | 0.066666667 |
| Estatística Z | 1.559056788 |
Parâmetros de teste
$$H_{01}: Pa-Pc \geq \Delta$$
$$H_{11}: Pa-Pc < \Delta$$
| Valor | |
|---|---|
| Theta | 1.000000000 |
| Razão de Proporções (R) | 1.400000000 |
| a | 2.000000000 |
| b | -4.341333333 |
| c | 2.221333333 |
| ~pa | 0.825946021 |
| ~pc | 0.589961444 |
| Variância (V) | 0.004119312 |
| Raiz(V) | 0.064181866 |
| ^pa-R*^pc | -0.541333333 |
| Estatística Z | -8.434365747 |
Critério de rejeição
| Valor | |
|---|---|
| Nível de significância | 0.05000000 |
| Quantil da Normal Padrão - Não inferioridade | 1.64485363 |
| Quantil da Normal Padrão - Superioridade | -1.64485363 |
| P-Valor | 0.05949147 |
Intervalo de Confiança
| Valor | |
|---|---|
| Nível de Confiança | 0.95 |
| Limite Inferior | -0.26150165 |
| Limite Superior | -0.11183168 |
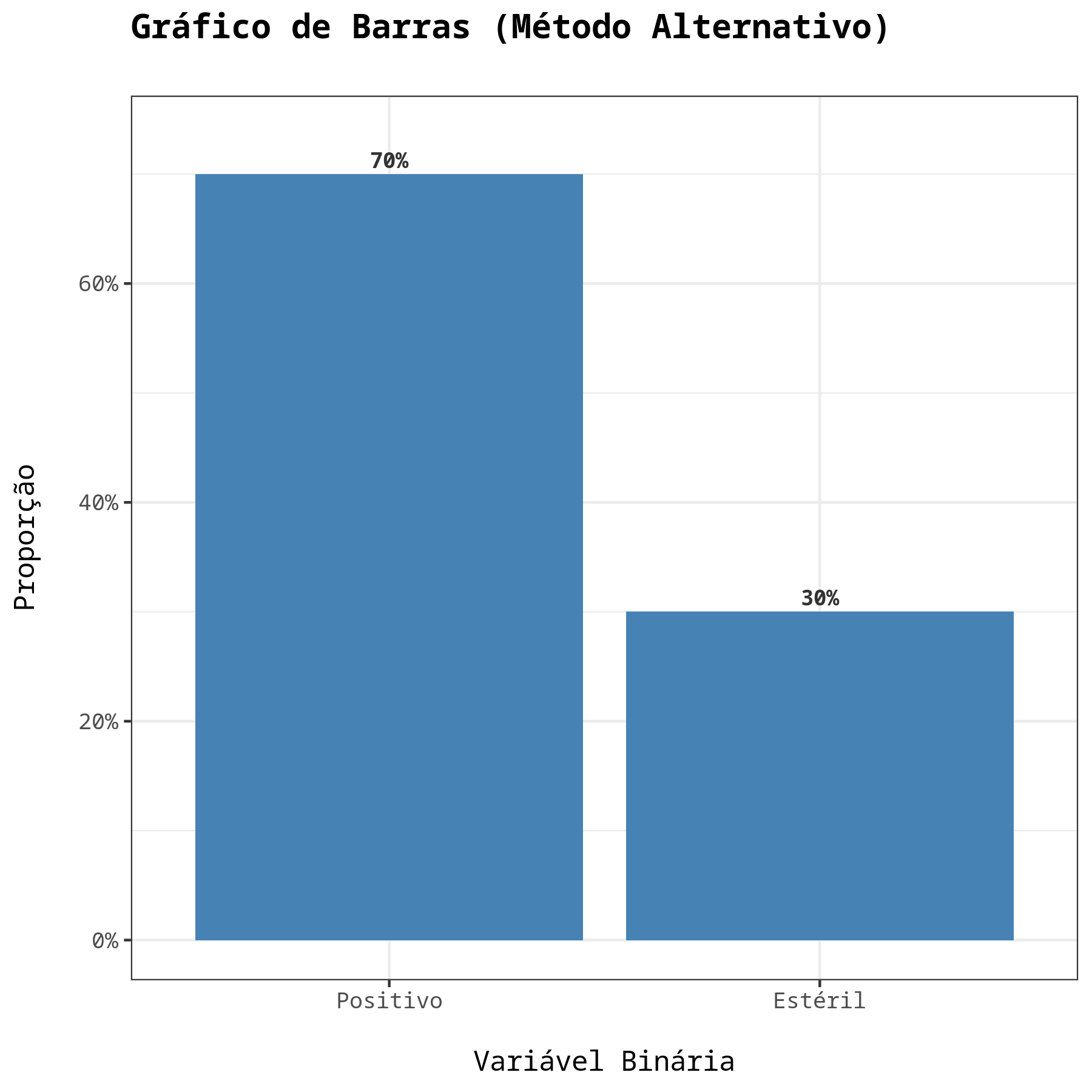
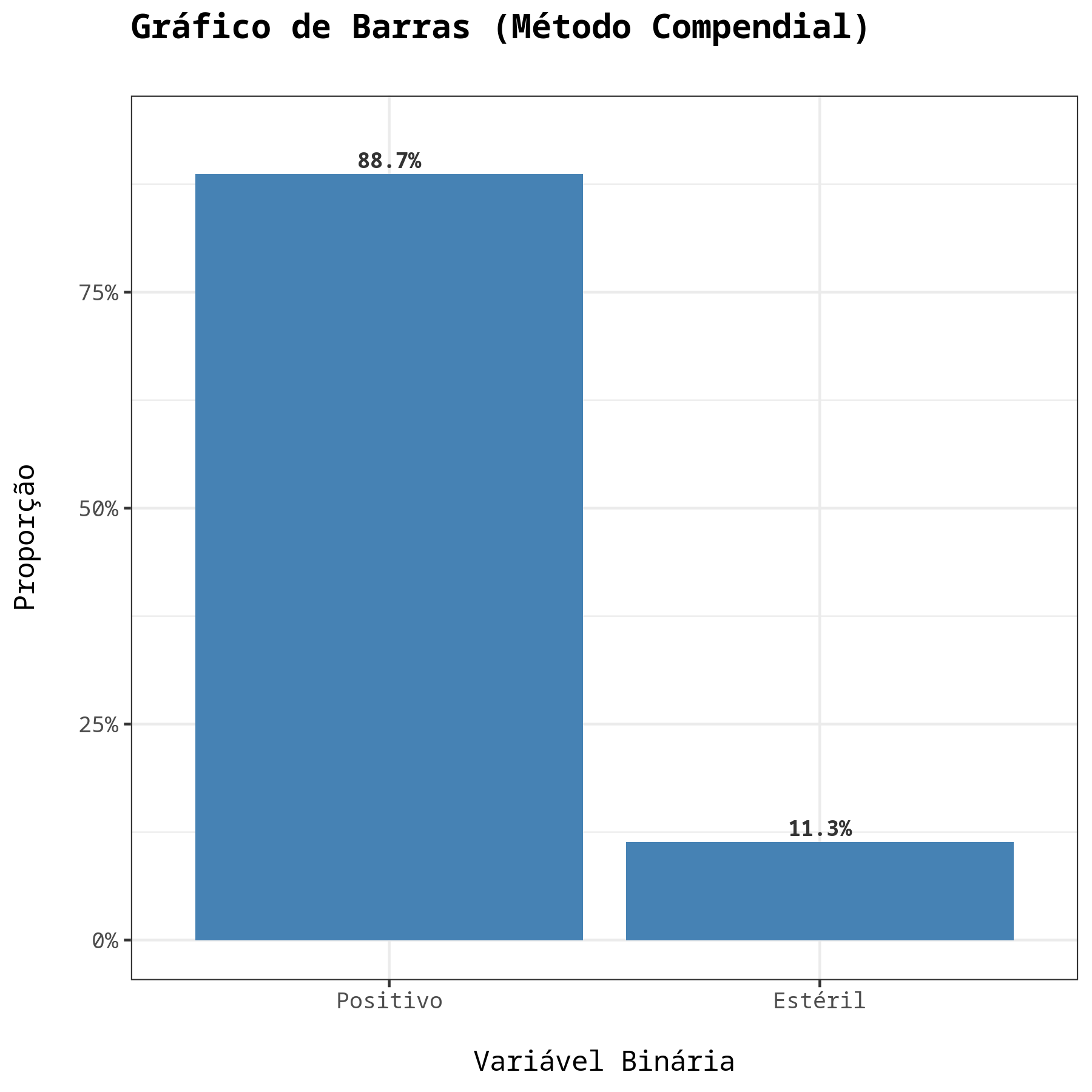
Dos resultados obtidos, não rejeitamos a hipótese nula, ao nível de significância de 5%. Portanto, concluímos pela Não Equivalência do método Alternativo em relação ao método Tradicional.
Exemplo 3:
Neste exemplo deseja-se testar se uma nova metodologia é não inferior a metodologia compendial. Para isso, avalia-se a proporção de resultados positivos para ambos os métodos. Os dados resumidos sao dados na Tabela a seguir.
| Resultados | Alternativo | Compendial |
|---|---|---|
| Positivo | 105 | 133 |
| Estéril | 45 | 17 |
| Total | 150 | 150 |
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Esta seção está baseada na norma United States Pharmacopeia [1], em que define a hipótese de Não Inferioridade como a proporção de resultados positivos para o procedimento alternativo (PA) menos a proporção de resultados positivos para o procedimento tradicional ou compendial (PC), tem uma margem de tolerância de Não Inferioridade (Delta = -0,2). A hipótese de Não Inferioridade é dada por:
$$H_0: Pa-Pc \leq -\Delta$$ e $$H_1: Pa-Pc > -\Delta$$
| Símbolo | Legenda-Fórmula |
|---|---|
| Na | Tamanho da Amostra do Método Alternativo |
| Nc | Tamanho da Amostra do Método Compendial |
| Xa | Quantidade de Positivações do Método Alternativo |
| Xc | Quantidade de Positivações do Método Tradicional |
| Pa | Proporção para o Método Alternativo |
| Pc | Proporção para o Método Compendial |
| ^Pa | Xa/Na |
| ^Pc | Xc/Nc |
| theta? | Nc/Na |
| R | Pa/Pc |
| a | 1+theta |
| b | -[R(1+theta ^Pc)+theta+^Pa] |
| c | R(^Pa+theta^Pc) |
| ~Pa | (-b-raiz(b²-4ac))/2a |
| ~Pc | ~Pa/R |
| V | [~Pa(1-~Pa)]/Na+R²[~Pc(1-~Pc)]/Nc |
| Z | (~Pa-R~Pa)/raiz(V) |
$\quad$ Resultados do Teste de Não Inferioridade
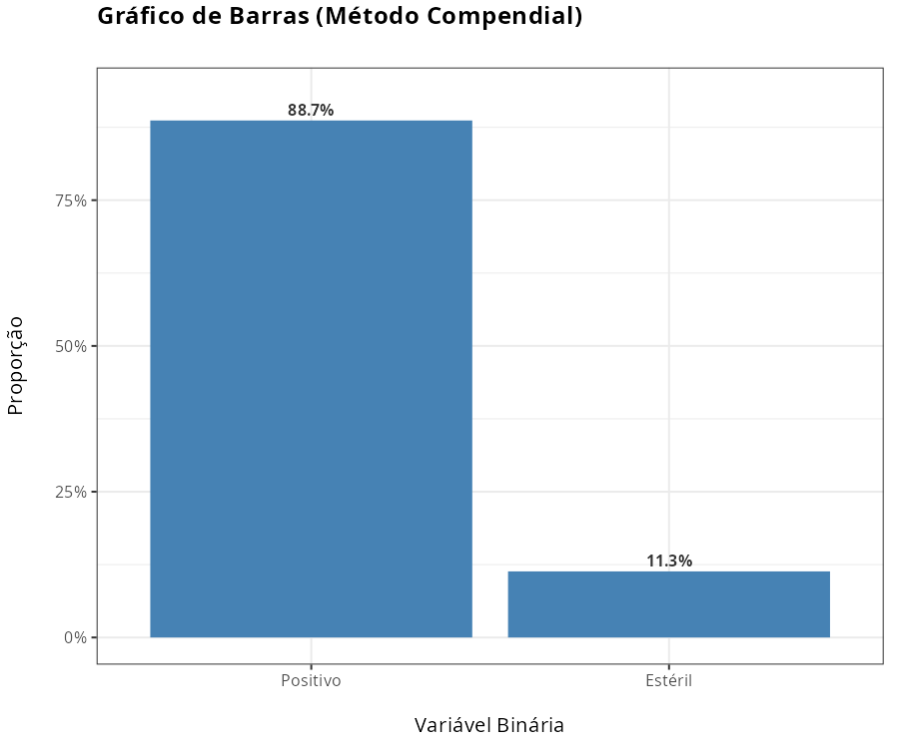
Resultado do Método Compendial
| Quantidade | Proporção Estimada | |
|---|---|---|
| Positivo | 133 | 0.8866667 |
| Estéril | 17 | 0.1133333 |
| Total | 150 | 1.0000000 |
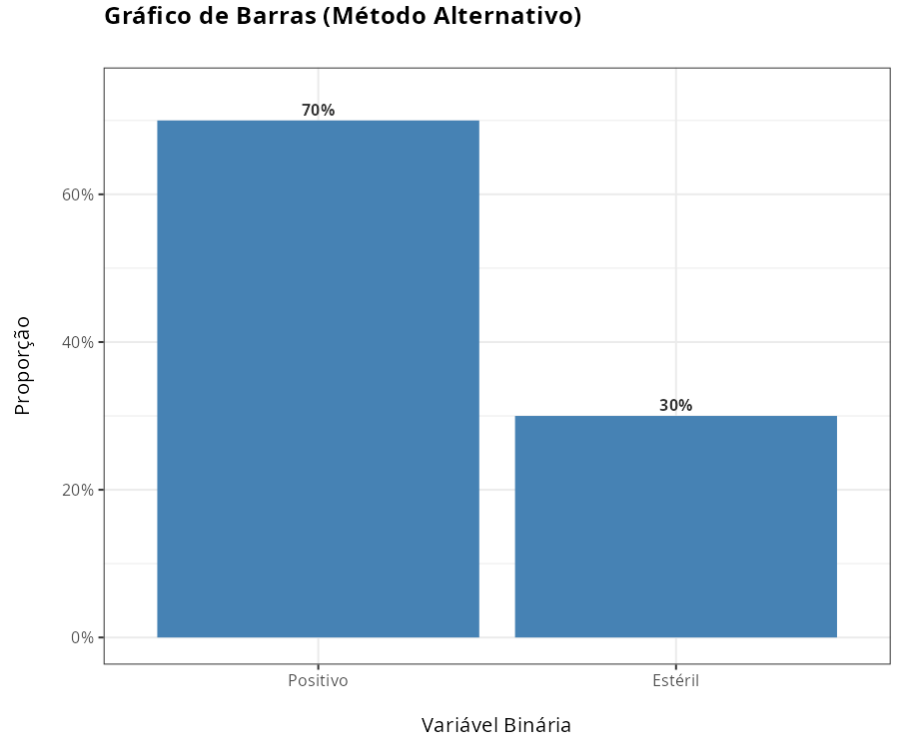
Resultado do Método Alternativo
| Quantidade | Proporção Estimada | |
|---|---|---|
| Positivo | 105 | 0.7 |
| Estéril | 45 | 0.3 |
| Total | 150 | 1.0 |
Parâmetros de teste
$$H_0: Pa-Pc \leq -\Delta$$
$$H_1: Pa-Pc > -\Delta$$
| Valor | |
|---|---|
| Theta | 1.000000000 |
| Razão de Proporções (R) | 0.714285714 |
| a | 2.000000000 |
| b | -3.047619048 |
| c | 1.133333333 |
| ~pa | 0.644294390 |
| ~pc | 0.902012146 |
| Variância (V) | 0.001828494 |
| Raiz(V) | 0.042760897 |
| ^pa-R*^pc | 0.066666667 |
| Estatística Z | 1.559056788 |
Critério de rejeição
| Valor | |
|---|---|
| Nível de significância | 0.05000000 |
| Quantil da Normal Padrão - Não inferioridade | 1.64485363 |
| P-Valor | 0.05949147 |
Intervalo de Confiança
| Valor | |
|---|---|
| Nível de Confiança | 0.95 |
| Limite Inferior | -0.26150165 |
Dos resultados obtidos, não rejeitamos a hipótese nula, ao nível de significância de 5%. Portanto, concluímos pela Inferioridade do método Alternativo em relação ao método Tradicional.
Exemplo 4:
Faremos o teste de equivalência para dados contı́nuos. Deseja-se testar a equivalência de dois laboratórios na concentração de um determinado medicamento, para isto foram coletadas 10 medicações de cada laboratório.
| Dados | Fator |
|---|---|
| 100,5449 | A |
| 99,67155 | A |
| 99,32921 | A |
| 100,0855 | A |
| 100,2163 | A |
| 100,0495 | A |
| 100,0238 | A |
| 99,28651 | A |
| 100,1467 | A |
| 99,72407 | A |
| 102,0206 | C |
| 101,0006 | C |
| 101,8330 | C |
| 101,7111 | C |
| 101,7244 | C |
| 98,65855 | C |
| 100,3181 | C |
| 100,9711 | C |
| 99,16993 | C |
| 100,7830 | C |
Faremos o upload dos dados no sistema.
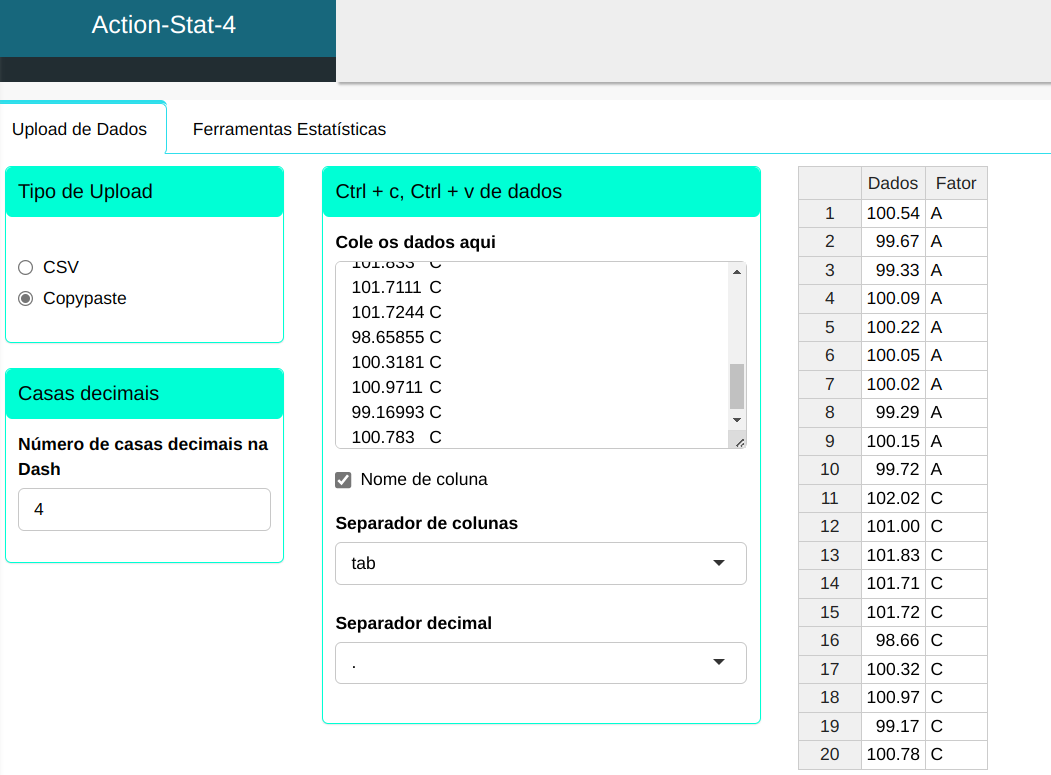
Realizaremos o teste.
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Avaliação da Equivalência
Para realizar o teste de equivalência, realizamos um teste t com as seguintes hipóteses:
$$H_0: m1-m2 \leq -d \qquad \textrm{ou} \qquad m1-m2 \geq d$$
vs
$$H_1: -d < m1-m2 < d$$
As quais podem ser escritas como:
$$H_{01}: m1-m2 \leq -d \quad \textrm{e} \quad H_{11}: m1-m2 \geq -d$$
$$H_{02}: m1-m2 \geq d \quad \textrm{e} \quad H_{12}: m1-m2 < d$$
Resultados
| Valores | |
|---|---|
| Graus de Liberdade | 11.1581 |
| P-valor | 0.4107 |
| Média - A | 99.9078 |
| Média - C | 100.8190 |
| Desvio Padrão - A | 0.3991 |
| Desvio Padrão - C | 1.1442 |
| Tamanho Amostral - A | 10.0000 |
| Tamanho Amostral - C | 10.0000 |
| Nível de Confiança | 0.9500 |
| Limite Inferior | -1.5985 |
| Limite Superior | -0.2239 |
| Margem de equivalência | 1.0000 |
| Estatística de Test 1 - $H_{01}: m1-m2 \leq -d$ | 0.2316 |
| Estatística de Test 2 - $H_{02}: m1-m2 \geq d$ | 4.9874 |
Para um nível de significância de 0,05 não rejeitamos a hipótese nula, isto é, concluímos que as características testadas não são equivalentes com um nível de significância de 5%.
Os resultados do Teste de Variância são apresentados na tabela.
| Amostra | Grupos |
|---|---|
| 100.5449 | A |
| 99.6716 | A |
| 99.3292 | A |
| 100.0855 | A |
| 100.2163 | A |
| 100.0495 | A |
| 100.0238 | A |
| 99.2865 | A |
| 100.1467 | A |
| 99.7241 | A |
| 102.0206 | C |
| 101.0006 | C |
| 101.8330 | C |
| 101.7111 | C |
| 101.7244 | C |
| 98.6586 | C |
| 100.3181 | C |
| 100.9711 | C |
| 99.1699 | C |
| 100.7830 | C |
Teste para Duas Variâncias
| Valores | |
|---|---|
| Estatística F | 0.121667 |
| Graus de liberdade (Numerador) | 9 |
| Graus de liberdade (Denominador) | 9 |
| P-Valor | 0.00436814 |
| Desvio padrão - A | 0.3991091 |
| Desvio padrão - C | 1.144208 |
| Tamanho de A | 10 |
| Tamanho de C | 10 |
| Hipótese Alternativa Diferente de | 1 |
| Intervalo de Confiança para razão das Variâncias | 95% |
| Limite Inferior | 0.03022037 |
| Limite Superior | 0.4898308 |
Em seguida, apresentamos o gráfico contendo o intervalo de confiança e a margem de equivalência.
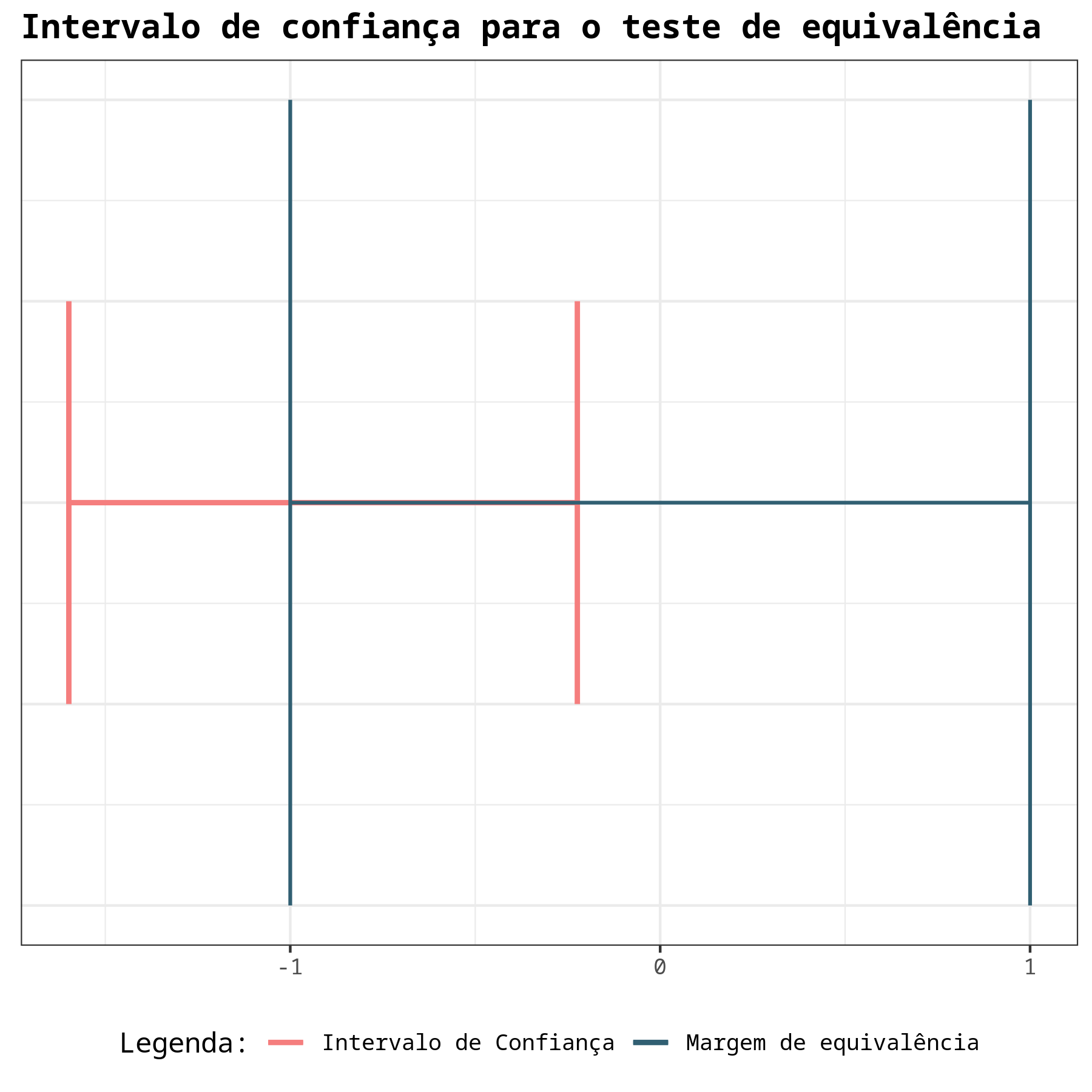
Com o P-valor > $\alpha$, não se rejeita a hipótese nula. Assim concluise que os laboratórios não são equivalentes ao nível de significância $\alpha$ = 5%