5. Teste de Normalidade
Os Testes de Normalidade são usados para determinar se um vetor numérico provém de uma Distribuição Normal.
Detalhes:
A ferramenta testes de normalidade permite determinar se um conjunto de dados é bem modelado por uma distribuição Normal, através dos testes de Anderson-Darling, Kolmogorov-Smirnov, Shapiro-Wilk ou Ryan-Joiner. Além dos testes a ferramenta gera o papel de probabilidade, que permite analisar de forma visual a normalidade dos dados.
Exemplo:
Quer se saber se o peso de certas peças segue uma distribuição normal. Para isto, uma amostra com 11 medidas de peso de peças (em pounds) foi obtida.
| Dados |
|---|
| 148 |
| 154 |
| 158 |
| 160 |
| 161 |
| 162 |
| 166 |
| 170 |
| 182 |
| 195 |
| 236 |
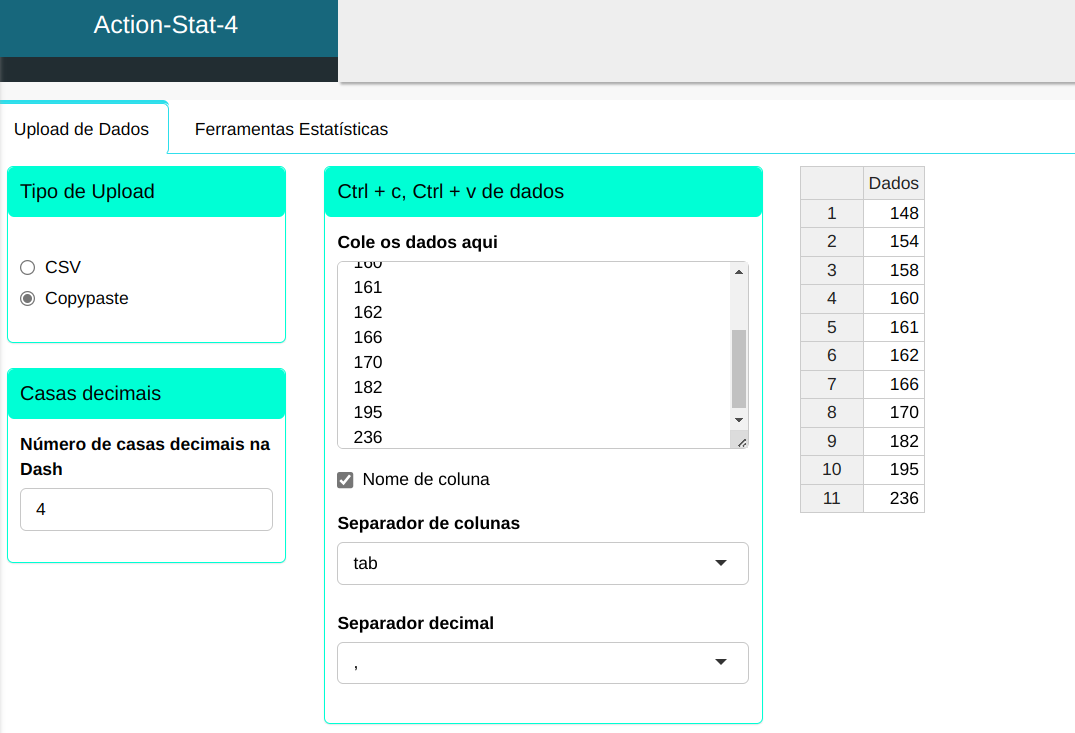
Faremos então o upload dos dados no sistema.
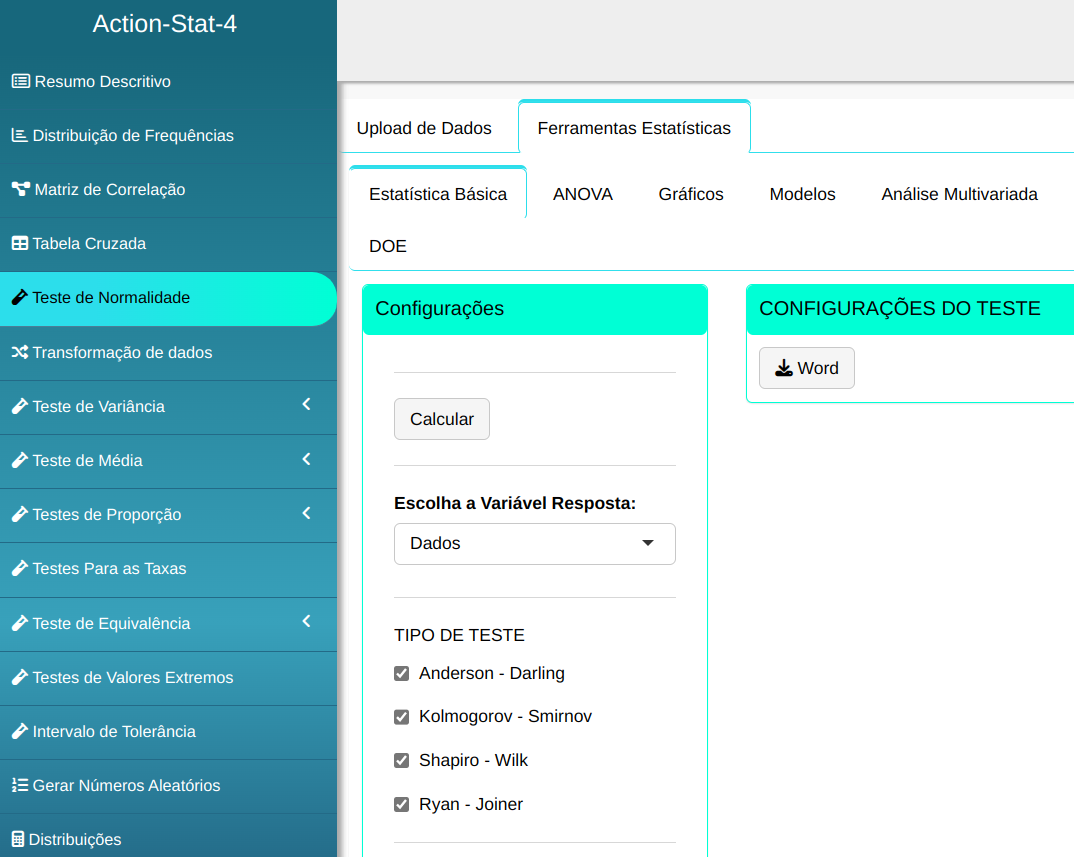
O teste de normalidade. é elaborado, conforme a configuração apresentada na figura abaixo.
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados obtidos são.
Testes de Normalidade
| Estatísticas | P-valores | |
|---|---|---|
| Anderson- Darling | 0.947 | 0.0105 |
| Kolmogorov- Smirnov | 0.259 | 0.0374 |
| Shapiro- Wilk | 0.789 | 0.0067 |
| Ryan- Joiner | 0.878 | 0.0089 |
Outliers (Quantis)
| Obs. | Quantis da Normal | Dados | Critério |
|---|---|---|---|
| 10 | 1.10 | 195 | Envelope (Nível de Confiança=95%) |
| 11 | 1.69 | 236 | Envelope (Nível de Confiança=95%) |


Como os P-valores são menores que 5%, para todos os testes, rejeitamos a hipótese de normalidade. Assim, com nível de confiança de 95%, temos evidências de que os dados não seguem uma distribuição normal.
O gráfico Papel de Probabilidade e o QQ-plot mostram que os dados não seguem uma distribuição normal, pois não estão alinhados sobre a reta. Dessa forma, conclui-se que o conjunto de dados não apresenta distribuição normal.