2. Teste de média: Duas amostras independentes
O teste t pode ser usado para comparar as médias de duas amostras independentes.
Exemplo 1:
Queremos testar a igualdade das médias de duas populações que tem variâncias iguais. Uma amostra de cada população foi obtida, conforme as Tabelas a seguir.
| Grupos | Amostra |
|---|---|
| População 1 | 18,8 |
| População 1 | 20,504 |
| População 1 | 18,621 |
| População 1 | 19,919 |
| População 1 | 21,117 |
| População 1 | 17,591 |
| População 1 | 18,756 |
| População 1 | 18,977 |
| População 1 | 20,308 |
| População 1 | 18,899 |
| População 1 | 20,835 |
| População 1 | 17,527 |
| População 1 | 17,078 |
| População 1 | 17,62 |
| População 1 | 21,426 |
| População 1 | 19,169 |
| População 1 | 19,29 |
| População 1 | 22,059 |
| População 1 | 18,585 |
| População 1 | 17,89 |
| População 1 | 18,755 |
| População 1 | 19,203 |
| População 1 | 18,419 |
| População 1 | 20,764 |
| População 1 | 21,055 |
| População 2 | 22,284 |
| População 2 | 21,901 |
| População 2 | 25,302 |
| População 2 | 22,447 |
| População 2 | 22,771 |
| População 2 | 22,057 |
| População 2 | 22,881 |
| População 2 | 17,968 |
| População 2 | 23,382 |
| População 2 | 21,043 |
| População 2 | 22,629 |
| População 2 | 22,86 |
| População 2 | 24,515 |
| População 2 | 22,426 |
| População 2 | 21,203 |
| População 2 | 24,62 |
| População 2 | 22,058 |
| População 2 | 23,15 |
| População 2 | 22,787 |
| População 2 | 24,009 |
| População 2 | 21,491 |
| População 2 | 22,699 |
| População 2 | 24,662 |
| População 2 | 21,983 |
| População 2 | 21,917 |
| População 2 | 21,198 |
| População 2 | 22,909 |
| População 2 | 23,327 |
| População 2 | 24,534 |
| População 2 | 21,152 |
Faremos o upload de dados no sistema.
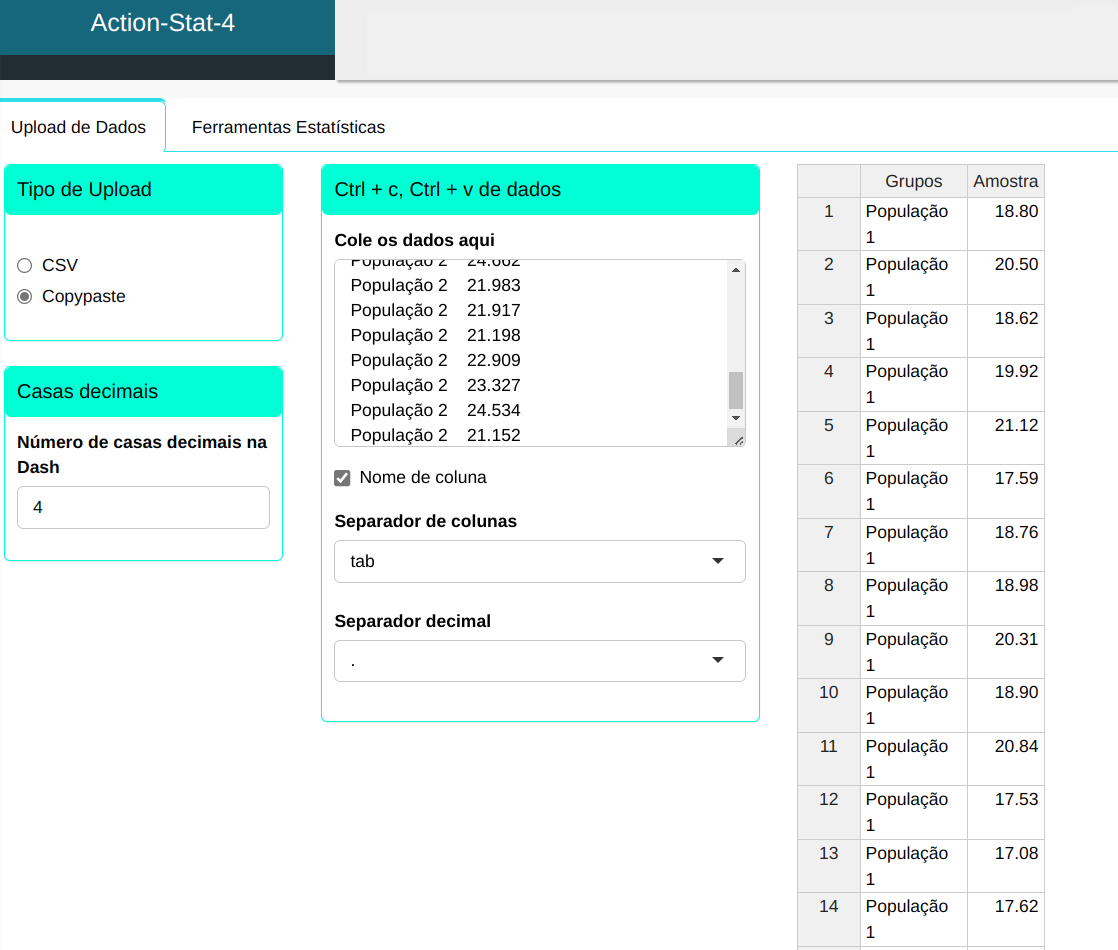
O teste é elaborado, conforme a configuração apresentada na figura de abaixo.
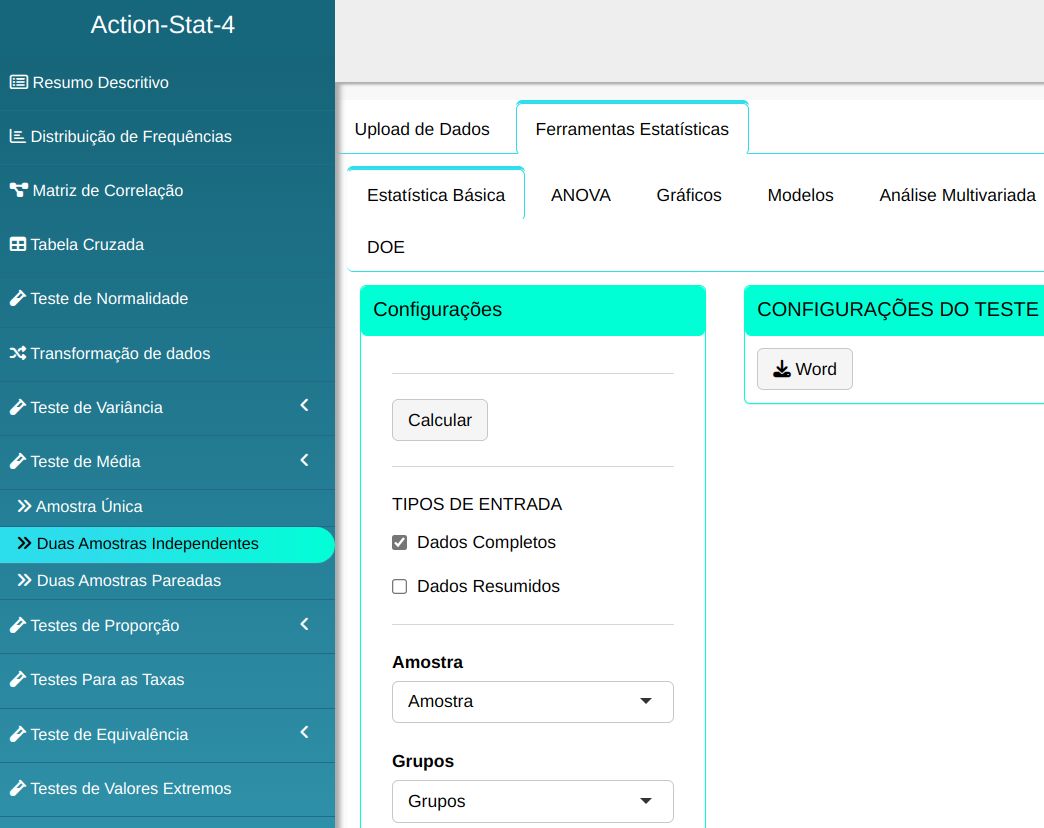
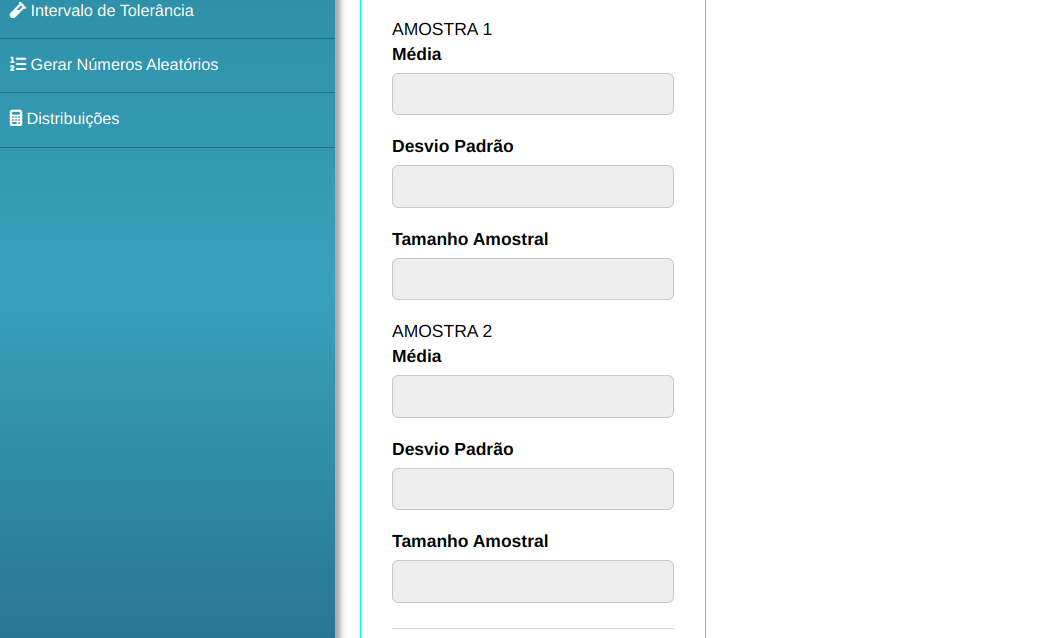
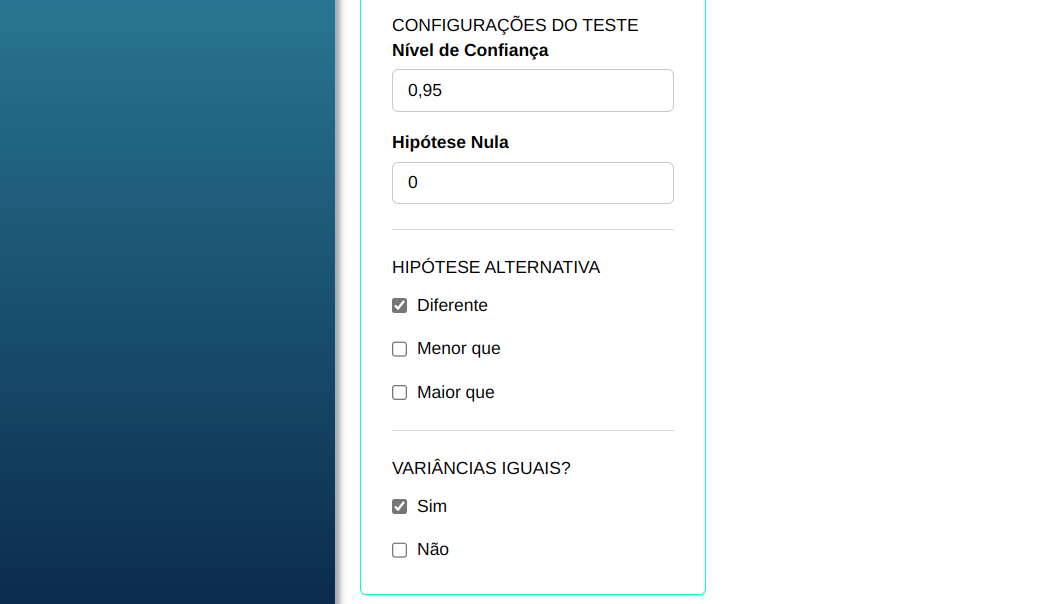
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Resultados
| Valores | |
|---|---|
| Estatística T | -8.621733 |
| Graus de Liberdade | 53 |
| P-valor | 1.151931e-11 |
| Média da População 1 | 19.32668 |
| Média da População 2 | 22.6055 |
| Desvio Padrão da População 1 | 1.362278 |
| Desvio Padrão da População 2 | 1.43822 |
| Desvio Padrão Agrupado | 1.40434 |
| Tamanho da População 1 | 25 |
| Tamanho da População 2 | 30 |
| Hipótese Alternativa Diferente de | 0 |
| Nível de Confiança | 95% |
| Limite Inferior | -4.041599 |
| Limite Superior | -2.516041 |
A estatística do teste é -8,62. Como o p-valor é 1,15193E-11, então ao nível de significância de 5%, rejeitamos a hipótese nula de igualdade das médias das duas populações.
Exemplo 2:
Queremos testar a igualdade das médias de duas populações que tem variâncias iguais. Uma amostra de cada população foi obtida, conforme as Tabelas a seguir.
| Médias | Desvio Padrão | Tamanho da amostra | |
|---|---|---|---|
| Amostra 1 | 19,32668 | 1,362277802 | 25 |
| Amostra 2 | 22,6055 | 1,438220326 | 30 |
O teste é elaborado, conforme a configuração apresentada na figura de abaixo.
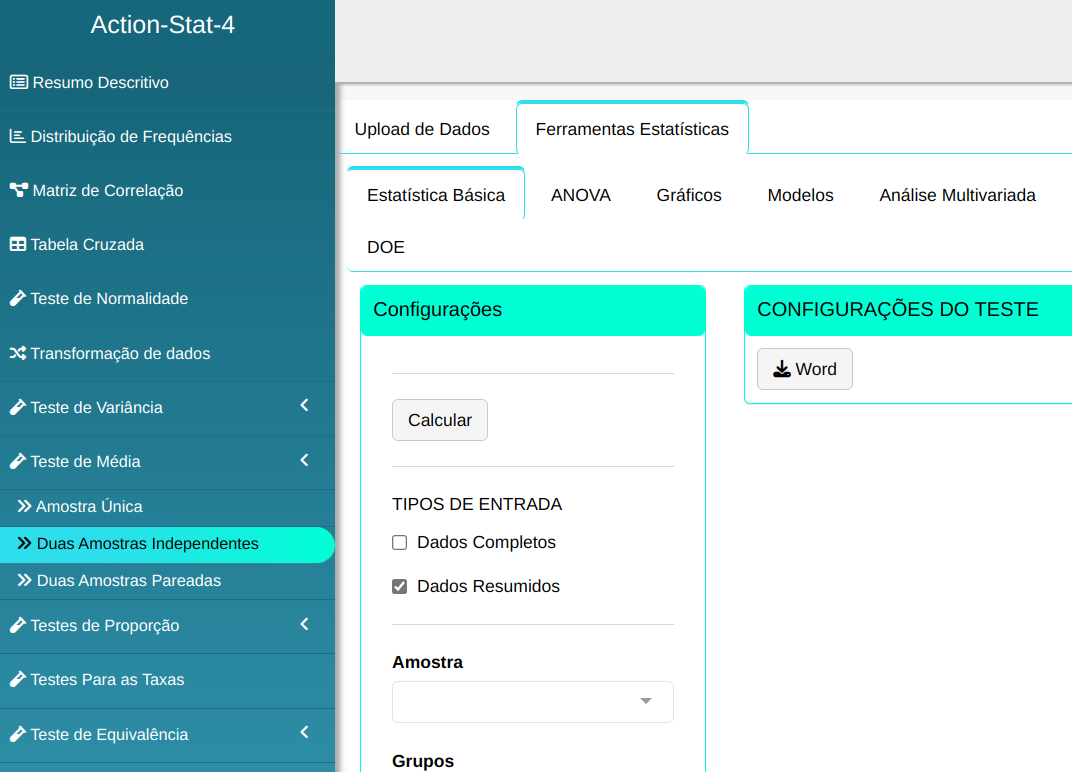
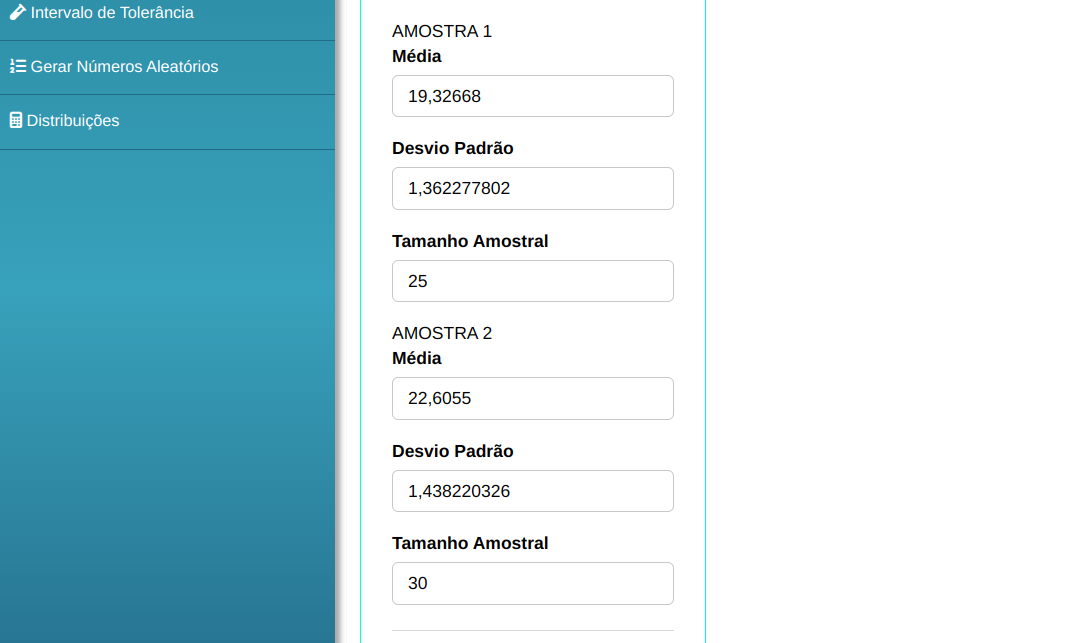
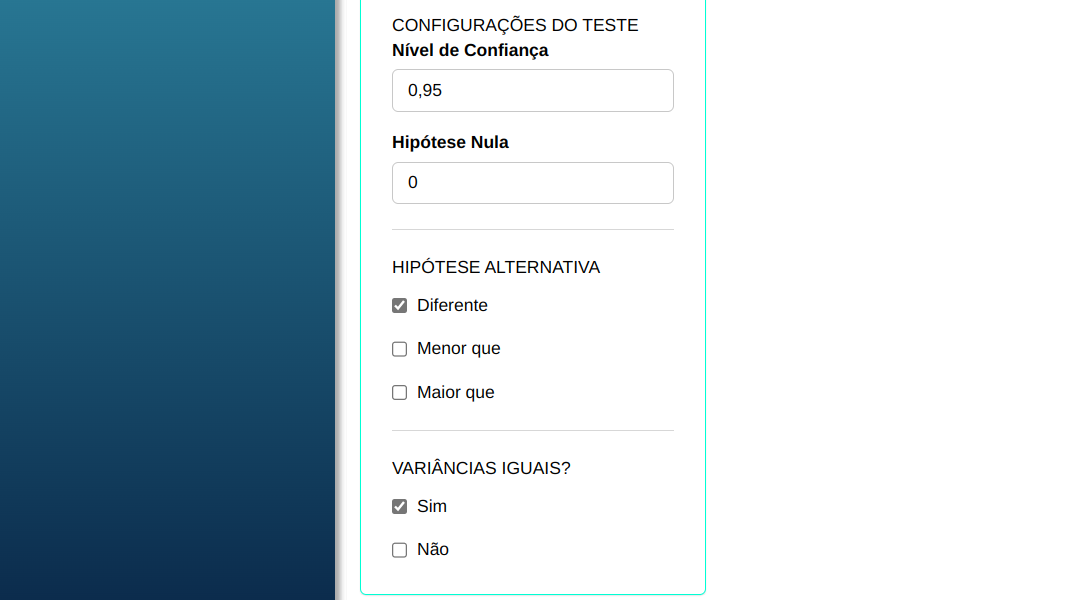
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Resultados
| Valores | |
|---|---|
| Estatística T | -8.621733 |
| Graus de Liberdade | 53 |
| P-valor | 1.151931e-11 |
| Média da Amostra 1 | 19.32668 |
| Média da Amostra 2 | 22.6055 |
| Desvio Padrão da Amostra 1 | 1.362278 |
| Desvio Padrão da Amostra 2 | 1.43822 |
| Desvio Padrão Agrupado | 1.40434 |
| Tamanho da Amostra 1 | 25 |
| Tamanho da Amostra 2 | 30 |
| Hipótese Alternativa Diferente de | 0 |
| Nível de Confiança | 95% |
| Limite Inferior | -4.041599 |
| Limite Superior | -2.516041 |
A estatística do teste é -8,62. Como o p-valor é 1,15E-11 então ao nível de significância de 5%, rejeitamos a hipótese nula de igualdade das médias das duas populações.