3. Teste de média: duas amostras pareadas
O teste T pareado verificará a média das diferenças entre duas amostras independentes.
Exemplo:
Consideremos uma amostra de medições do laboratório da Empresa A e uma amostra de medições do laboratório da Empresa B, valores que se encontram na Tabela a seguir. Os testes dos dois laboratórios são realizadas no mesmo padrão, por isso, existe uma correlação entre eles, ou seja, as amostras são dependentes. Avalie a compatibilidade das medições entre o laboratório da empresa A e do laboratório da empresa B.
| LAB A | LAB B |
|---|---|
| 1.00552 | 0.01942 |
| -1.49928 | -0.46512 |
| 0.21367 | 0.53218 |
| 0.44658 | -0.14844 |
| 0.62766 | -0.60021 |
| 0.31091 | 0.06495 |
| -0.83878 | 0.33013 |
| -0.29054 | 0.12116 |
| -0.08487 | 0.74269 |
| -1.26465 | -1.64232 |
| -0.06353 | 0.05497 |
| -1.07632 | 0.76342 |
| -1.34134 | 1.74131 |
| -0.55062 | -0.06392 |
| 1.61848 | -1.88146 |
| 0.50997 | -0.76135 |
| 0.76027 | -0.23009 |
| 0.68061 | -1.16800 |
| -1.91464 | 0.88392 |
| -0.20072 | 0.96512 |
Faremos o upload dos dados no sistema.
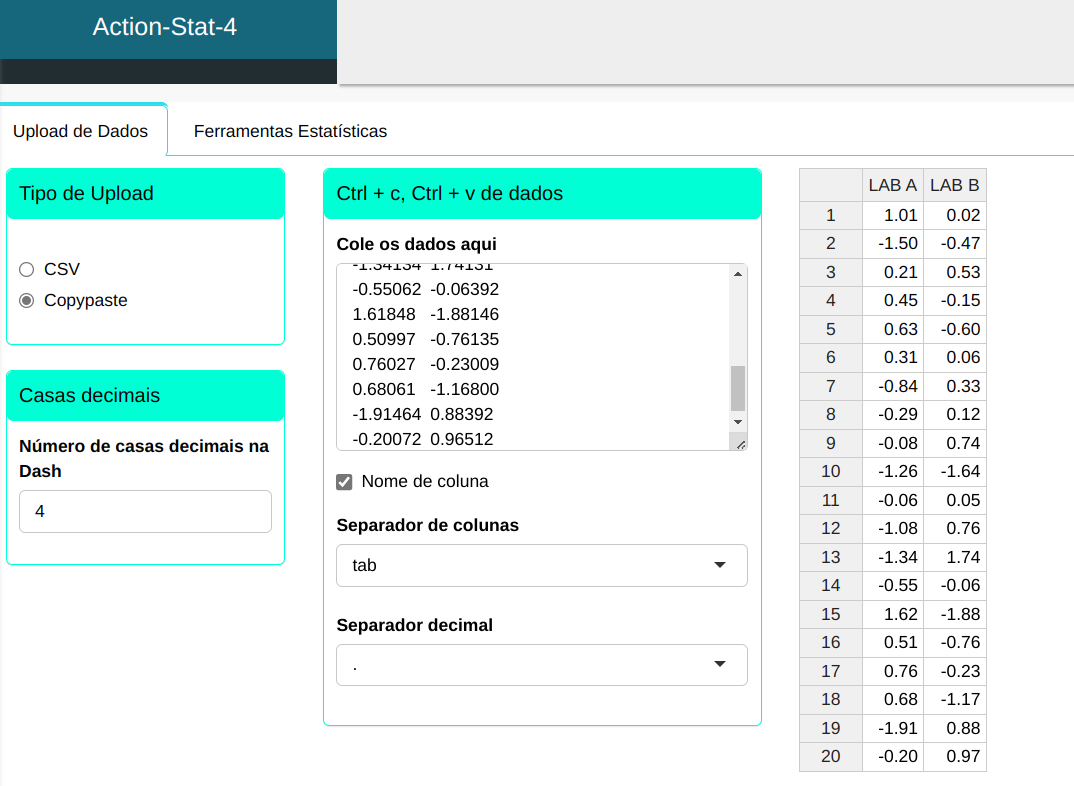
Realizaremos então o teste.
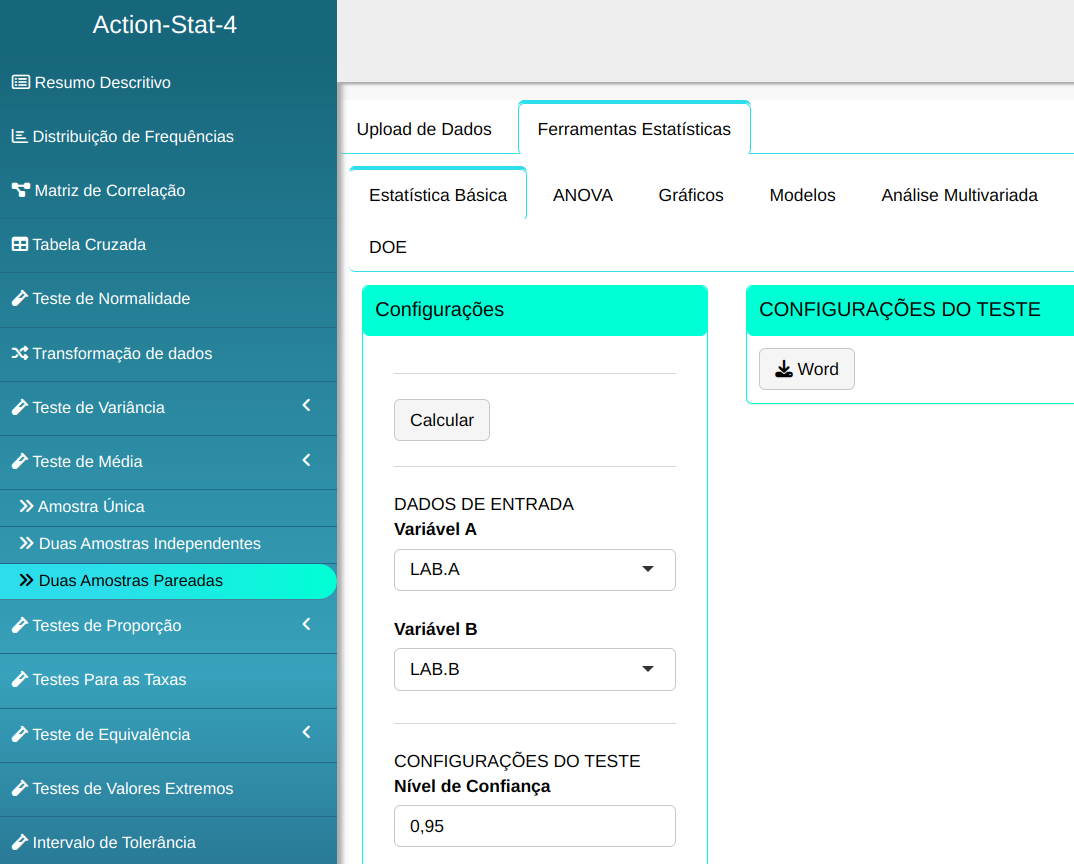
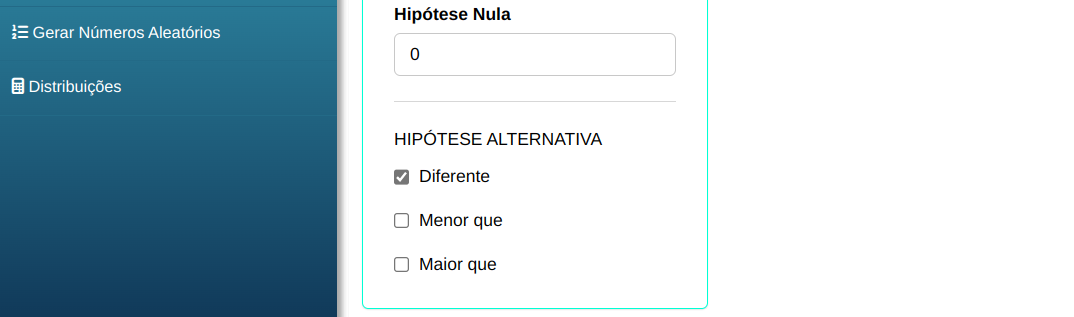
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Resultados
| Valores | |
|---|---|
| Estatística T | -0.3149009 |
| Graus de Liberdade | 19 |
| P-valor | 0.756269 |
| Média de LAB.A | -0.14757 |
| Média de LAB.B | -0.037085 |
| Desvio Padrão das diferenças | 1.569077 |
| Tamanho das Amostras | 20 |
| Hipótese Alternativa Diferente de | 0 |
| Nível de Confiança | 95% |
| Limite Inferior | -0.8448358 |
| Limite Superior | 0.6238658 |
A estatística do teste é -0,3149887. Como o p-valor é 0,7562 então, a um nível de significância de 5%, não rejeitamos a hipótese nula de compatibilidade das medições entre o laboratório da empresa A e o laboratório da empresa B.