1. Proporções: amostra única
Teste de proporções é usado para analisar se a taxa de sucesso de um experimento é satisfatória.
Exemplo 1:
Um fabricante garante que 90% das peças que fornece à linha de produção de uma determinada fábrica concorda com as especificações exigidas. Foi selecionada uma amostra de 200 peças e cada peça foi avaliada como dentro das especificações (valor 1) ou fora das especificações (valor 0) segundo a tabela abaixo. A um nível de 5%, podemos dizer que é verdadeira a afirmação do fabricante?
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 0 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
| 0 |
| 0 |
| 1 |
Faremos então o Upload dos dados no sistema.
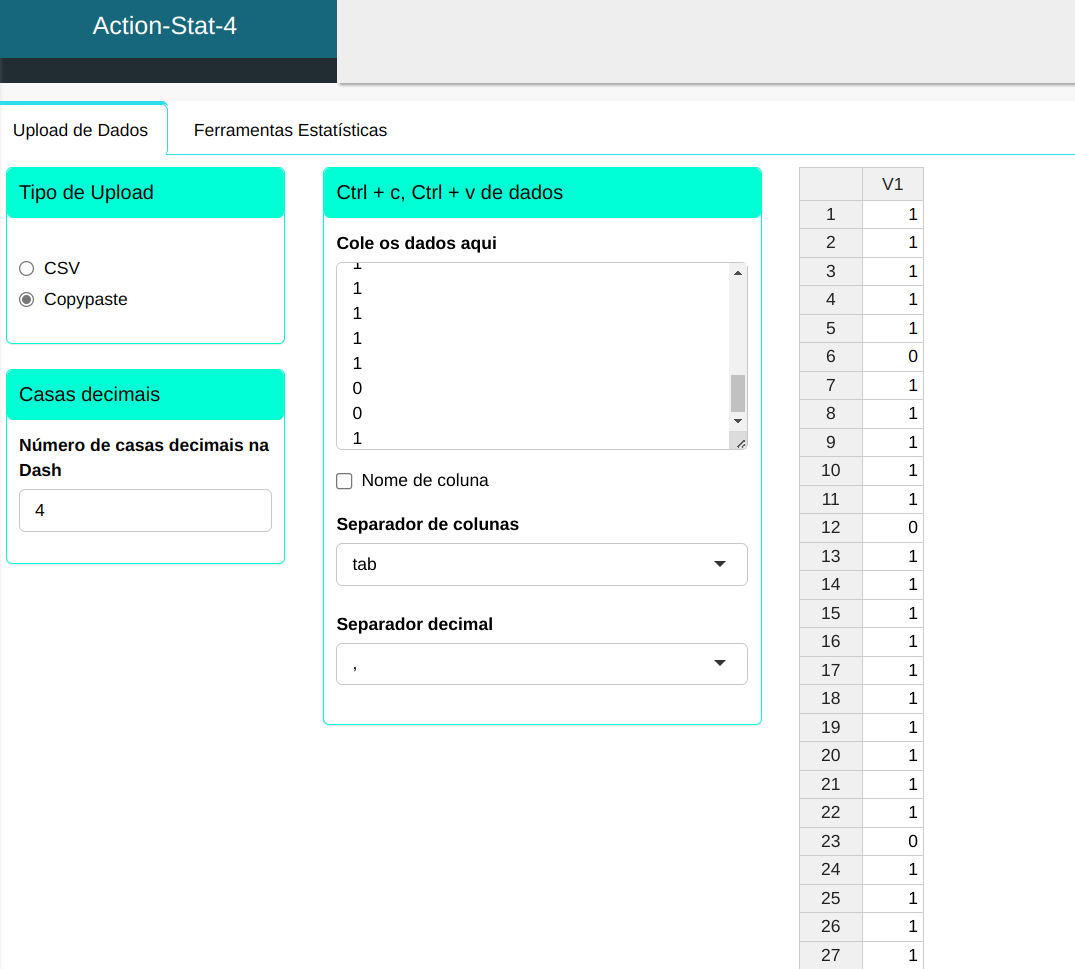
Faremos o Teste de proporção.
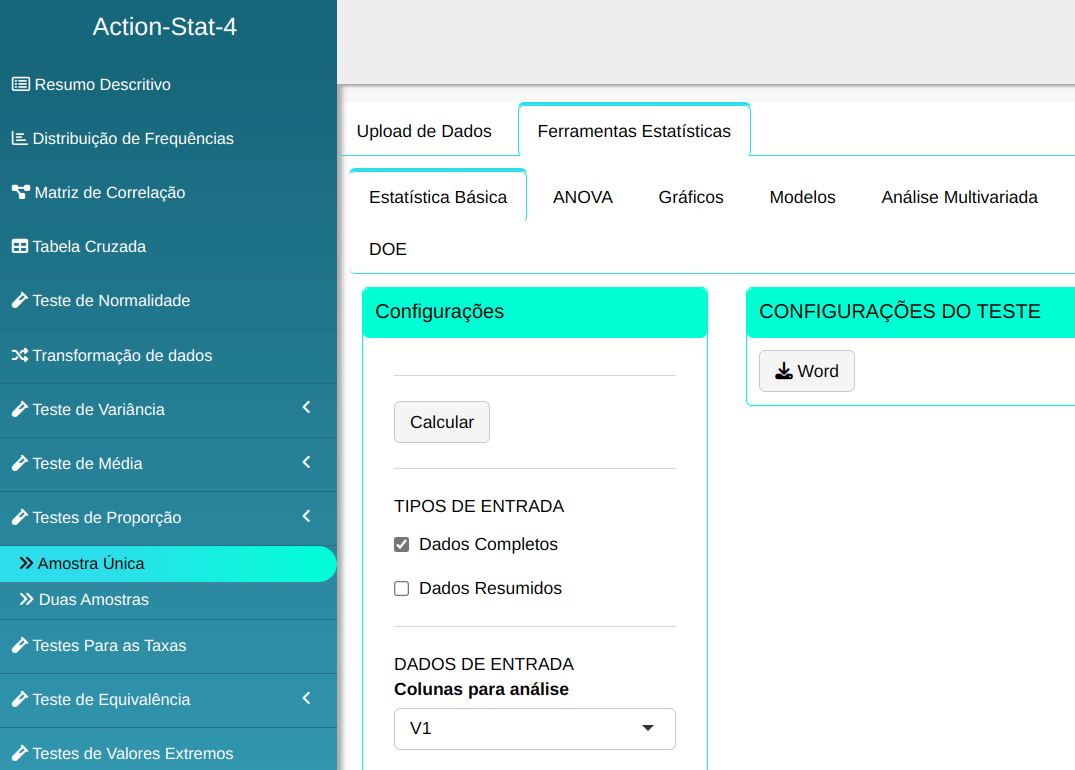
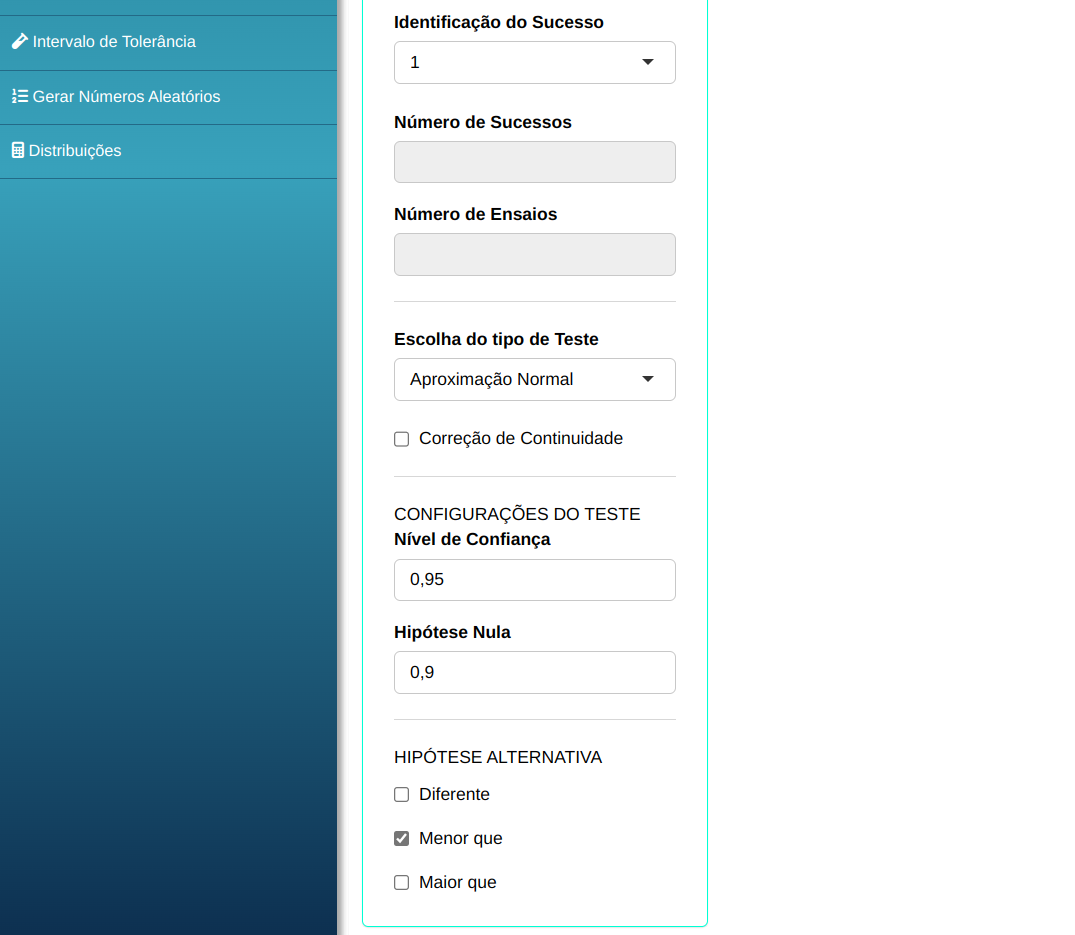
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Resultados
| Quantidade | Proporções | |
|---|---|---|
| Sucesso | 175 | 0.875 |
| Fracasso | 25 | 0.125 |
Resultados
| Valores | |
|---|---|
| Estatística Z | -1.178511 |
| P-valor | 0.1192964 |
| Proporção de sucesso na amostra | 0.875 |
| Hipótese Alternativa Menor que | 0.9 |
| Nível de Confiança | 95% |
| Limite Inferior | 0 |
| Limite Superior | 0.9134655 |
A estatística do teste é -1,178511. Como o P-valor é 0,1192964 > 0,05 então, a um nível de significância de 5%, temos evidências de que a proporção é igual a 0,9.
Exemplo 2:
Um fabricante garante que 90% das peças que fornece à linha de produção de uma determinada fábrica concorda com as especificações exigidas. A análise de uma amostra de 200 peças revelou 25 defeituosas. A um nível de 5%, podemos dizer que é verdadeira a afirmação do fabricante?
Faremos o teste de proporção.
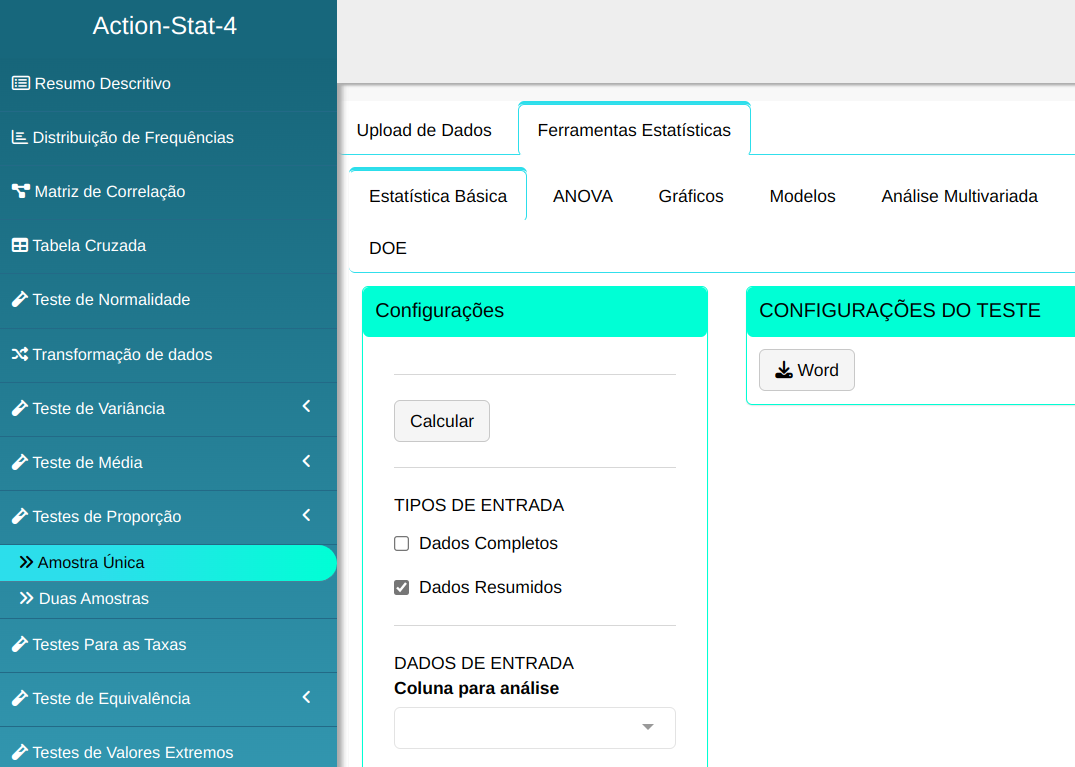
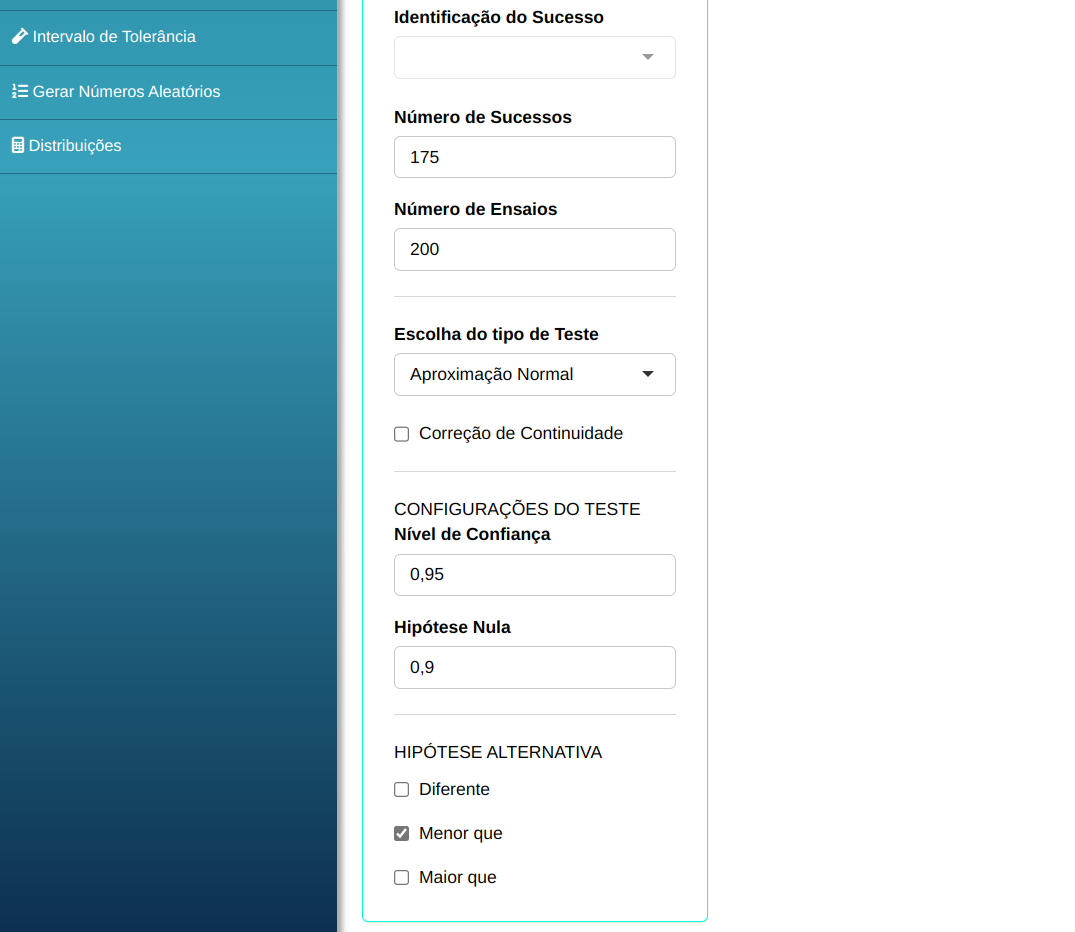
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Resultados
| Quantidade | Proporções | |
|---|---|---|
| Sucesso | 175 | 0.875 |
| Fracasso | 25 | 0.125 |
Resultados
| Valores | |
|---|---|
| Estatística Z | -1.178511 |
| P-valor | 0.1192964 |
| Proporção de sucesso na amostra | 0.875 |
| Hipótese Alternativa Menor que | 0.9 |
| Nível de Confiança | 95% |
| Limite Inferior | 0 |
| Limite Superior | 0.9134655 |
A estatística do teste é -1,178511. Como o P-valor é 0,1192964 > 0,05 então, a um nível de significância de 5%, temos evidências de que a proporção é igual a 0,9.