2. Proporções: Duas amostras
O teste de proporções para duas amostras é usado para comparar a taxa de sucesso dos experimentos.
Exemplo 1:
Uma empresa que presta serviços de assessoria econômica a outras empresas está interessada em comparar a taxa de reclamações sobre os seus serviços em dois de seus escritórios em duas cidades diferentes. Suponha que a empresa tenha selecionado aleatoriamente 100 serviços realizados pelo escritório da cidade A e 120 serviços realizados pelo escritório da cidade B. As tabelas mostram esses serviços (1 indica que não houve reclamação e 0 indica que houve reclamação). A empresa deseja saber se estes resultados são suficientes para se concluir que os dois escritórios apresentam diferença significativa entre suas taxas de reclamações.
| Grupo | Valor |
|---|---|
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 1 |
| Amostra 1 | 0 |
| Amostra 1 | 0 |
| Amostra 1 | 0 |
| Amostra 1 | 0 |
| Amostra 1 | 0 |
| Amostra 1 | 0 |
| Amostra 1 | 0 |
| Amostra 1 | 0 |
| Amostra 1 | 0 |
| Amostra 1 | 0 |
| Amostra 1 | 0 |
| Amostra 1 | 0 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 1 |
| Amostra 2 | 0 |
| Amostra 2 | 0 |
| Amostra 2 | 0 |
| Amostra 2 | 0 |
| Amostra 2 | 0 |
| Amostra 2 | 0 |
| Amostra 2 | 0 |
| Amostra 2 | 0 |
| Amostra 2 | 0 |
| Amostra 2 | 0 |
| Amostra 2 | 0 |
| Amostra 2 | 0 |
| Amostra 2 | 0 |
| Amostra 2 | 0 |
| Amostra 2 | 0 |
| Amostra 2 | 0 |
| Amostra 2 | 0 |
| Amostra 2 | 0 |
Faremos o Upload dos dados no sistema.
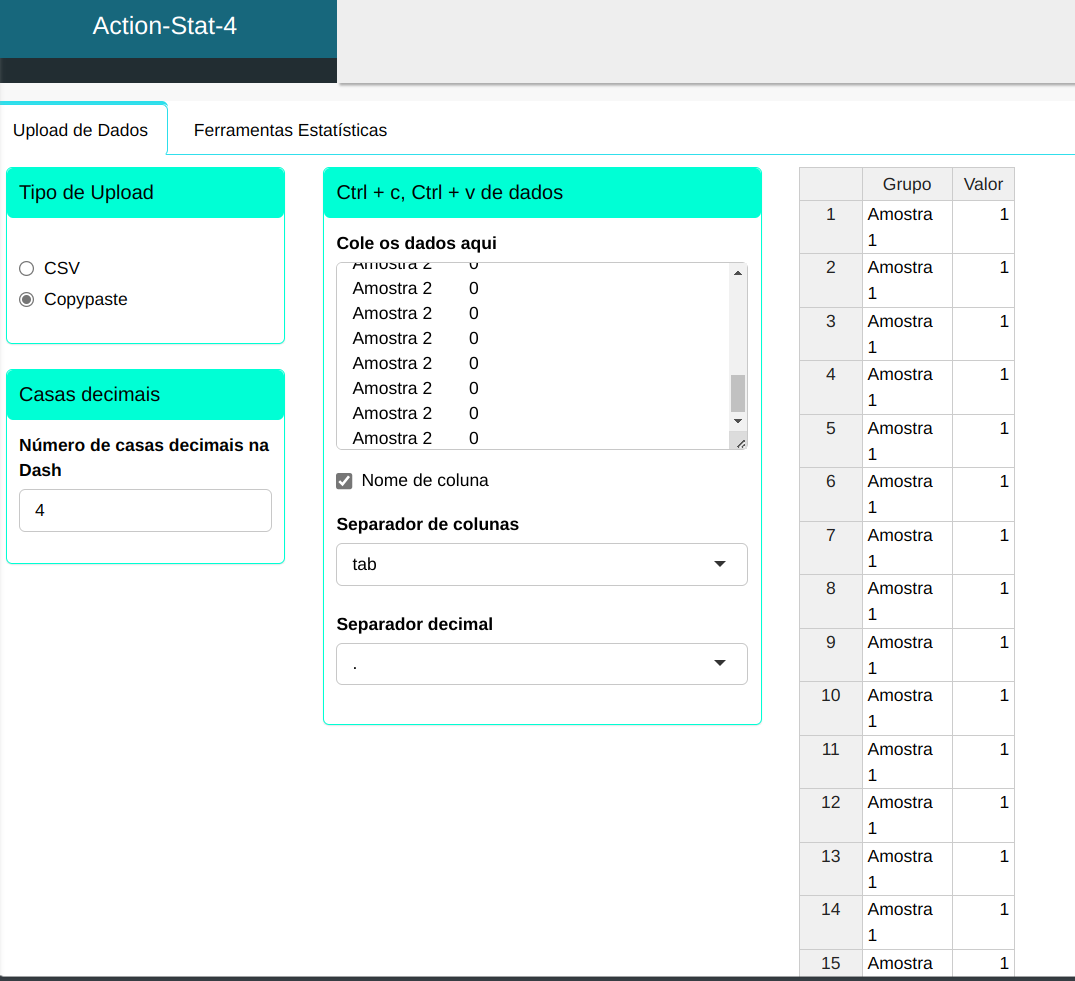
Para realizar um teste de proporções, a seguinte configuração é realizada, conforme mostrado na figura a seguir.
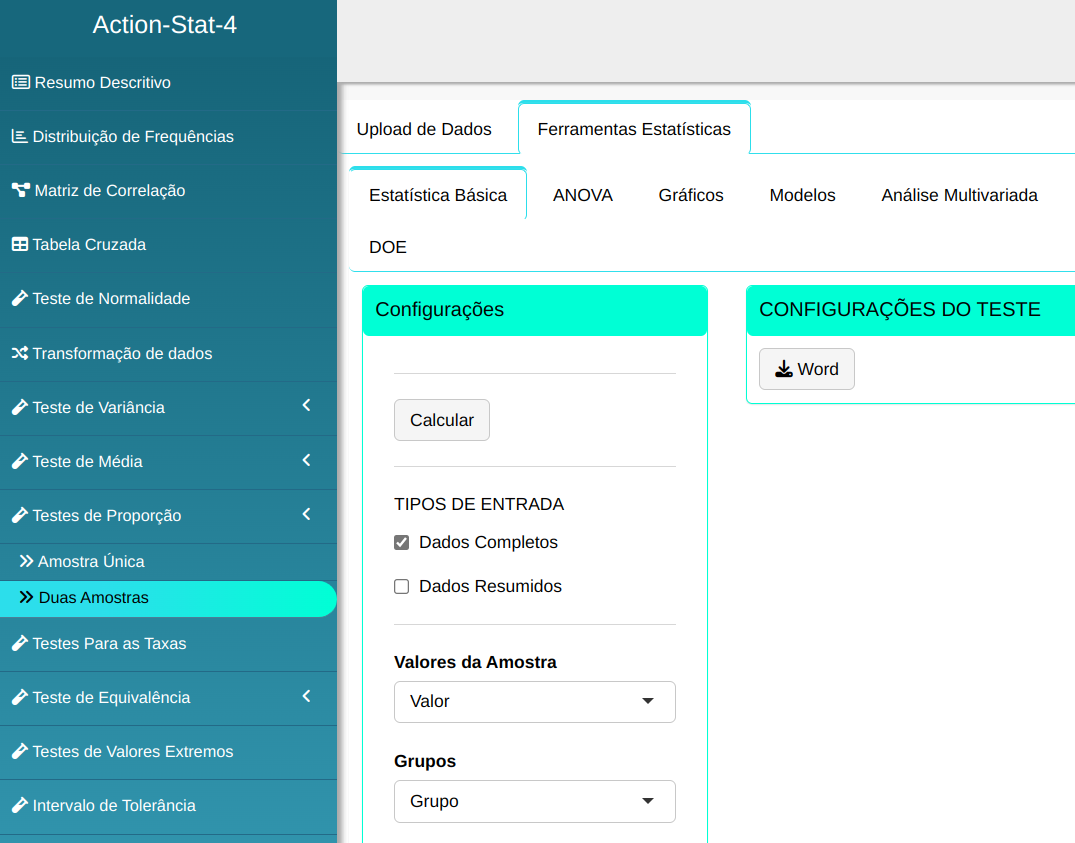
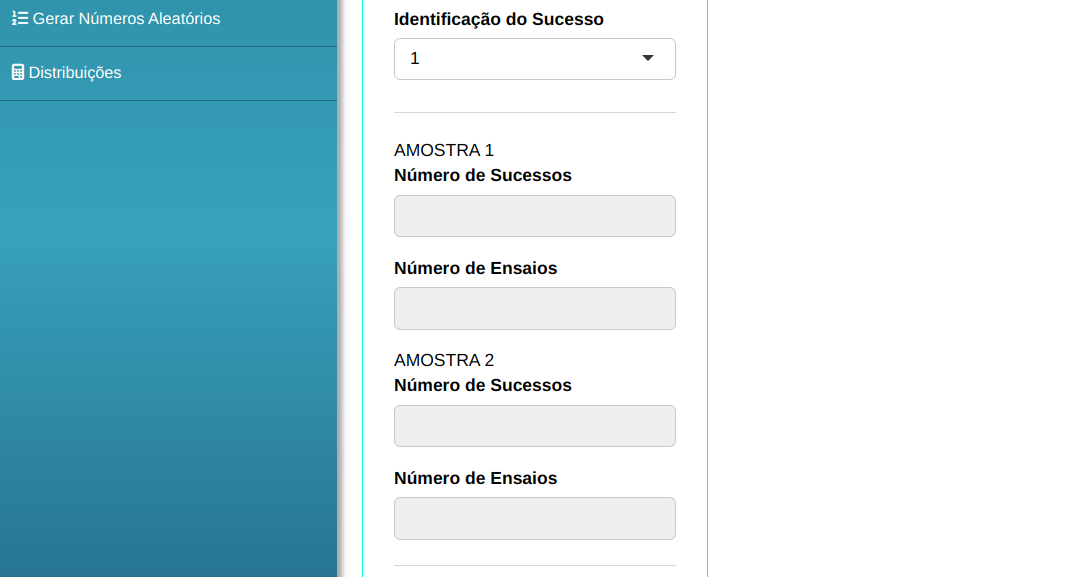
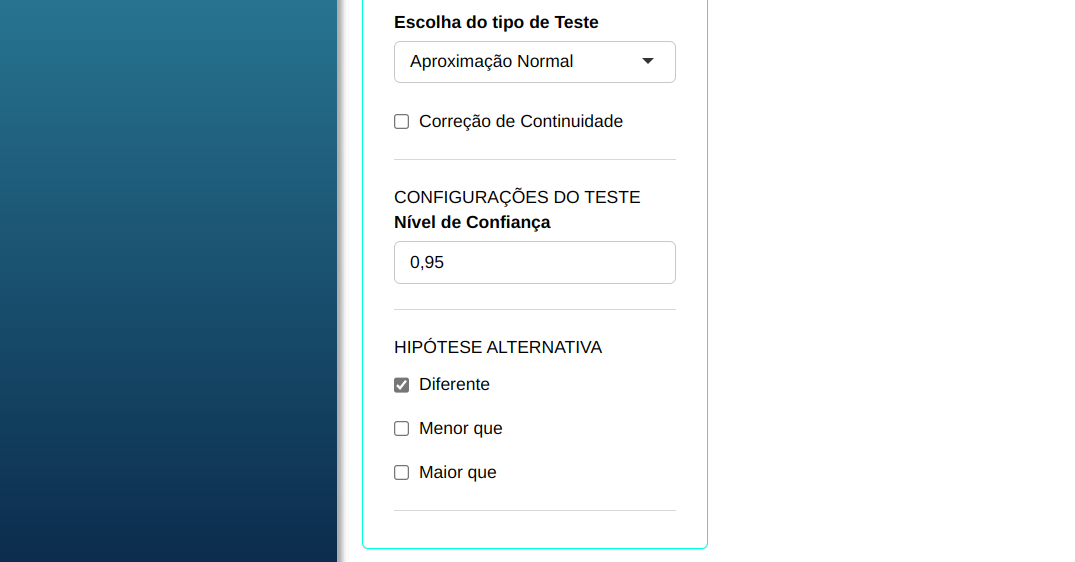
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Resultados - Amostra 1
| Quantidade | Proporções | |
|---|---|---|
| Sucesso | 88 | 0.88 |
| Fracasso | 12 | 0.12 |
Resultados - Amostra 2
| Quantidade | Proporções | |
|---|---|---|
| Sucesso | 102 | 0.85 |
| Fracasso | 18 | 0.15 |
Resultados - Aproximação Normal
| Valores | |
|---|---|
| Estatística Z | 0.6456331 |
| P-valor | 0.518517 |
| Proporção de Sucesso em Amostra 1 | 0.88 |
| Proporção de Sucesso em Amostra 2 | 0.85 |
| Hipótese Alternativa | Diferente de 0 |
| Nível de Confiança | 95% |
| Limite Inferior | -0.06021159 |
| Limite Superior | 0.1202116 |
Como o p-valor obtido, 0,518517, é maior que o nível de significância adotado, de 0,05, portanto não rejeitamos a hipótese nula, de igualdade entre as proporções. Assim, não há evidências para dizermos que os escritórios apresentam diferença significativa entre suas taxas de reclamações.
Exemplo 2:
Uma empresa que presta serviços de assessoria econômica a outras empresas estão interessadas em comparar a taxa de reclamações sobre os seus serviços em dois de seus escritórios em duas cidades diferentes. Suponha que a empresa tenha selecionado aleatoriamente 100 serviços realizados pelo escritório da cidade A e foi constatado que em 12 deles houve algum tipo de reclamação. Já do escritório da cidade B foram selecionados 120 serviços e 18 receberam algum tipo de reclamação. A empresa deseja saber se estes resultados são suficientes para se concluir que os dois escritórios apresentam diferença significativa entre suas taxas de reclamações.
Para realizar um teste de proporções, a seguinte configuração é realizada, conforme mostrado na figura a seguir.
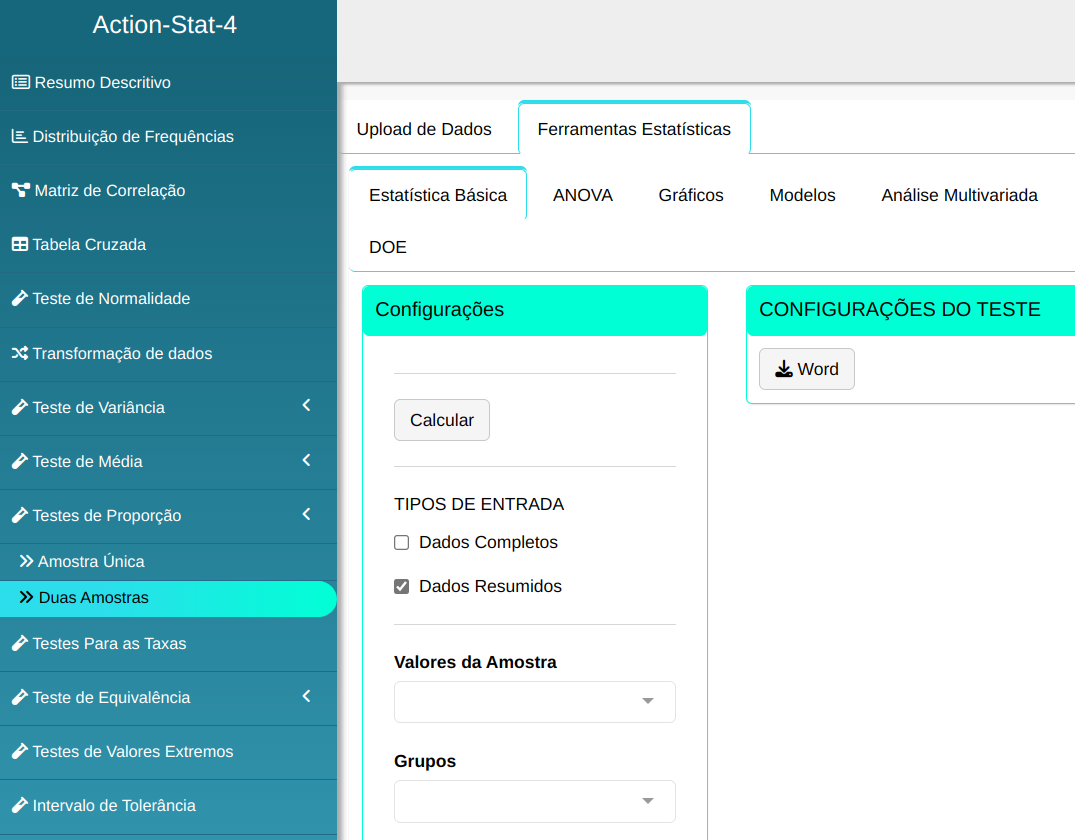
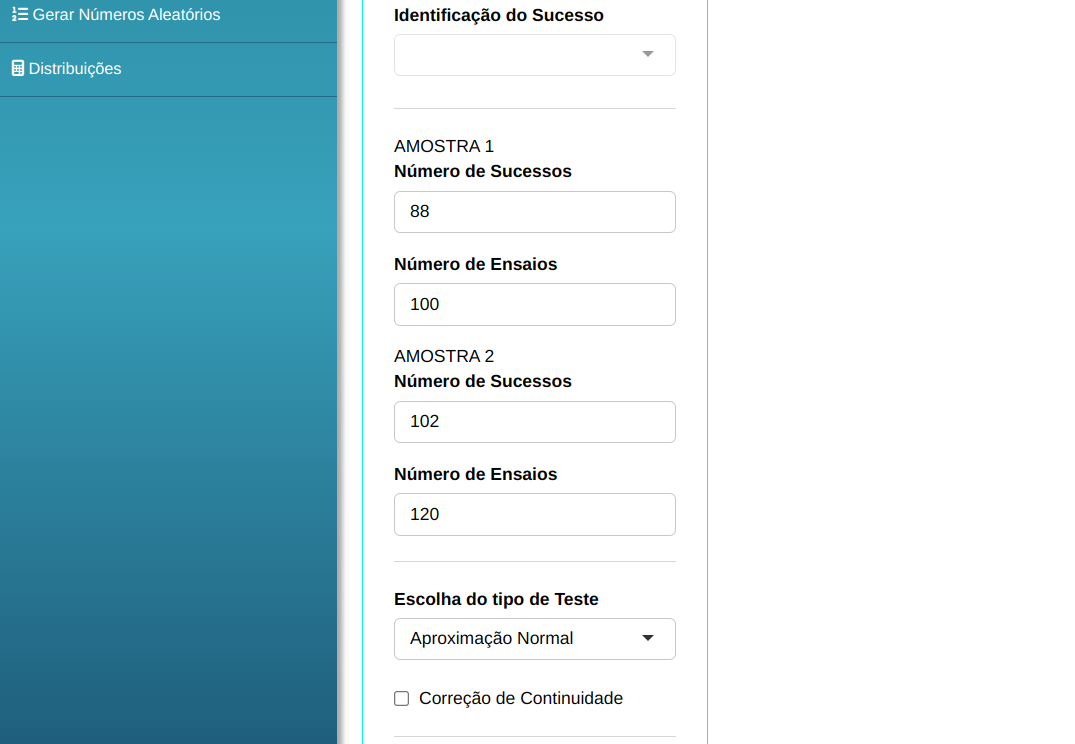
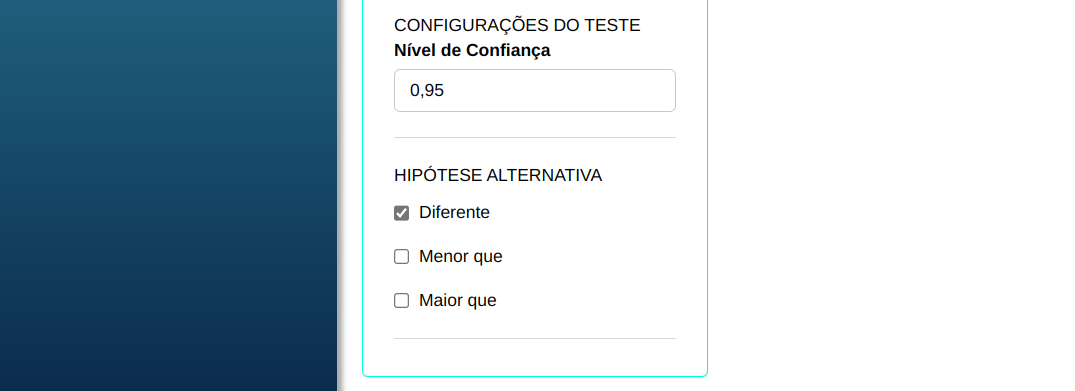
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Resultados - Conjunto de Dados 1
| Quantidade | Proporções | |
|---|---|---|
| Sucesso | 88 | 0.88 |
| Fracasso | 12 | 0.12 |
Resultados - Conjunto de Dados 2
| Quantidade | Proporções | |
|---|---|---|
| Sucesso | 102 | 0.85 |
| Fracasso | 18 | 0.15 |
Resultados - Aproximação Normal
| Valores | |
|---|---|
| Estatística Z | 0.6456331 |
| P-valor | 0.518517 |
| Proporção de Sucesso na Amostra 1 | 0.88 |
| Proporção de Sucesso na Amostra 2 | 0.85 |
| Hipótese Alternativa | Diferente de 0 |
| Nível de Confiança | 95% |
| Limite Inferior | -0.06021159 |
| Limite Superior | 0.1202116 |
Como o p-valor obtido, 0,518517, é maior que o nível de significância adotado, de 0,05, portanto não rejeitamos a hipótese nula, de igualdade entre as proporções. Assim, não há evidências para dizermos que os escritórios apresentam diferença significativa entre suas taxas de reclamações.