1. Teste de variância: uma variância
O teste Qui-quadrado é usado para analisar se a variância do conjunto de dados é diferente do valor esperado.
Detalhes:
O teste de uma variância assume que o conjunto de dados apresenta distribuição normal. A hipótese nula e a hipótese alternativa são definidas em termos da variância populacional (ou do desvio padrão populacional).
Exemplo 1:
O peso de componentes mecânicos produzidos por uma determinada empresa é uma variável aleatória que se supõe ter distribuição Normal. Para análisar a variabilidade desse peso, foi coletada uma amostra de 11 componentes.
| 98 |
| 97 |
| 102 |
| 100 |
| 98 |
| 101 |
| 102 |
| 105 |
| 95 |
| 102 |
| 100 |
Faremos então o upload dos dados.
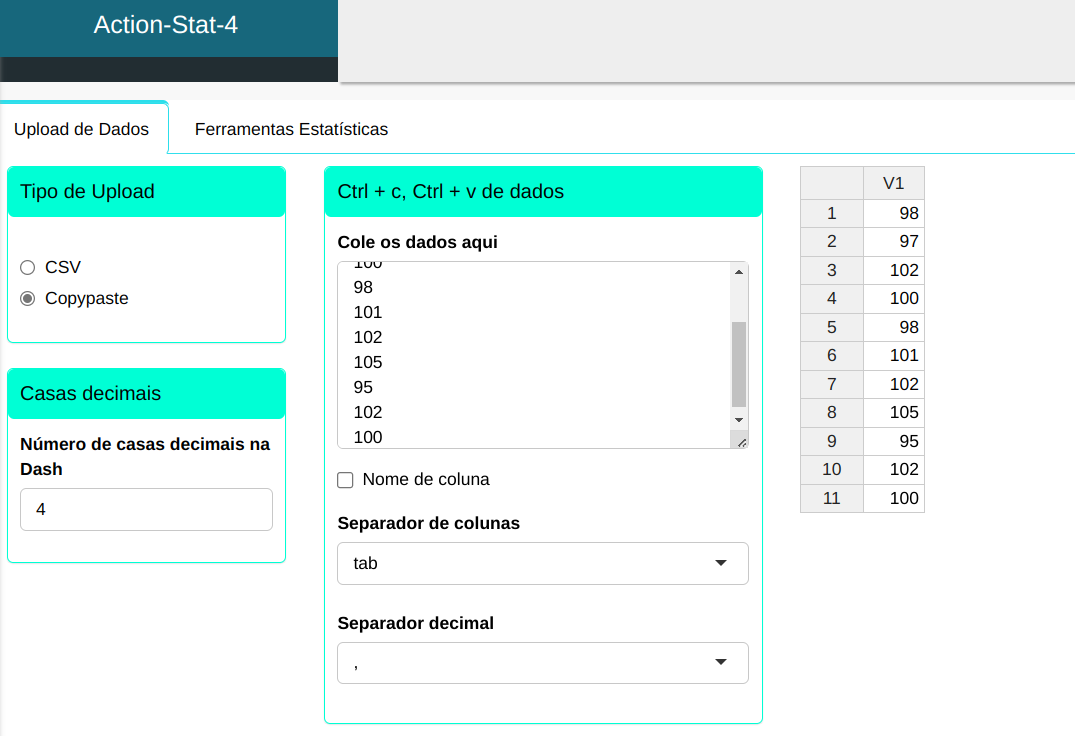
Para realizar um teste de variância, é preparado de acordo com a configuração mostrada na figura abaixo.
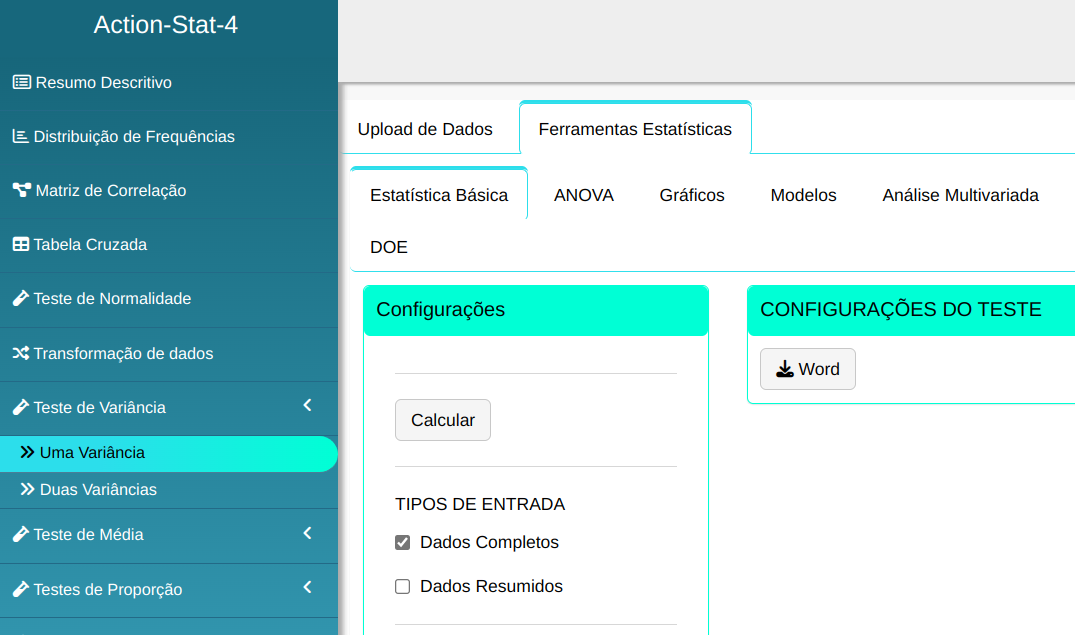
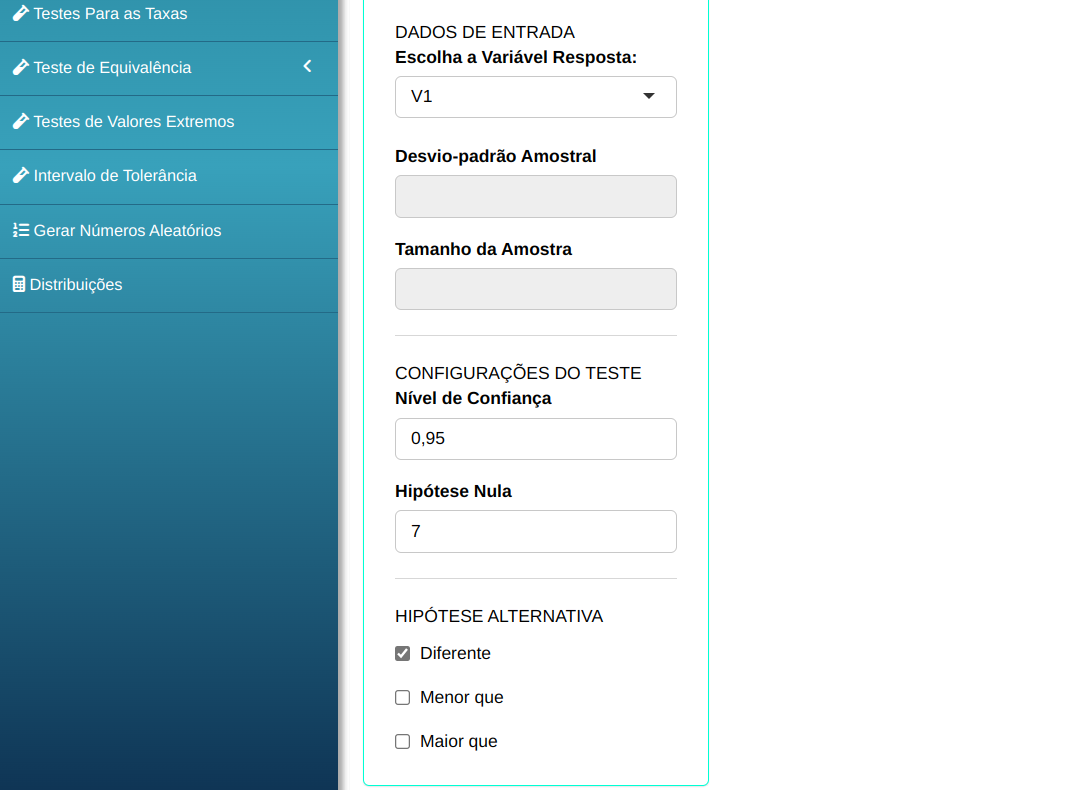
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Teste para Uma Variância
| Valor | |
|---|---|
| Graus de Liberdade | 10 |
| Estatística Qui-Quadrado | 11.4285 |
| P-valor | 0.6502338 |
| Variancia Amostral | 8 |
| Tamanho da Amostra | 11 |
| Hipótese Alternativa: Diferente | 7 |
| Nível de Confiança | 95% |
| Limite Inferior | 3.905644 |
| Limite Superior | 24.63833 |
Como o p-valor é 0,65 > 0,05 então, ao nível de significância de 5%, não rejeitamos a hipótese nula de que a variância dos dados é igual a 7. O intervalo de confiança de 95% para a variância é dado por IC = (3,9056;24,6383).
Exemplo 2:
Uma máquina de preenchimento automático é utilizada para encher garrafas com detergente líquido. Em uma amostra aleatória de 20 garrafas, a variância da amostra do volume de enchimento foi de $s^2$ = 0,0153 $(\text{onça fluida})^2$. Se a variância do volume de enchimento exceder 0,01 $(\text{onça fluida})^2$, existirá uma proporção inaceitável de garrafas cujo enchimento não foi completo ou foi em demasia. Há evidência nos dados da amostra sugerindo que o fabricante tenha um problema com garrafas na falta ou no excesso de detergente? Utilize $ \alpha$ = 0,05, assumindo que o volume de enchimentos segue uma distribuição normal. Considere também que está sendo realizado um teste de hipóteses para a variância com hipótese nula $H_0 : \sigma^2$ = 0,01.
Para realizar o teste de variância ele é preparado conforme a configuração mostrada na figura abaixo.
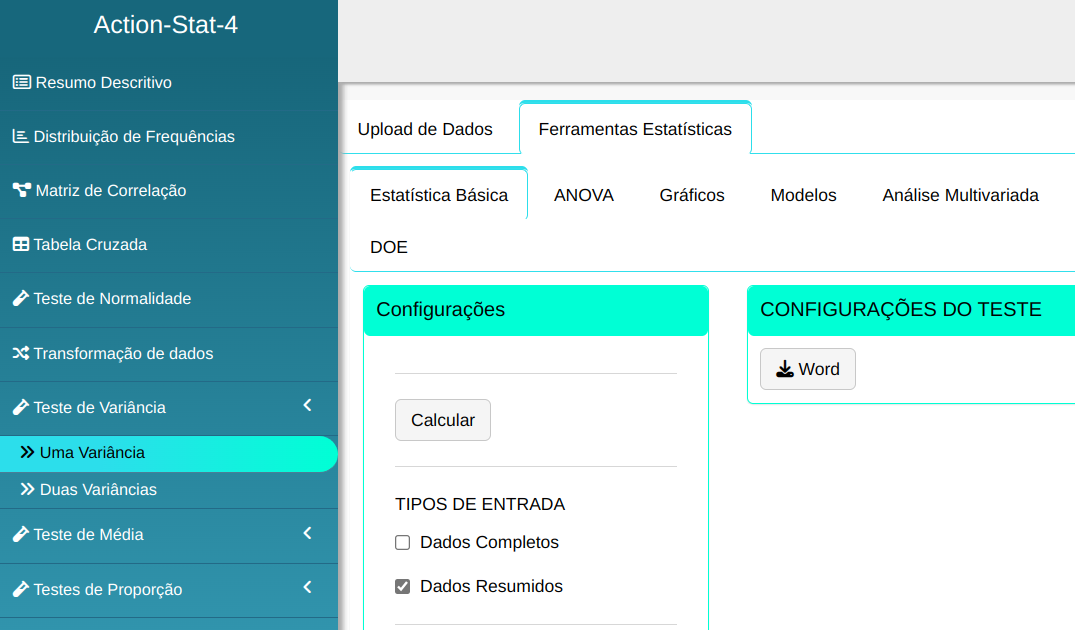
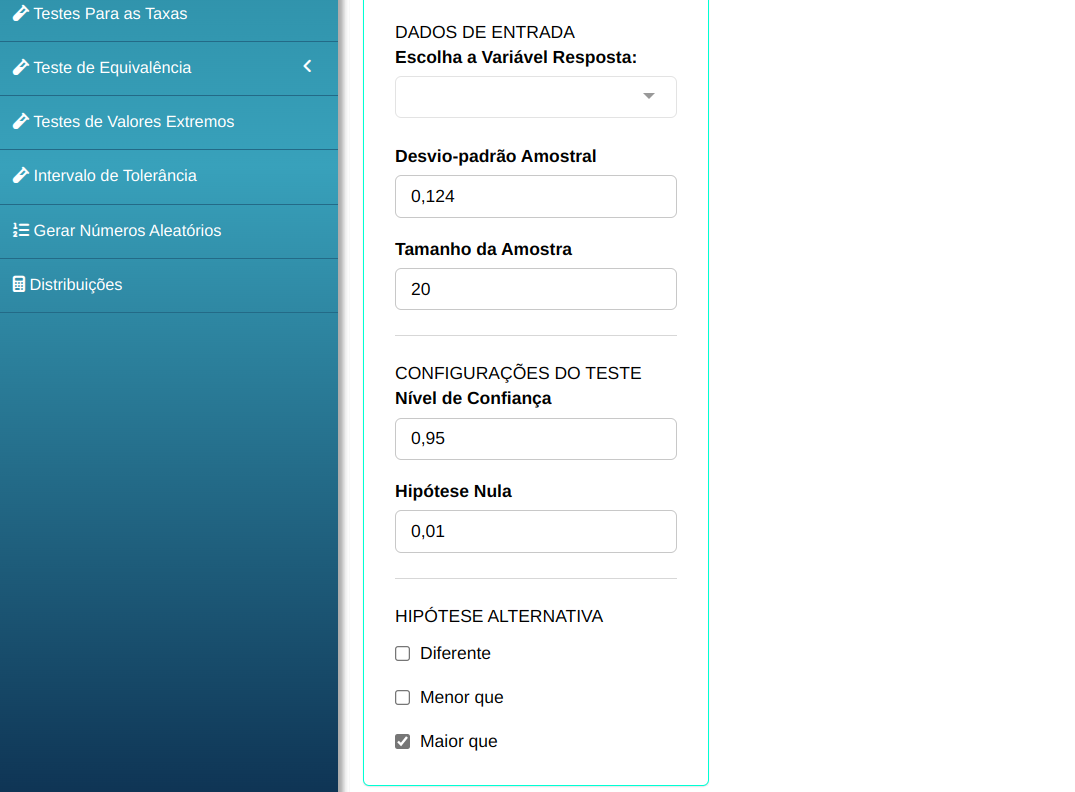
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Teste para Uma Variância
| Valor | |
|---|---|
| Graus de Liberdade | 19 |
| Estatística Qui-Quadrado | 29.2144 |
| P-valor | 0.06268668 |
| Variância Amostral | 0.015376 |
| Tamanho da Amostra | 20 |
| Hipótese Alternativa: Maior que | 0.01 |
| Nível de Confiança | 95% |
| Limite Inferior | 0.009691766 |
| Limite Superior | inf |
Como o p-valor é igual a 0,06268668 > 0,05 = 5%, não rejeitamos a hipótese nula. Ou seja, temos evidências de que a variância não excede o valor de 0,01.