2. Teste de variância: Duas Variâncias
O teste F é utilizado para analisar a variância entre dois conjuntos de dados diferentes e compará-los utilizando o teste de hipóteses.
Exemplo 1:
Um analista da qualidade quer avaliar se existe diferença nas medidas de eixos comandos desenvolvidos por dois sistemas de usinagem. A Tabela a seguir apresenta as medições de duas populações dos dois sistemas que são independentes e tem distribuição normal. A um nível de 95% de confiança, existe diferença significativa entre as variabilidades das medidas dos eixos comandos dos dois sistemas de usinagem?
| Sistema de Usinagem | Eixo de Comando |
|---|---|
| Sistema 1 | 18,7997 |
| Sistema 1 | 20,5035 |
| Sistema 1 | 18,6214 |
| Sistema 1 | 19,9192 |
| Sistema 1 | 21,117 |
| Sistema 1 | 18,7545 |
| Sistema 1 | 19,2026 |
| Sistema 1 | 18,4187 |
| Sistema 1 | 20,7641 |
| Sistema 1 | 21,0553 |
| Sistema 1 | 19,1688 |
| Sistema 1 | 19,2898 |
| Sistema 1 | 22,059 |
| Sistema 1 | 18,5854 |
| Sistema 1 | 17,8896 |
| Sistema 1 | 20,8353 |
| Sistema 1 | 17,527 |
| Sistema 1 | 17,078 |
| Sistema 1 | 17,6197 |
| Sistema 1 | 21,4255 |
| Sistema 1 | 17,5905 |
| Sistema 1 | 18,7561 |
| Sistema 1 | 18,9772 |
| Sistema 1 | 20,3084 |
| Sistema 1 | 18,8988 |
| Sistema 2 | 21,1609 |
| Sistema 2 | 26,1371 |
| Sistema 2 | 21,4737 |
| Sistema 2 | 30,9934 |
| Sistema 2 | 22,8421 |
| Sistema 2 | 24,4133 |
| Sistema 2 | 20,4137 |
| Sistema 2 | 25,5475 |
| Sistema 2 | 21,8791 |
| Sistema 2 | 22,6706 |
| Sistema 2 | 24,7531 |
| Sistema 2 | 25,7219 |
| Sistema 2 | 22,6389 |
| Sistema 2 | 26,2308 |
| Sistema 2 | 26,7998 |
| Sistema 2 | 28,4708 |
| Sistema 2 | 26,9941 |
| Sistema 2 | 25,1489 |
| Sistema 2 | 24,6179 |
| Sistema 2 | 27,0194 |
| Sistema 2 | 25,0589 |
| Sistema 2 | 22,1119 |
| Sistema 2 | 20,3069 |
| Sistema 2 | 23,6758 |
| Sistema 2 | 27,1201 |
| Sistema 2 | 29,6136 |
| Sistema 2 | 25,9948 |
| Sistema 2 | 18,223 |
| Sistema 2 | 23,7336 |
| Sistema 2 | 22,4208 |
Faremos então o upload dos dados no sistema.
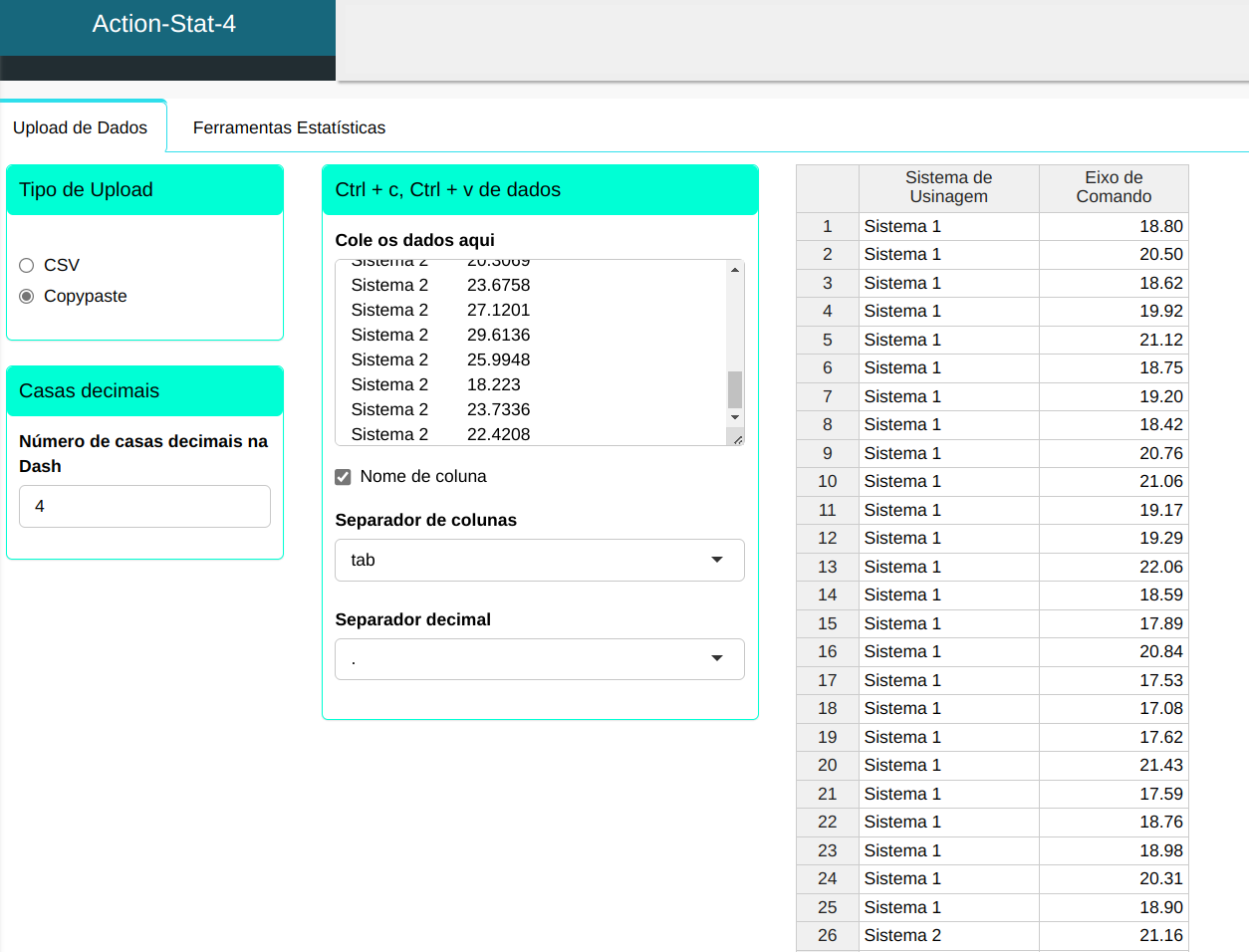
Para realizar um teste de duas variância, é elaborado de acordo com a configuração mostrada na figura abaixo.
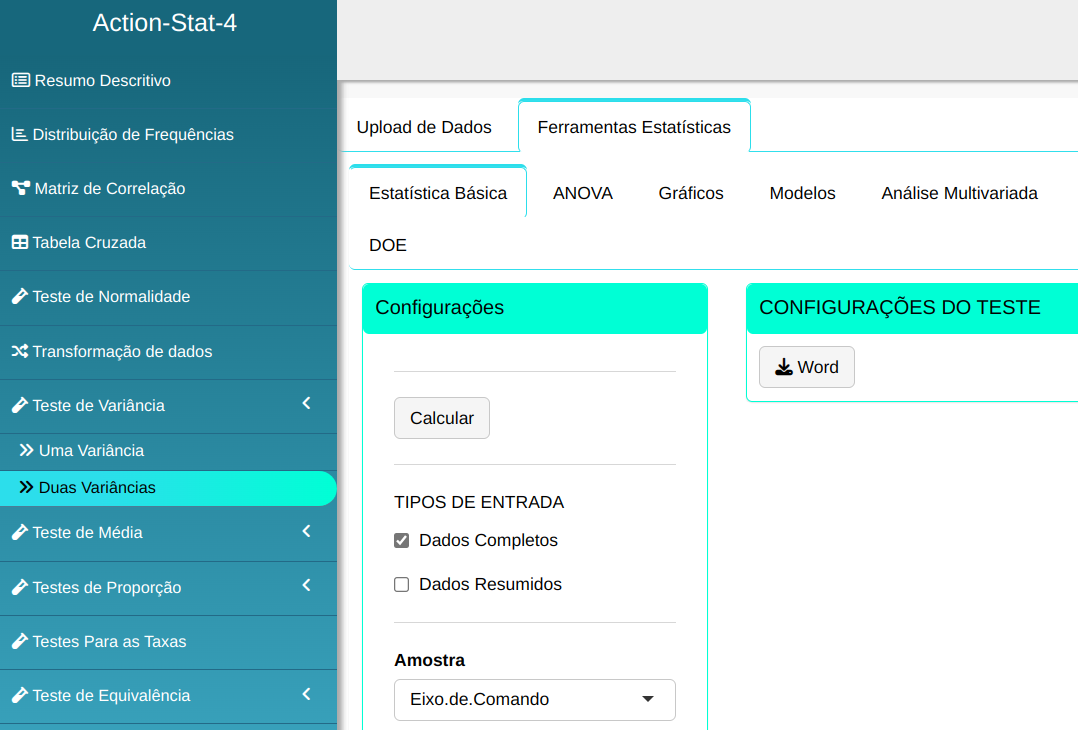
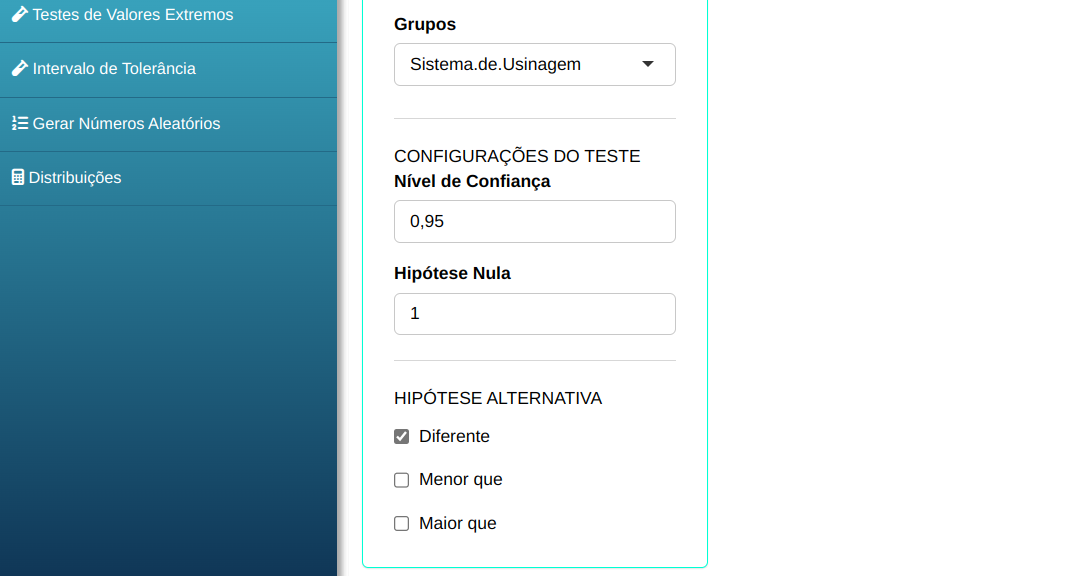
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados foram:
Teste para Duas Variâncias
| Valores | |
|---|---|
| Estatística F | 0.222586 |
| Graus de liberdade (Numerador) | 24 |
| Graus de liberdade (Denominador) | 29 |
| P-Valor | 0.0003578537 |
| Desvio padrão - Sistema 1 | 1.362343 |
| Desvio padrão - Sistema 2 | 2.887603 |
| Tamanho de Sistema 1 | 25 |
| Tamanho de Sistema 2 | 30 |
| Hipótese Alternativa Diferente de | 1 |
| Intervalo de Confiança para razão das Variâncias | 95% |
| Limite inferior | 0.1033358 |
| Limite Superior | 0.4935717 |
Intervalo de Confiança para Desvio padrão
| Limite Inferior | Desvio Padrão | Limite Superior | |
|---|---|---|---|
| Sistema 1 | 1.064 | 1.362 | 1.895 |
| Sistema 2 | 2.300 | 2.888 | 3.882 |
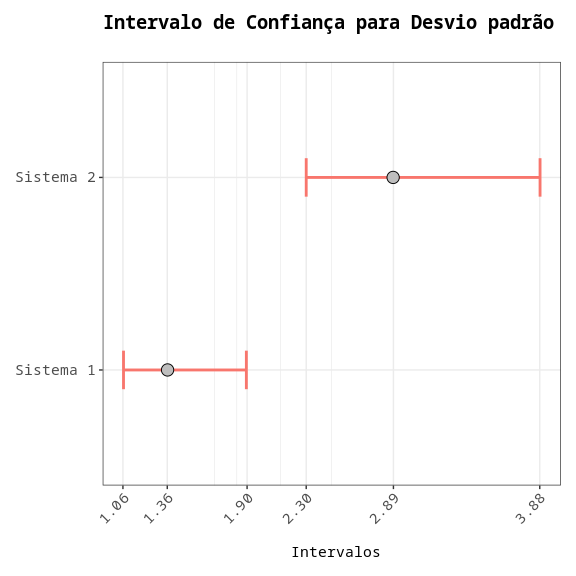
Fazendo o teste F para duas variâncias, vemos que o p-valor é 0,0003578, ou seja, menor que 5%. Assim, rejeitamos a hipótese de que as variâncias são iguais.
Exemplo 2:
Um analista da qualidade quer avaliar se existe diferença nas medidas de eixos comandos desenvolvidos por dois sistemas de usinagem. Os valores dos desvios padrão são 1,362346 e 2,887603 e os tamanhos de amostra são 25 e 20. A um nível de 95% de confiança, existe diferença significativa entre as variabilidades das medidas dos eixos comandos dos dois sistemas de usinagem?
Para realizar um teste de duas variância, a seguinte configuração é realizada, conforme mostrado na figura a seguir.
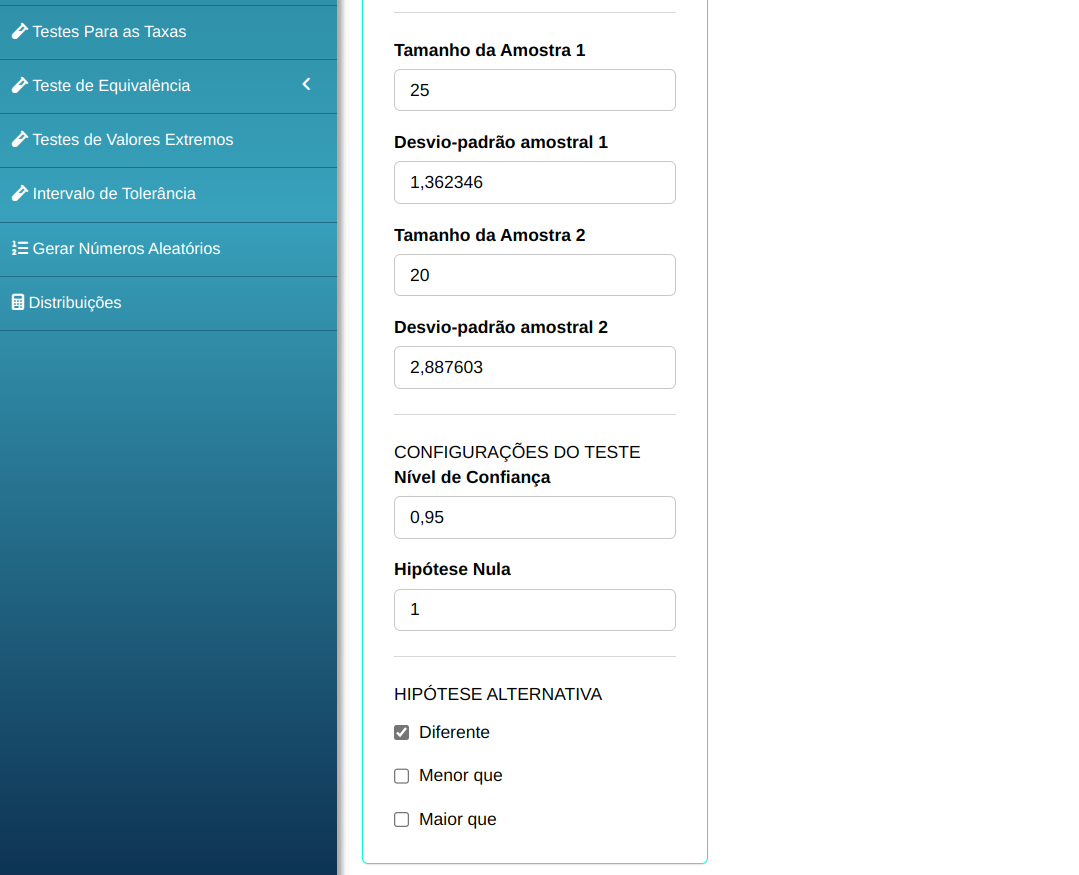
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados foram:
Teste para Duas Variâncias
| Valores | |
|---|---|
| Estatística F | 0.222587 |
| Graus de liberdade (Numerador) | 24 |
| Graus de liberdade (Denominador) | 19 |
| P-Valor | 0.000716142 |
| Desvio padrão - Amostra 1 | 1.362346 |
| Desvio padrão - Amostra 2 | 2.887603 |
| Tamanho da Amostra 1 | 25 |
| Tamanho da Amostra 2 | 20 |
| Hipóte Alternativa Diferente de | 1 |
| Intervalo de Confiança para razão das Variâncias | 95% |
| Limite Inferior | 0.09076587 |
| Limite Superior | 0.5220008 |
Intervalo de Confiança para Desvio padrão
| Limite Inferior | Desvio Padrão | Limite Superior | |
|---|---|---|---|
| Amostra 1 | 1.0638 | 1.3623 | 1.8952 |
| Amostra 2 | 2.196 | 2.8876 | 4.2176 |
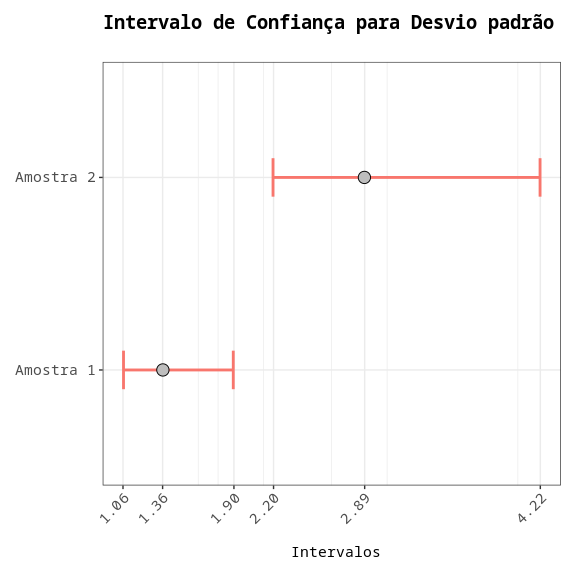
Fazendo o teste F para duas variâncias, vemos que o p-valor é 0,0003578, ou seja, menor que 5%. Assim, rejeitamos a hipótese de que as variâncias são iguais.