1. Análise de Processos (CEP)
A orientação da ANVISA exige que as diversas indústrias farmacêuticas realizem uma avaliação estatística dos resultados do controle do produto em processo e do produto acabado. A metodologia aqui apresentada é bem fundamentada e segue os requisitos do Guia da ANVISA (2012). O Action Stat fornece uma ferramenta estatística que permite a geração de relatórios completos de análise da qualidade do produto, contendo uma metodologia estatística que segue o seguinte fluxo: primeiramente, é feita uma análise exploratória dos resultados com um resumo descritivo e um gráfico BoxPlot. Em seguida, é realizado um teste de ajuste da distribuição. Depois, é avaliada a estabilidade do processo por meio de cartas de controle. Segue-se uma avaliação da capacidade e do desempenho do processo e, por fim, um teste de comparação de lotes múltiplos.
Para avaliar a estabilidade dos resultados ao longo do tempo, a análise por meio de gráficos de controle estatísticos de processo CEP é comumente utilizada. No entanto, essa técnica é recomendada apenas em casos em que não há muitos subgrupos de dados. A recomendação é de no máximo 150 subgrupos para garantir uma interpretação adequada do gráfico de controle. Em situações com mais de 150 subgrupos, a análise por séries temporais é mais adequada.
Exemplo 1:
Um analista mediu o teor de uma substância para 31 lotes de produção de um determinado comprimido ao longo do ano. O objetivo é gerar um relatório estatístico completo da revisão do processo:
| Lotes | Teor |
|---|---|
| 2400001 | 98,78 |
| 2400002 | 95,53 |
| 2400003 | 98,37 |
| 2400004 | 100,41 |
| 2400005 | 96,54 |
| 2400006 | 94,12 |
| 2400007 | 96,13 |
| 2400008 | 94,96 |
| 2400009 | 98,00 |
| 2400010 | 97,54 |
| 2400011 | 98,74 |
| 2400012 | 92,6 |
| 2400013 | 96,63 |
| 2400014 | 104,64 |
| 2400015 | 97,38 |
| 2400016 | 94,91 |
| 2400017 | 100,44 |
| 2400018 | 92,57 |
| 2400019 | 95,97 |
| 2400020 | 97,06 |
| 2400021 | 95,19 |
| 2400022 | 92,12 |
| 2400023 | 99,06 |
| 2400024 | 104,13 |
| 2400025 | 102,01 |
| 2400026 | 99,13 |
| 2400027 | 96,73 |
| 2400028 | 97,27 |
| 2400029 | 98,19 |
| 2400030 | 98,58 |
| 2400031 | 101,18 |
Faremos o upload dos dados no sistema.
Faremos a análise configurando conforme a figura abaixo.
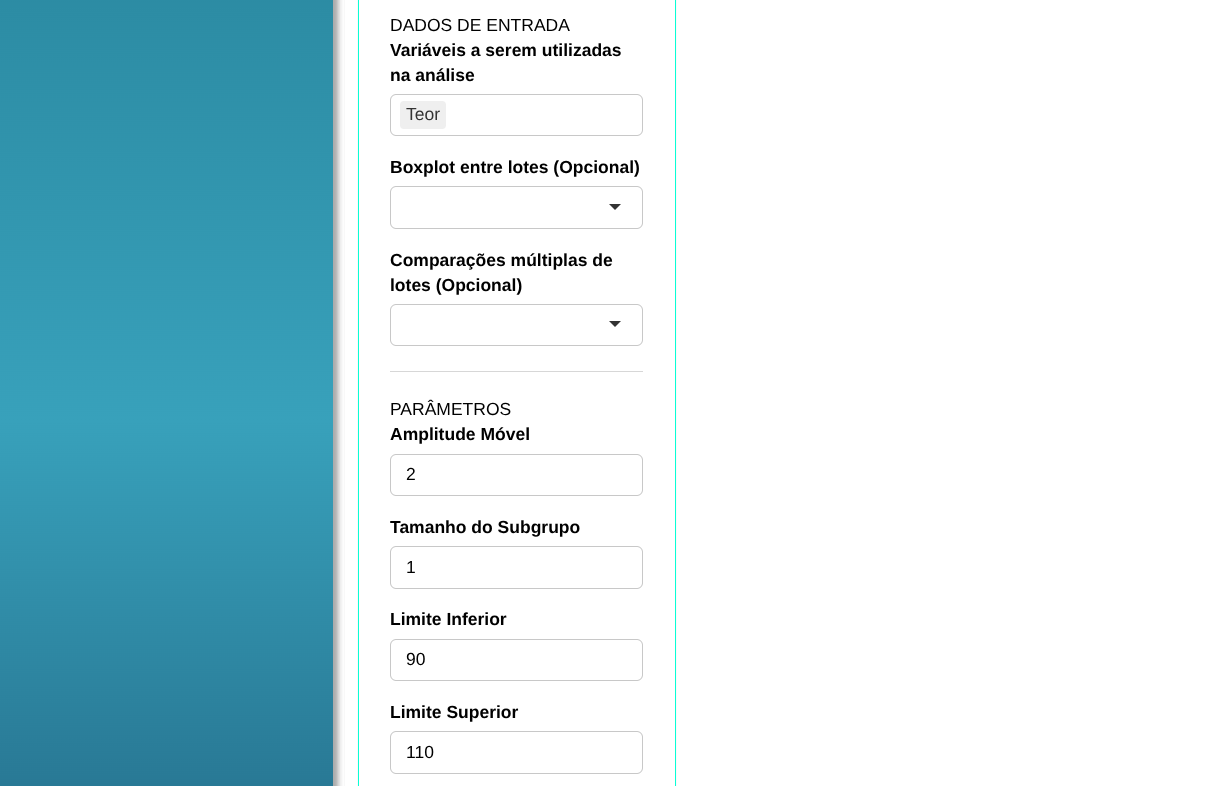
Em seguida, clique em Calcular para obter os resultados. Também pode gerar as análises e baixá-la em formato Word.
Os resultados são:
Resumo Descritivo
| Estatísticas | |
|---|---|
| Mínimo | 92.12 |
| 1º Quantil | 95.53 |
| Média | 97.5777 |
| Mediana | 97.38 |
| Tri-Média | 97.4736 |
| 3º Quantil | 99.06 |
| Máximo | 104.64 |
| Desvio Padrão | 3.0247 |
| Coeficiente de Variação (%) | 3.0998 |
| Assimetría | 0.3541 |
| Curtose | -0.1224 |
| Amplitude | 12.52 |
| Tamanho da Amostra | 31 |
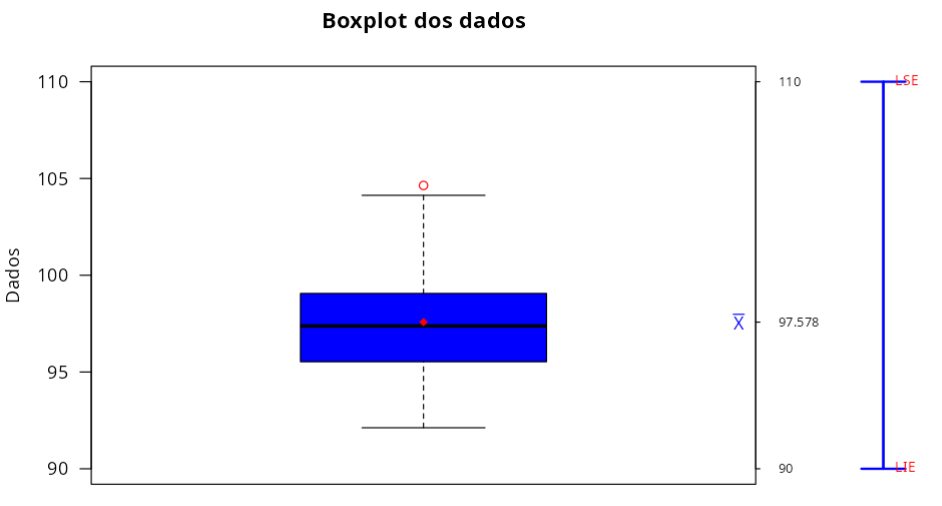
Outliers
| Ordem de Coleta | Dados | |
|---|---|---|
| 1 | 14 | 104.64 |
Análise Automática
| Análise do Processo | Situação | |
|---|---|---|
| 1 | Teste da Normalidad | Aceita ao nível de significância de 0.05 |
| 2 | Transformação de Box-Cox | Não Aplicável |
| 3 | Transformação de Johnson | Não Aplicável |
| 4 | Distribuição Não Normal | Não Aplicável |
| 5 | Distribuição Não Paramétrica | Não Aplicável |
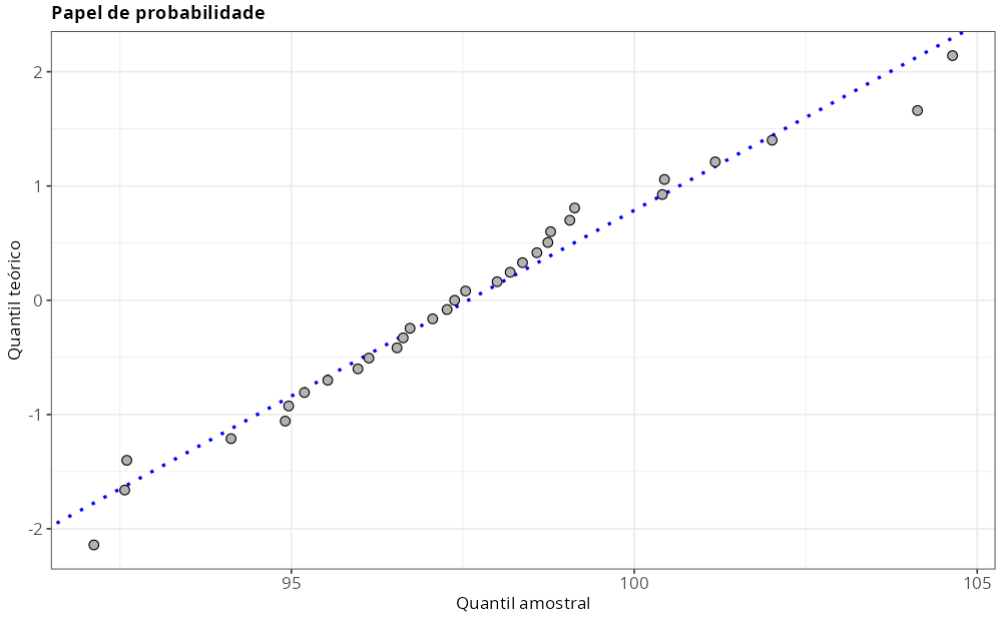
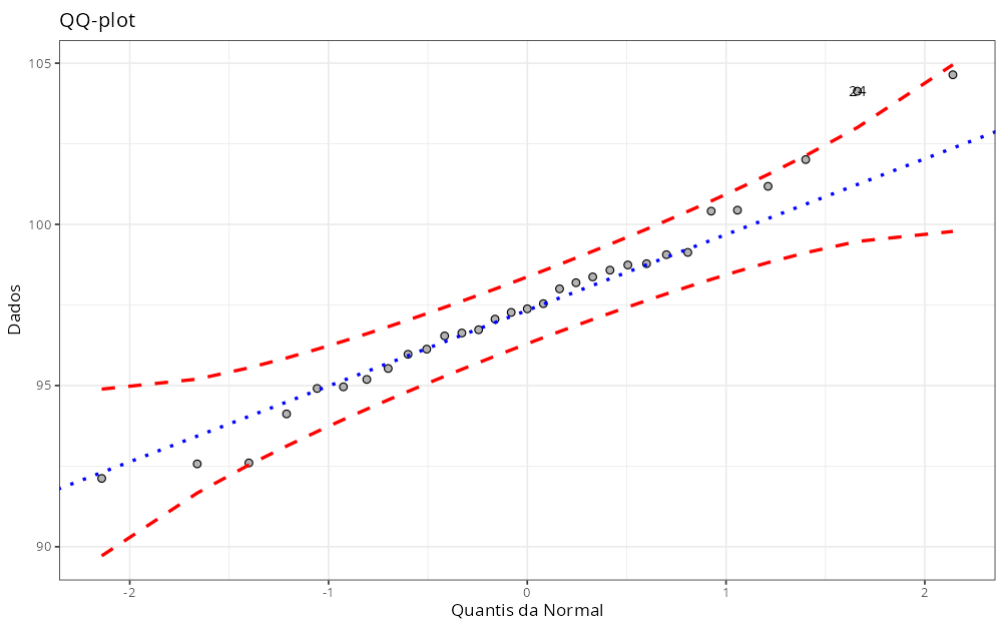
Teste da Normalidade
| Estatística | P-valor | |
|---|---|---|
| Anderson Darling | 0.2613 | 0.6836 |
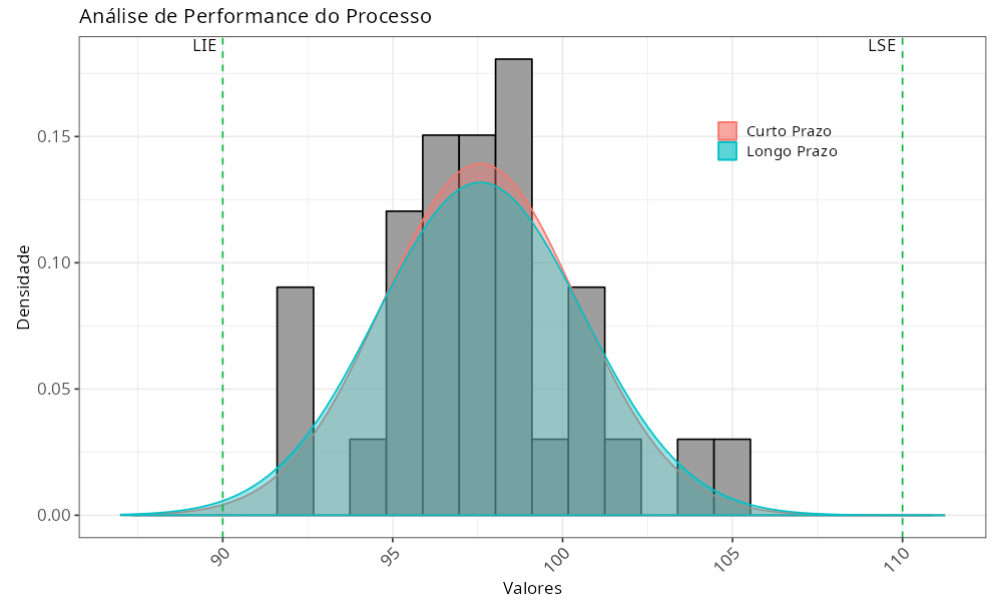
Especificações
| Valor | ||
|---|---|---|
| 1 | Amostra | 31 |
| 2 | Limite Inferior | 90 |
| 3 | Limite Superiior | 110 |
Estimativa
| Valor | |
|---|---|
| Média | 97.5777 |
| Desvio Padrão (Curto prazo) | 2.8625 |
| Desvio Padrão (Longo prazo) | 3.0247 |
Índice de Performance (Longo Prazo)
| Índices de Performance - Variabilidade Total | |
|---|---|
| PP | 1.1020 |
| PPI | 0.8351 |
| PPS | 1.3690 |
| PPK | 0.8351 |
Índices de Capacidade (Curto prazo)
| Índices de Capacidade (Variabilidade Inerente) | |
|---|---|
| CP | 1.1645 |
| CPL | 0.8824 |
| CPU | 1.4465 |
| CPK | 0.8824 |
Índices Observados
| Índices Observados | |
|---|---|
| PPM < LIE | 0 |
| PPM > LSE | 0 |
| PPM Total | 0 |
Índices Esperados (Longo Prazo)
| Índices Esperados (Variabilidade Total) | |
|---|---|
| PPM < LIE | 6118.1571 |
| PPM > LSE | 20.0514 |
| PPM Total | 6138.2086 |
Índices Esperados (Curto Prazo)
| Índices Esperados (Variabilidade Inerente) | |
|---|---|
| PPM < LIE | 4057.6342 |
| PPM > LSE | 7.1359 |
| PPM Total | 4064.7701 |
NÍVEL SIGMA
| Nível SIGMA | |
|---|---|
| Zbench (longo prazo) | 2.5041 |
| Zbench (curto prazo) | 2.6466 |
| Zshift | 1.5 |
| Metrica Sigma | 4.0041 |
Análise Gráfico
Estabilidade do Processo
Gráfico de Valores Individuais e Amplitudes Móveis
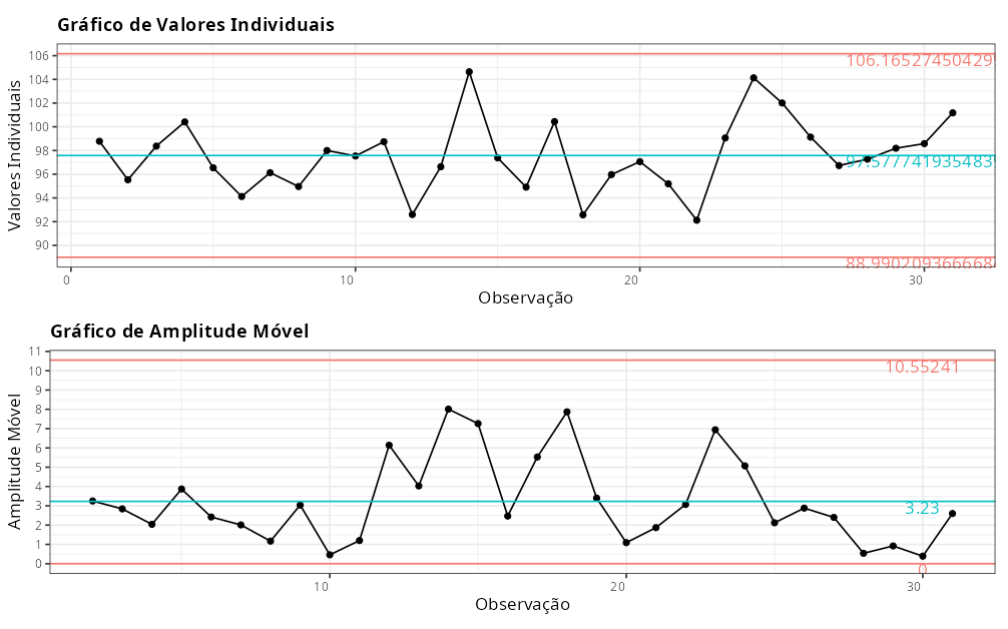
Gráfico de Valores Individuais
| Valor | |
|---|---|
| Limite Inferior de Controle | 88.9902 |
| Linha de Centro | 97.5777 |
| Limite Superior de Controle | 106.1653 |
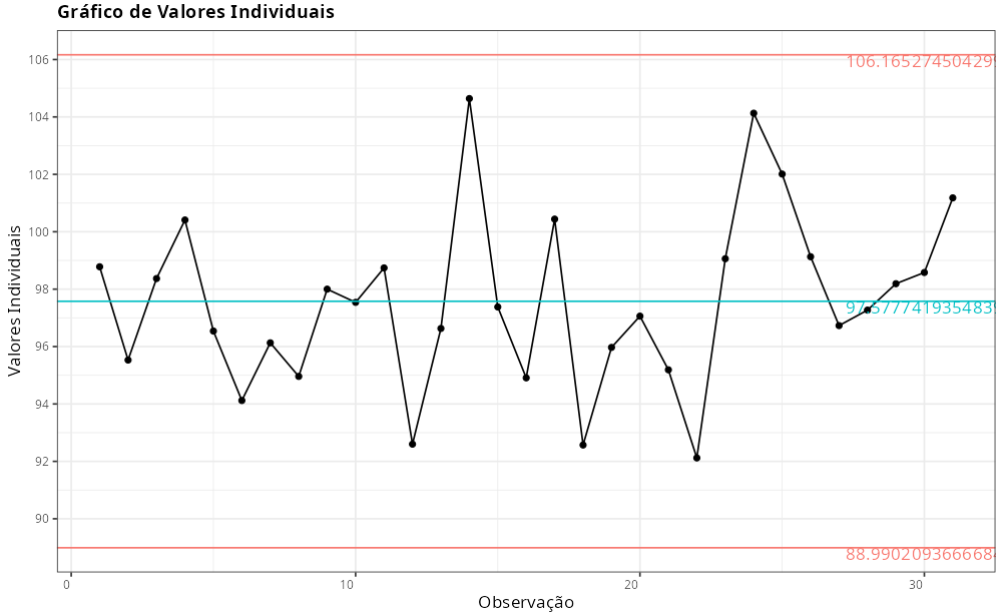
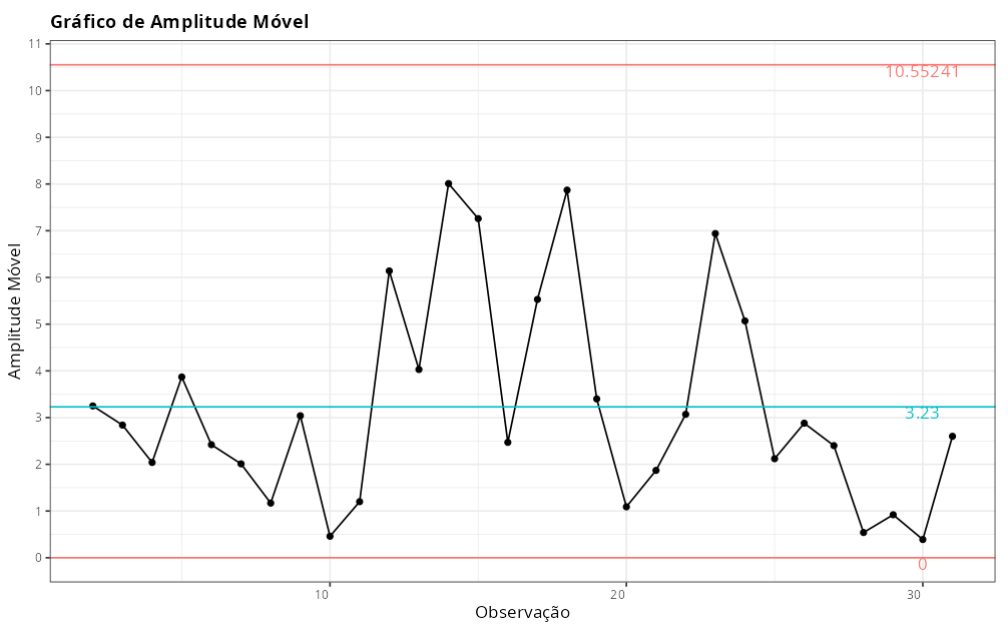
Gráfico de Amplitude Móvel
| Valor | |
|---|---|
| Limite Inferior de Controle | 0 |
| Linha de Centro | 3.23 |
| Limite Superior de Controle | 10.5524 |
Exemplo 2:
Um analista mediu o peso em mg/comprimidos de uma substância em 30 lotes divididos em subgrupos de 3 unidades cada. Foram definidas as especificações LIE = 173 mg e LSE = 187 mg. O objetivo é gerar um relatório estatístico completo para revisar o processo:
| Lotes | Peso |
|---|---|
| 2024001 | 174,8 |
| 2024001 | 176,7 |
| 2024001 | 176,6 |
| 2024002 | 177,7 |
| 2024002 | 181,2 |
| 2024002 | 181,9 |
| 2024003 | 180,3 |
| 2024003 | 179,8 |
| 2024003 | 179,0 |
| 2024004 | 176,3 |
| 2024004 | 178,5 |
| 2024004 | 180,1 |
| 2024005 | 179,6 |
| 2024005 | 180,6 |
| 2024005 | 178,8 |
| 2024006 | 174,4 |
| 2024006 | 177,4 |
| 2024006 | 178,8 |
| 2024007 | 176,3 |
| 2024007 | 178,0 |
| 2024007 | 179,6 |
| 2024008 | 180,0 |
| 2024008 | 179,2 |
| 2024008 | 177,4 |
| 2024009 | 178,1 |
| 2024009 | 178,1 |
| 2024009 | 179,3 |
| 2024010 | 179,3 |
| 2024010 | 181,5 |
| 2024010 | 178,4 |
| 2024011 | 180,9 |
| 2024011 | 180,6 |
| 2024011 | 179,5 |
| 2024012 | 178,7 |
| 2024012 | 178,6 |
| 2024012 | 179,8 |
| 2024013 | 175,3 |
| 2024013 | 180,0 |
| 2024013 | 178,0 |
| 2024014 | 179,8 |
| 2024014 | 180,7 |
| 2024014 | 181,2 |
| 2024015 | 181,0 |
| 2024015 | 178,2 |
| 2024015 | 176,5 |
| 2024016 | 176,4 |
| 2024016 | 176,5 |
| 2024016 | 178,4 |
| 2024017 | 184,8 |
| 2024017 | 183,2 |
| 2024017 | 177,6 |
| 2024018 | 176,9 |
| 2024018 | 176,0 |
| 2024018 | 177,0 |
| 2024019 | 176,9 |
| 2024019 | 178,5 |
| 2024019 | 178,9 |
| 2024020 | 177,4 |
| 2024020 | 177,7 |
| 2024020 | 178,6 |
| 2024021 | 180,3 |
| 2024021 | 179,4 |
| 2024021 | 179,1 |
| 2024022 | 178,3 |
| 2024022 | 176,1 |
| 2024022 | 175,0 |
| 2024023 | 176,2 |
| 2024023 | 179,9 |
| 2024023 | 181,1 |
| 2024024 | 178,2 |
| 2024024 | 179,4 |
| 2024024 | 178,5 |
| 2024025 | 178,3 |
| 2024025 | 176,9 |
| 2024025 | 178,0 |
| 2024026 | 180,6 |
| 2024026 | 177,0 |
| 2024026 | 176,8 |
| 2024027 | 178,0 |
| 2024027 | 178,6 |
| 2024027 | 179,8 |
| 2024028 | 178,5 |
| 2024028 | 180,6 |
| 2024028 | 179,2 |
| 2024029 | 179,1 |
| 2024029 | 176,9 |
| 2024029 | 177,6 |
| 2024030 | 177,5 |
| 2024030 | 178,0 |
| 2024030 | 178,5 |
Faremos o upload dos dados ao sistema:
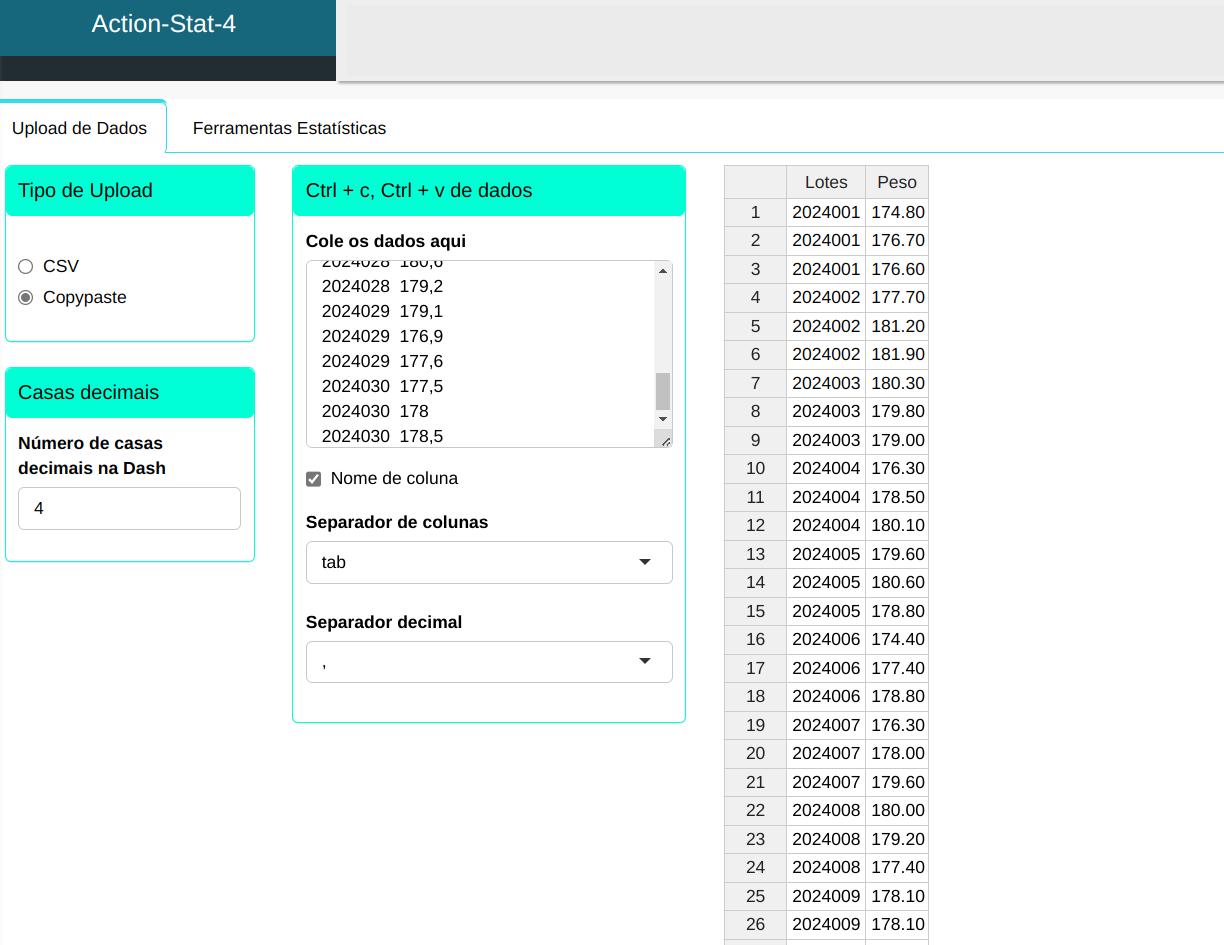
Para realizar a análise configurando conforme a figura abaixo.
Clique em Calcular para obter os resultados. Também pode gerar as análises e baixá-la em formato Word.
Os resultados são:
Resumo Descritivo
| Estatísticas | |
|---|---|
| Mínimo | 174.4 |
| 1º Quantil | 177.4 |
| Média | 178.5856 |
| Mediana | 178.5 |
| Tri-Média | 178.5486 |
| 3º Quantil | 179.8 |
| Máximo | 184.8 |
| Desvio-Padrão | 1.8197 |
| Coeficiente de variação (%) | 1.0189 |
| Assimetría | 0.3461 |
| Curtose | 0.6338 |
| Amplitude | 10.4 |
| Tamanho da Amostra | 90 |
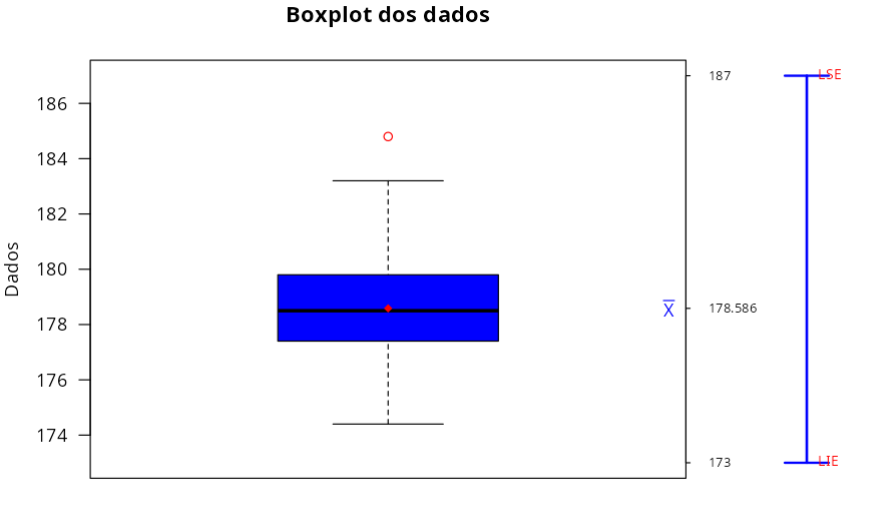
Outliers
| Ordem de Recoleta | Dados | |
|---|---|---|
| 1 | 17 | 184.8 |
Análise Automática
| Análise do Processo | Situação | |
|---|---|---|
| 1 | Teste de Normalidade | Aceita ao nível de significância de 0.05 |
| 2 | Transformação de Box-Cox | Não Aplicável |
| 3 | Transformação de Johnson | Não Aplicável |
| 4 | Distribuição Não Normal | Não Aplicável |
| 5 | Distribuição Não Paramêtrica | Não Aplicável |
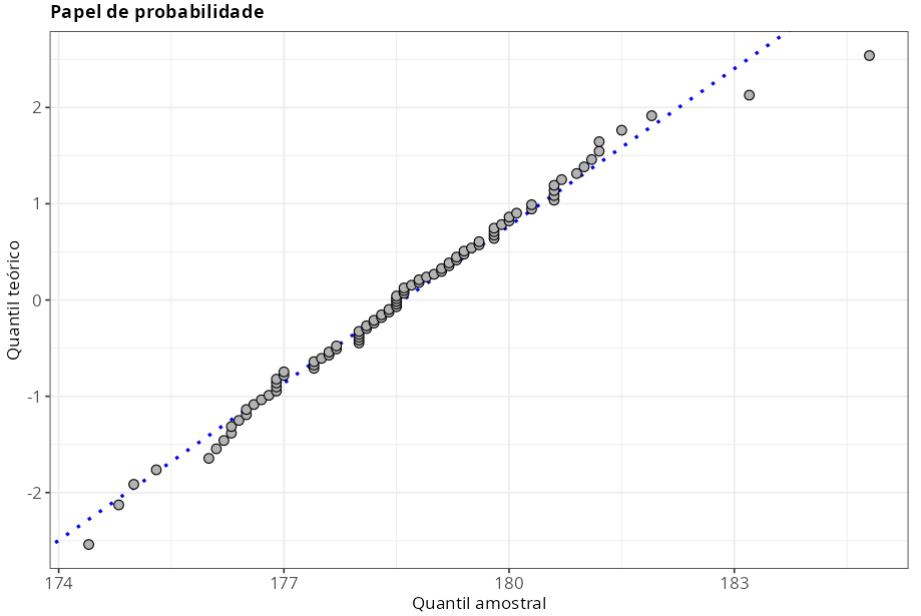
Teste de Normalidade
| Estatística | P-Valor | |
|---|---|---|
| Anderson Darling | 0.2273 | 0.8093 |
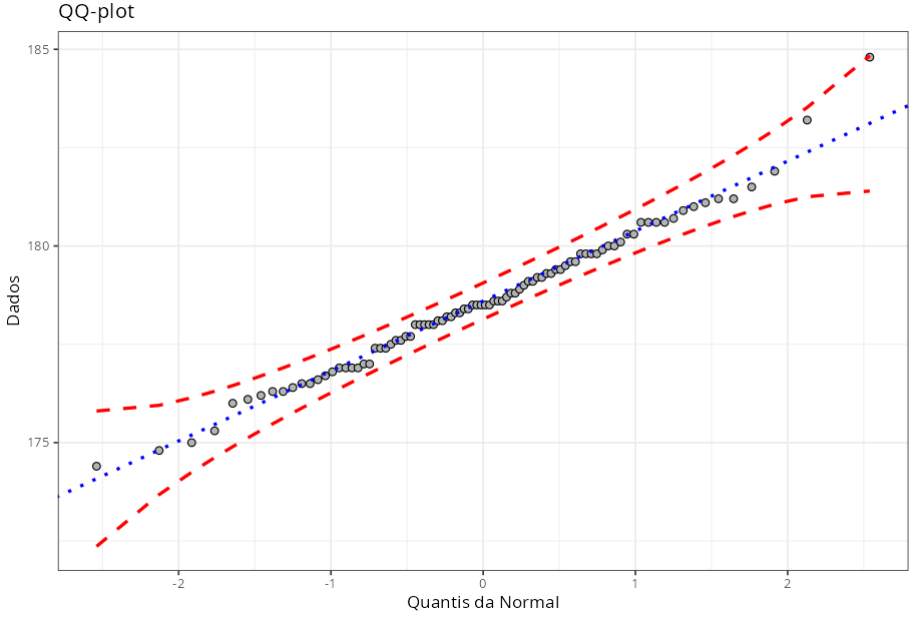
Especificações
| Valor | ||
|---|---|---|
| 1 | Amostra | 90 |
| 2 | Limite Inferior | 173 |
| 3 | Limite Superiior | 187 |
Estimativas
| Valor | |
|---|---|
| Média | 178.5856 |
| Desvio-Padrão (Curto prazo) | 1.5184 |
| Desvio_Padrão (Longo prazo) | 1.8197 |
Índices de performance (Longo Prazo)
| Índices de Performance - (Variabilidade Total) | |
|---|---|
| PP | 1.2823 |
| PPI | 1.0232 |
| PPS | 1.5414 |
| PPK | 1.0232 |
Índices de Capacidade (Curto Prazo)
| Índices de Capacidade - Variabilidade Inerente | |
|---|---|
| CP | 1.5367 |
| CPI | 1.2262 |
| CPS | 1.8472 |
| CPK | 1.2262 |
Índices Observados
| Índices Observados | |
|---|---|
| PPM < LIE | 0 |
| PPM > LSE | 0 |
| PPM Total | 0 |
Índices Esperados (Longo Prazo)
| Índices Esperados (Variabilidade Total) | |
|---|---|
| PPM < LIE | 1071.8298 |
| PPM > LSE | 1.8802 |
| PPM Total | 1073.7100 |
Índices Esperados (Curto prazo)
| Índices Esperados (Variabilidade Inerente) | |
|---|---|
| PPM < LIE | 117.2693 |
| PPM > LSE | 0.0150 |
| PPM Total | 117.2843 |
NÍVEL SIGMA
| Nível SIGMA | |
|---|---|
| Zbench (longo prazo) | 3.069 |
| Zbench (curto prazo) | 3.6785 |
| Zshift | 1.5 |
| Métrica Sigma | 4.569 |
Análise Gráfico
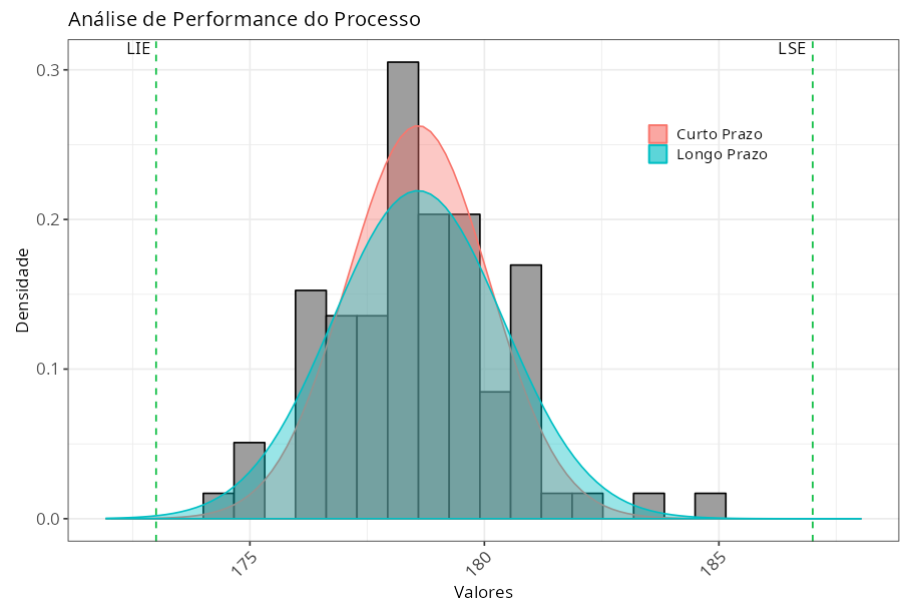
Estabilidade do Processo - Gráficos de Médias e Amplitude
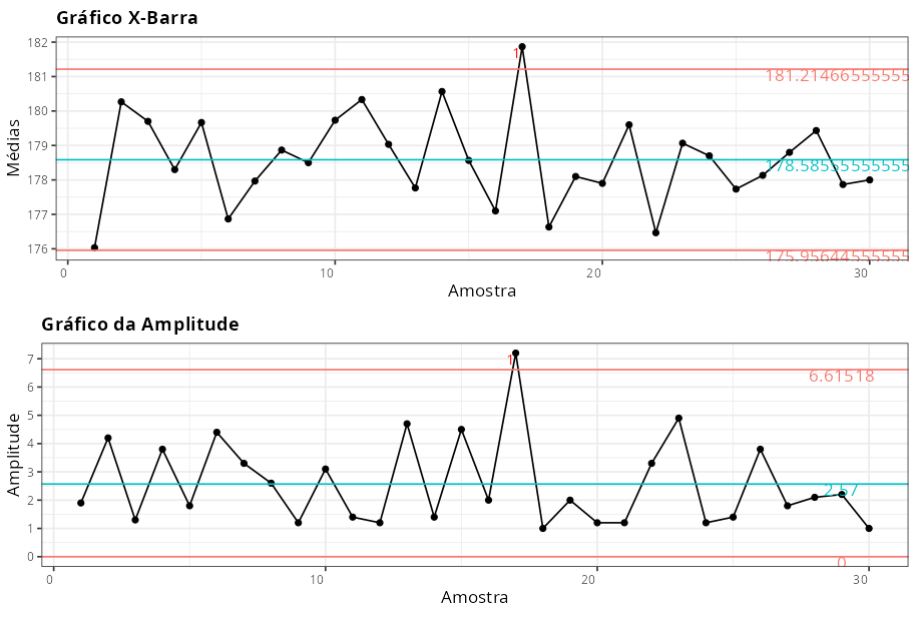
Gráfico X-Barra
| Valor | |
|---|---|
| Limite Inferior de Controle | 175.9564 |
| Linha de centro | 178.5856 |
| Limite Superior de Controle | 181.2147 |
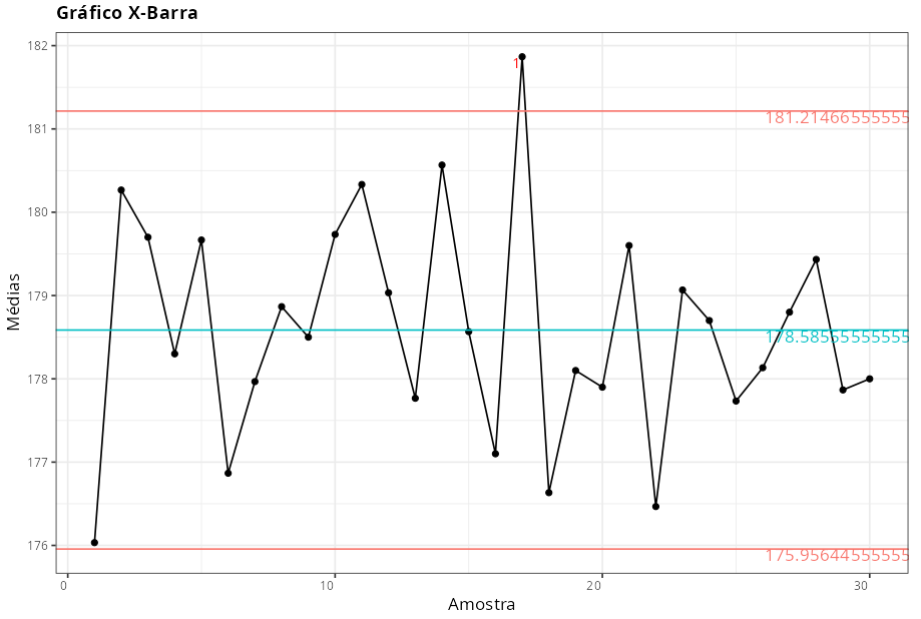
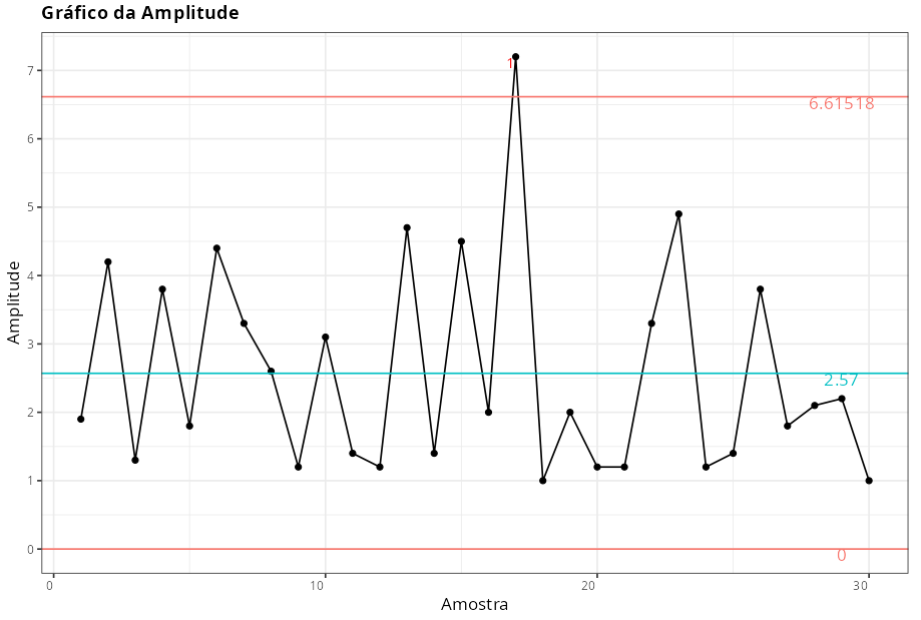
Gráfico Amplitude
| Valor | |
|---|---|
| Limite Inferior de Controle | 0 |
| Linha de centro | 2.57 |
| Limite Superior de Controle | 6.6152 |
Exemplo 3:
Um analista mediu o peso em mg/comprimido de uma substância para 10 lotes, divididos em subgrupos de tamanho 10. Foram definidas as especificações LIE = 13 e LSE = 15. O objetivo é gerar um relatório estatístico completo para revisar o processo:
| Lote | Dureza | Lote | Dureza |
|---|---|---|---|
| 2024001 | 13,06 | 2024009 | 13,61 |
| 2024001 | 13,12 | 2024009 | 13,71 |
| 2024001 | 13,20 | 2024009 | 13,79 |
| 2024001 | 13,21 | 2024009 | 13,82 |
| 2024001 | 13,28 | 2024009 | 14,18 |
| 2024001 | 13,37 | 2024009 | 14,25 |
| 2024001 | 13,39 | 2024009 | 14,26 |
| 2024001 | 13,41 | 2024009 | 14,29 |
| 2024001 | 13,43 | 2024009 | 14,53 |
| 2024001 | 13,48 | 2024009 | 13,12 |
| 2024002 | 13,58 | 2024010 | 13,20 |
| 2024002 | 13,61 | 2024010 | 13,21 |
| 2024002 | 13,71 | 2024010 | 13,30 |
| 2024002 | 13,79 | 2024010 | 13,37 |
| 2024002 | 13,82 | 2024010 | 13,41 |
| 2024002 | 14,18 | 2024010 | 13,45 |
| 2024002 | 14,25 | 2024010 | 13,53 |
| 2024002 | 14,26 | 2024010 | 13,57 |
| 2024002 | 14,29 | 2024010 | 13,80 |
| 2024002 | 14,53 | 2024010 | 13,81 |
| 2024003 | 13,12 | 2024011 | 13,82 |
| 2024003 | 13,20 | 2024011 | 14,09 |
| 2024003 | 13,21 | 2024011 | 13,06 |
| 2024003 | 13,30 | 2024011 | 13,12 |
| 2024003 | 13,37 | 2024011 | 13,20 |
| 2024003 | 13,41 | 2024011 | 13,21 |
| 2024003 | 13,45 | 2024011 | 13,28 |
| 2024003 | 13,53 | 2024011 | 13,37 |
| 2024003 | 13,57 | 2024011 | 13,39 |
| 2024003 | 13,80 | 2024011 | 13,41 |
| 2024004 | 13,81 | 2024012 | 13,43 |
| 2024004 | 13,82 | 2024012 | 13,48 |
| 2024004 | 14,09 | 2024012 | 13,58 |
| 2024004 | 14,13 | 2024012 | 13,61 |
| 2024004 | 14,18 | 2024012 | 13,71 |
| 2024004 | 14,35 | 2024012 | 13,79 |
| 2024004 | 13,06 | 2024012 | 13,82 |
| 2024004 | 13,12 | 2024012 | 14,18 |
| 2024004 | 13,20 | 2024012 | 14,25 |
| 2024004 | 13,21 | 2024012 | 14,26 |
| 2024005 | 13,37 | 2024013 | 14,29 |
| 2024005 | 13,39 | 2024013 | 14,53 |
| 2024005 | 13,41 | 2024013 | 13,12 |
| 2024005 | 13,43 | 2024013 | 13,20 |
| 2024005 | 13,48 | 2024013 | 13,21 |
| 2024005 | 13,58 | 2024013 | 13,30 |
| 2024005 | 13,61 | 2024013 | 13,37 |
| 2024005 | 13,71 | 2024013 | 13,41 |
| 2024005 | 13,79 | 2024013 | 13,45 |
| 2024005 | 13,82 | 2024013 | 13,53 |
| 2024006 | 14,18 | 2024014 | 13,57 |
| 2024006 | 14,25 | 2024014 | 13,80 |
| 2024006 | 14,26 | 2024014 | 13,81 |
| 2024006 | 14,29 | 2024014 | 13,82 |
| 2024006 | 14,53 | 2024014 | 14,09 |
| 2024006 | 13,12 | 2024014 | 14,13 |
| 2024006 | 13,20 | 2024014 | 14,18 |
| 2024006 | 13,21 | 2024014 | 14,35 |
| 2024006 | 13,30 | 2024014 | 13,06 |
| 2024006 | 13,37 | 2024014 | 13,12 |
| 2024007 | 13,41 | 2024015 | 13,20 |
| 2024007 | 13,45 | 2024015 | 13,21 |
| 2024007 | 13,53 | 2024015 | 13,28 |
| 2024007 | 13,57 | 2024015 | 13,06 |
| 2024007 | 13,80 | 2024015 | 13,12 |
| 2024007 | 13,81 | 2024015 | 13,20 |
| 2024007 | 13,82 | 2024015 | 13,21 |
| 2024007 | 14,09 | 2024015 | 13,28 |
| 2024007 | 14,13 | 2024015 | 13,37 |
| 2024007 | 13,06 | 2024015 | 13,39 |
| 2024008 | 13,12 | 2024016 | 13,41 |
| 2024008 | 13,20 | 2024016 | 13,43 |
| 2024008 | 13,21 | 2024016 | 13,48 |
| 2024008 | 13,28 | 2024016 | 13,58 |
| 2024008 | 13,37 | 2024016 | 13,61 |
| 2024008 | 13,39 | 2024016 | 13,71 |
| 2024008 | 13,41 | 2024016 | 13,79 |
| 2024008 | 13,43 | 2024016 | 13,82 |
| 2024008 | 13,48 | 2024016 | 14,18 |
| 2024008 | 13,58 | 2024016 | 13,28 |
Faremos o upload dos dados no sistema.
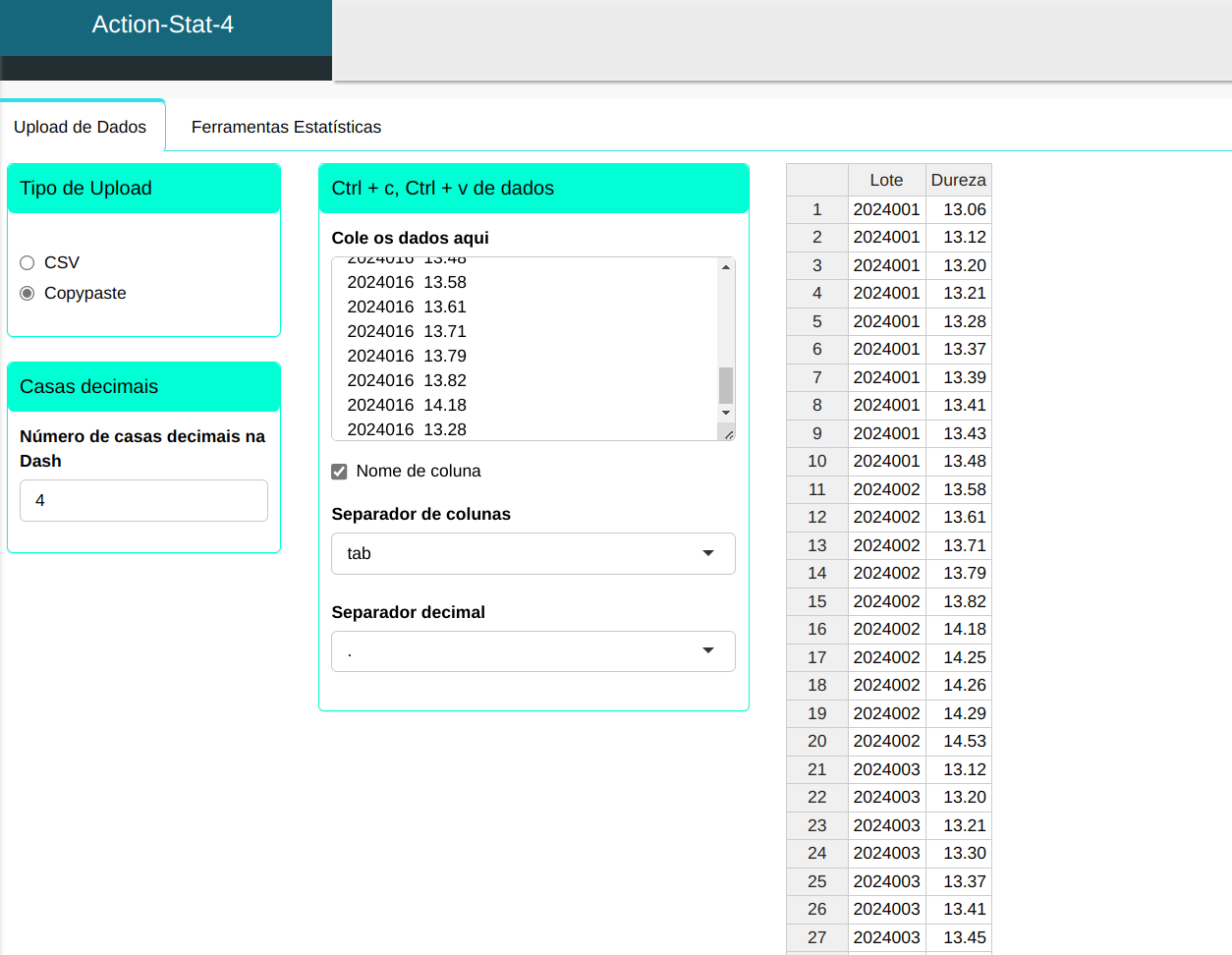
Para realizar a análise configurando conforme a figura abaixo.
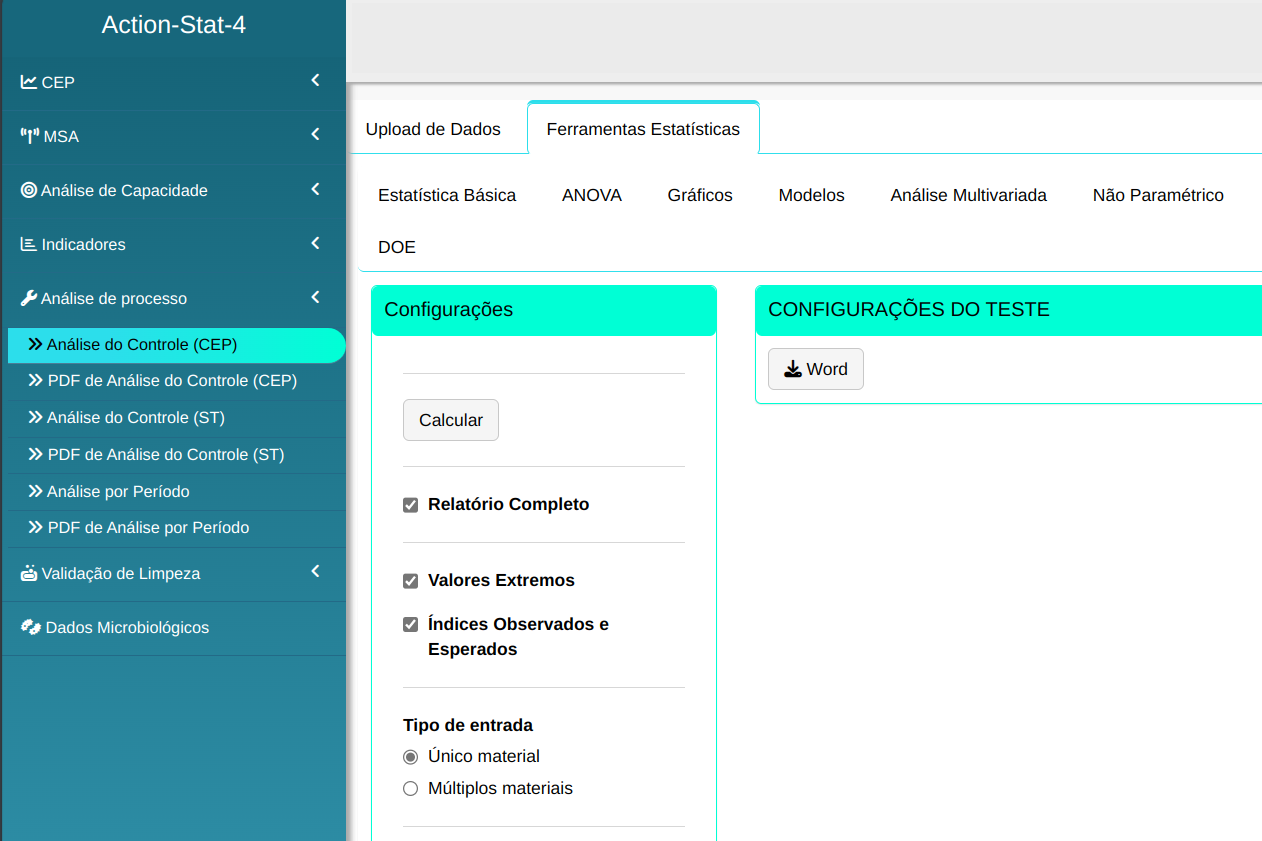
Em seguida, clique em Calcular para obter os resultados. Também pode gerar as análises e baixar em formato Word.
Os resultados são:
Resumo Descritivo
| Estatísticas | |
|---|---|
| Mínimo | 13.06 |
| 1º Quantil | 13.28 |
| Média | 13.5972 |
| Mediana | 13.48 |
| Tri-Média | 13.5662 |
| 3º Quantil | 13.82 |
| Máximo | 14.53 |
| Desvio-Padrão | 0.3933 |
| Coeficiente de variação (%) | 2.8924 |
| Assimetría | 0.6638 |
| Curtose | -0.6347 |
| Amplitude | 1.47 |
| Tamanho da Amostra | 160 |
Análise Automático
| Análise de Processo | Situação | |
|---|---|---|
| 1 | Teste de Normalidade | Hipótese de normalidade rejeitada ao nível de significância de 5% |
| 2 | Transformação de Box-Cox | Não foi possível utilizar a transformação de Box-Cox |
| 3 | Transformação de Johnson | Não foi possível utilizar a transformação de Johnson |
| 4 | Distribuição Não Normal | Não foi possível utilizar outras distribuições paramétricas |
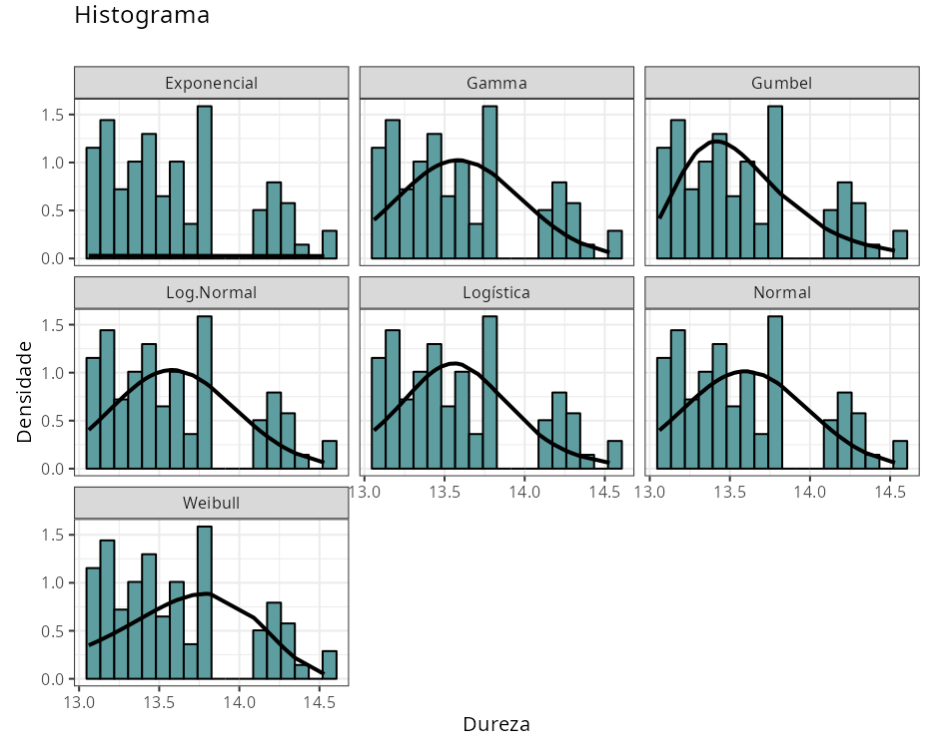
| 5 | Distribuições Não Paramétrica | O método não paramétrico de Kernel foi utilizdo para o ajuste dos dados |
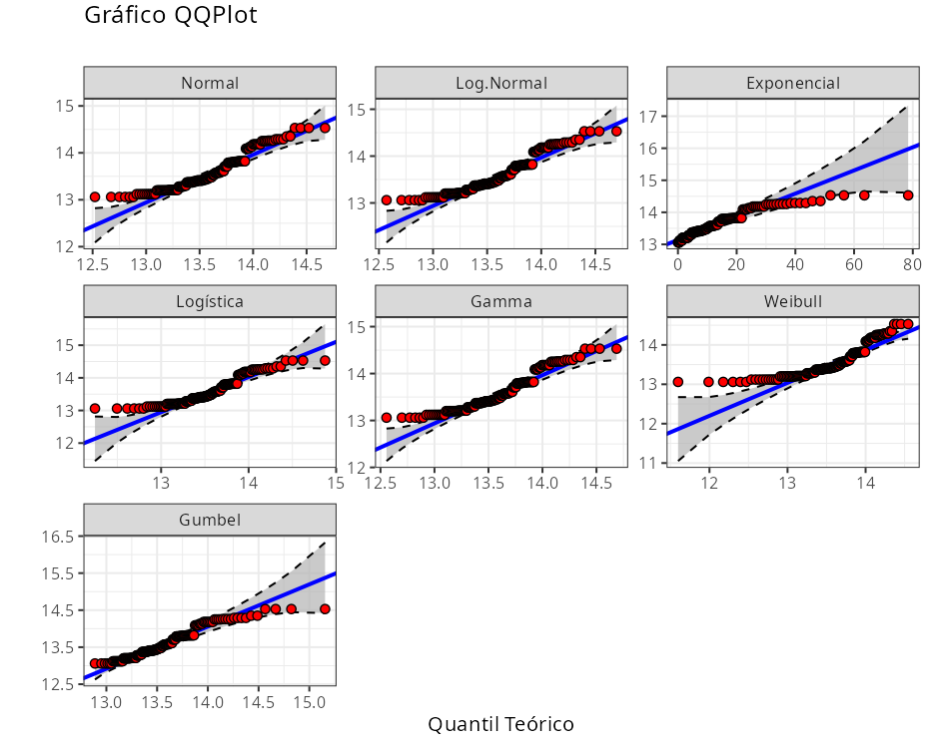
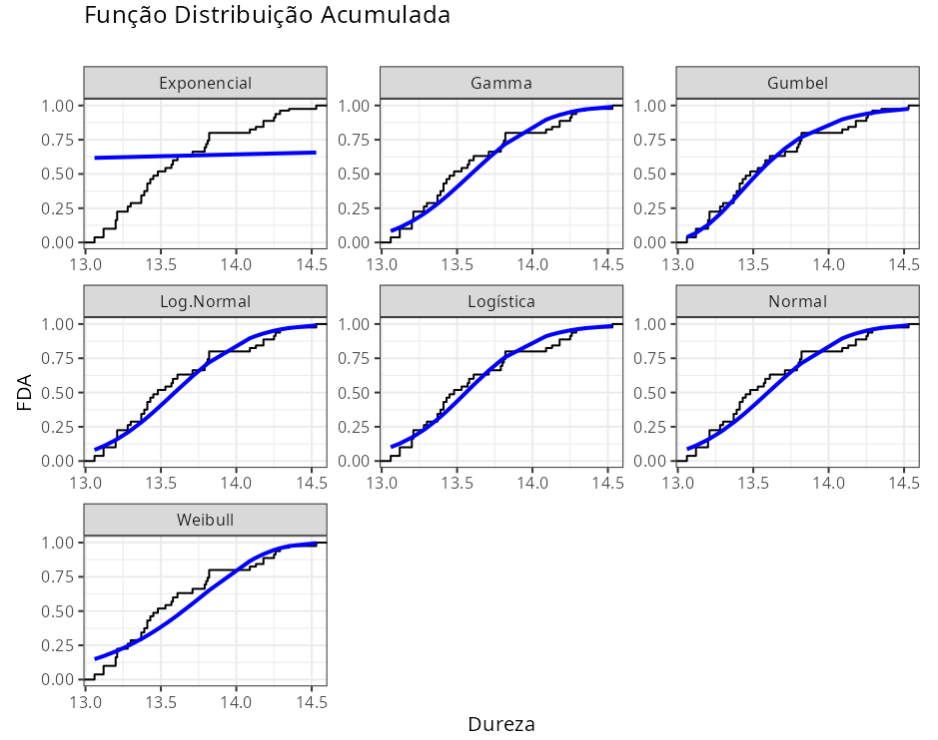
Anderson-Darling
| Distribuições | Estatística | P-Valor | |
|---|---|---|---|
| 1 | Normal ($\mu$ = 13.6, $\sigma$ = 0.39) | 4.3496 | 0 |
| 2 | Log-Normal(log($\mu$) = 2.60946, log($\sigma$) = 0.0285766) | 4.0776 | 0 |
| 3 | Exponencial(Taxa = 0.0735443) | 69.3914 | 0 |
| 4 | Logística(Locação = 13.56, Escala = 0.23) | 3.8440 | 0.005 |
| 5 | Gamma(Forma = 1217.62, Tasa = 89.5491) | 4.1954 | 0.0050 |
| 6 | Weibull(Forma = 33.1981, Escala = 13.7979) | 7.0015 | 0.01 |
| 7 | Gumbel(Locação = 13.416, Escala = 0.301584) | 2.0802 | 0.01 |
Estabilidade do Processo
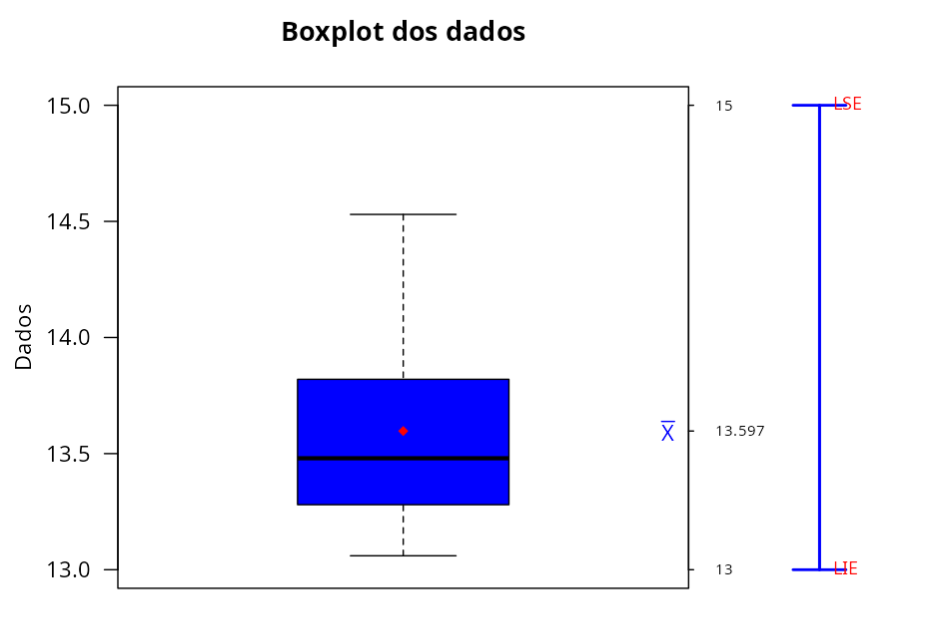
Especificações
| Valor | ||
|---|---|---|
| 1 | Amostra | 160 |
| 2 | Limite Inferior | 13 |
| 3 | Limite Superior | 15 |
Estimativas
| Parâmetros | Valor | |
|---|---|---|
| 1 | Média | 13.59725 |
| 2 | Desvio Padrão | 0.393291144736697 |
Índices de Performance
| Índices de Rendimento | ||
|---|---|---|
| 1 | PP | 1.0353 |
| 2 | PPI | 0.7232 |
| 3 | PPS | 1.2156 |
| 4 | PPK | 0.7232 |
Índices Observados
| Índices Obsevados | ||
|---|---|---|
| 1 | PPM > LSE | 0 |
| 2 | PPM < LIE | 0 |
Índices Esperados
| Índices Esperados | ||
|---|---|---|
| 1 | PPM > LSE | 0 |
| 2 | PPM < LIE | 30774.1006085405 |
| 3 | PPM Total | 30774.1006085405 |
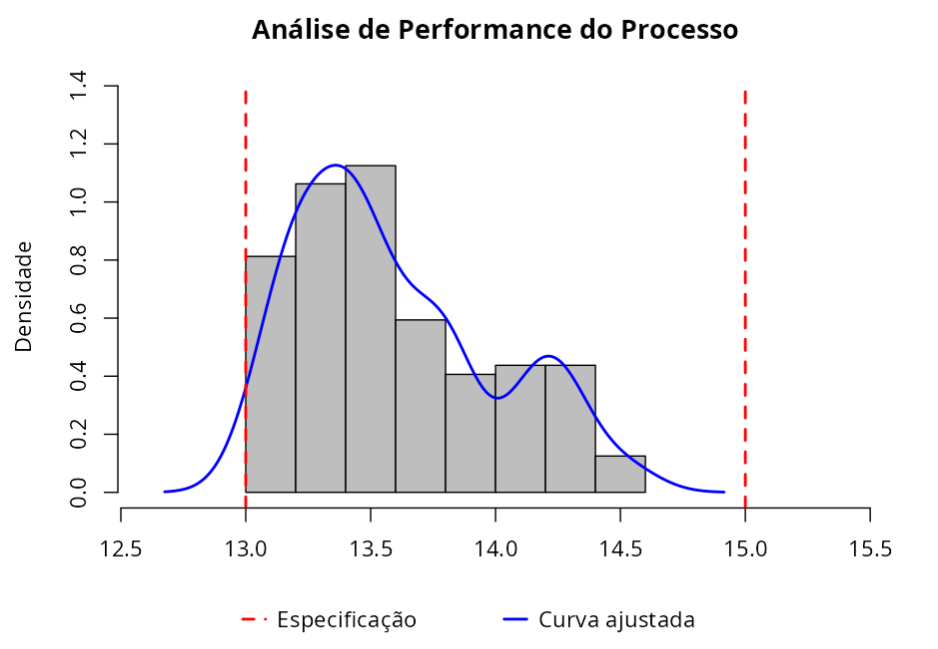
Qualidade do Ajuste (Não Paramétrico - Núcleo: Método Gaussian)
| Método | Estatística | P-valor | |
|---|---|---|---|
| Cramér-von Mises | gaussian | 0.0929 | 0.7652 |
| Kolmogorov-Smirnov | gaussian | 0.0750 | 0.7591 |
Teste de Normalidade (Outliers)
| Obs. | Quantis da Normal | Dados | Critério | |
|---|---|---|---|---|
| 1 | 1 | -2.73 | 13.06 | Envelope (Nível de Confiança=95%) |
| 2 | 43 | -2.35 | 13.06 | Envelope (Nível de Confiança=95%) |
| 3 | 63 | -2.15 | 13.06 | Envelope (Nível de Confiança=95%) |
| 4 | 100 | -2.02 | 13.06 | Envelope (Nível de Confiança=95%) |
| 5 | 142 | -1.91 | 13.06 | Envelope (Nível de Confiança=95%) |
| 6 | 151 | -1.82 | 13.06 | Envelope (Nível de Confiança=95%) |
| 7 | 3 | -1.74 | 13.12 | Envelope (Nível de Confiança=95%) |
| 8 | 8 | -1.68 | 13.12 | Envelope (Nível de Confiança=95%) |
| 9 | 17 | -1.62 | 13.12 | Envelope (Nível de Confiança=95%) |
| 10 | 45 | -1.56 | 13.12 | Envelope (Nível de Confiança=95%) |
| 11 | 59 | -1.51 | 13.12 | Envelope (Nível de Confiança=95%) |
| 12 | 79 | -1.46 | 13.12 | Envelope (Nível de Confiança=95%) |
| 13 | 86 | -1.42 | 13.12 | Envelope (Nível de Confiança=95%) |
| 14 | 116 | -1.38 | 13.12 | Envelope (Nível de Confiança=95%) |
| 15 | 10 | -1.26 | 13.2 | Envelope (Nível de Confiança=95%) |
| 16 | 15 | -1.23 | 13.2 | Envelope (Nível de Confiança=95%) |
| 17 | 19 | -1.2 | 13.2 | Envelope (Nível de Confiança=95%) |
| 18 | 24 | -1.17 | 13.2 | Envelope (Nível de Confiança=95%) |
| 19 | 33 | -1.14 | 13.2 | Envelope (Nível de Confiança=95%) |
| 20 | 27 | 0.85 | 14.09 | Envelope (Nível de Confiança=95%) |
| 21 | 36 | 0.88 | 14.09 | Envelope (Nível de Confiança=95%) |
| 22 | 78 | 0.9 | 14.09 | Envelope (Nível de Confiança=95%) |
| 23 | 119 | 0.92 | 14.09 | Envelope (Nível de Confiança=95%) |
| 24 | 52 | 0.95 | 14.13 | Envelope (Nível de Confiança=95%) |
| 25 | 94 | 0.97 | 14.13 | Envelope (Nível de Confiança=95%) |
| 26 | 135 | 1 | 14.13 | Envelope (Nível de Confiança=95%) |
| 27 | 6 | 1.02 | 14.18 | Envelope (Nível de Confiança=95%) |
| 28 | 68 | 1.05 | 14.18 | Envelope (Nível de Confiança=95%) |
| 29 | 73 | 1.08 | 14.18 | Envelope (Nível de Confiança=95%) |
| 30 | 82 | 1.11 | 14.18 | Envelope (Nível de Confiança=95%) |
| 31 | 110 | 1.14 | 14.18 | Envelope (Nível de Confiança=95%) |
| 32 | 124 | 1.17 | 14.18 | Envelope (Nível de Confiança=95%) |
| 33 | 144 | 1.2 | 14.18 | Envelope (Nível de Confiança=95%) |
| 34 | 22 | 1.23 | 14.25 | Envelope (Nível de Confiança=95%) |
| 35 | 89 | 1.26 | 14.25 | Envelope (Nível de Confiança=95%) |
| 36 | 98 | 1.3 | 14.25 | Envelope (Nível de Confiança=95%) |
| 37 | 140 | 1.34 | 14.25 | Envelope (Nível de Confiança=95%) |
| 38 | 38 | 1.38 | 14.26 | Envelope (Nível de Confiança=95%) |
| 39 | 105 | 1.42 | 14.26 | Envelope (Nível de Confiança=95%) |
| 40 | 114 | 1.46 | 14.26 | Envelope (Nível de Confiança=95%) |
| 41 | 129 | -0.1 | 13.43 | Envelope (Nível de Confiança=95%) |
| 42 | 99 | -0.05 | 13.45 | Envelope (Nível de Confiança=95%) |
| 43 | 141 | -0.04 | 13.45 | Envelope (Nível de Confiança=95%) |
| 44 | 136 | 0.02 | 13.48 | Envelope (Nível de Confiança=95%) |
| 45 | 145 | 0.04 | 13.48 | Envelope (Nível de Confiança=95%) |
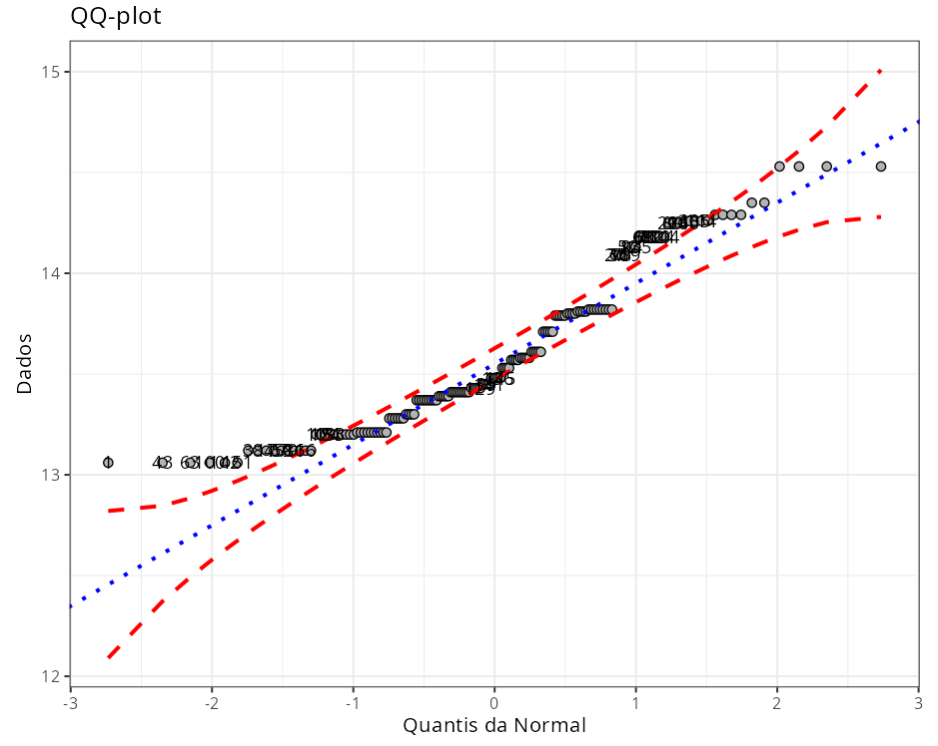
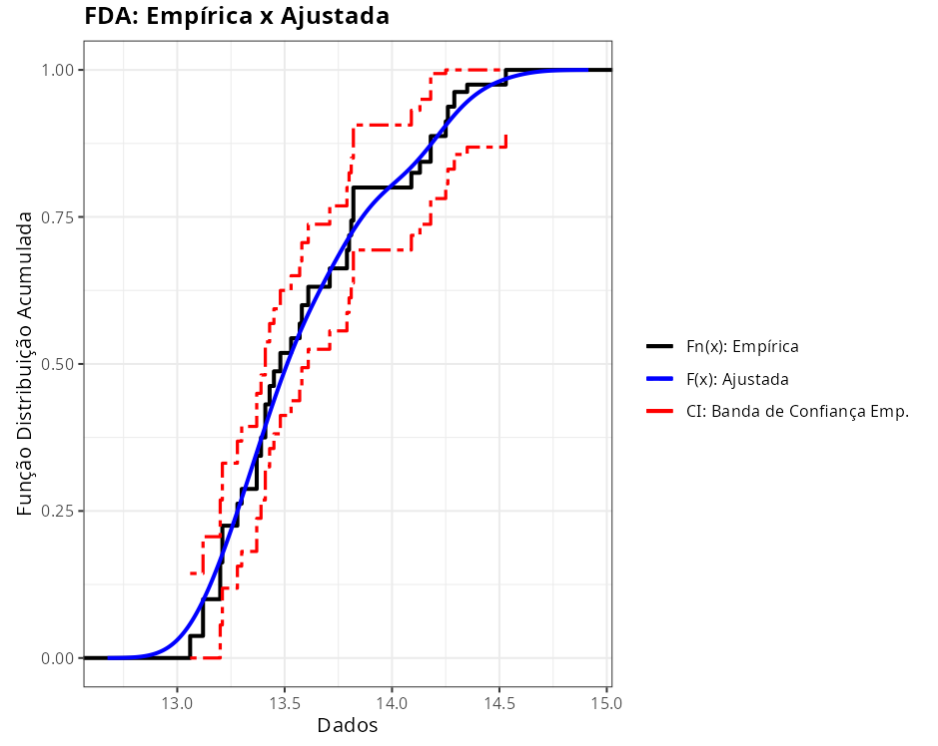
Nenhuma das distribuições consideradas pode ser usada para modelar a distribuição de dados.
Estabilidade do Processo
Gráfico de X-Barra e Desvio-Padrão
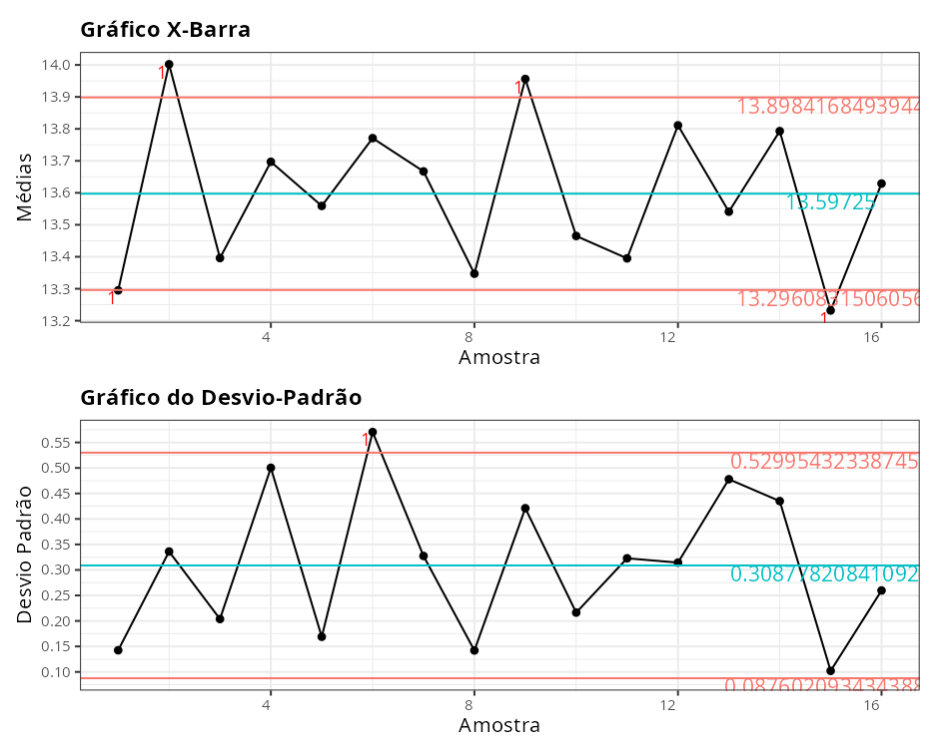
Gráfico de X-Barra
| Valor | |
|---|---|
| Limite Inferior de Controle | 13.2961 |
| Linha Central | 13.5972 |
| Limite Superior de controle | 13.8984 |
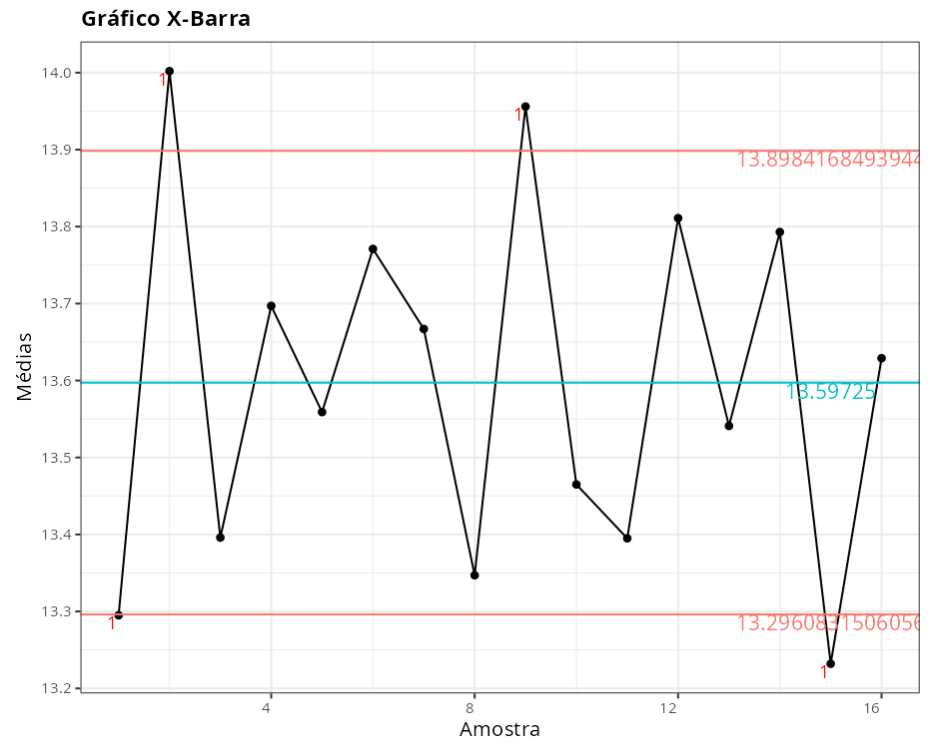
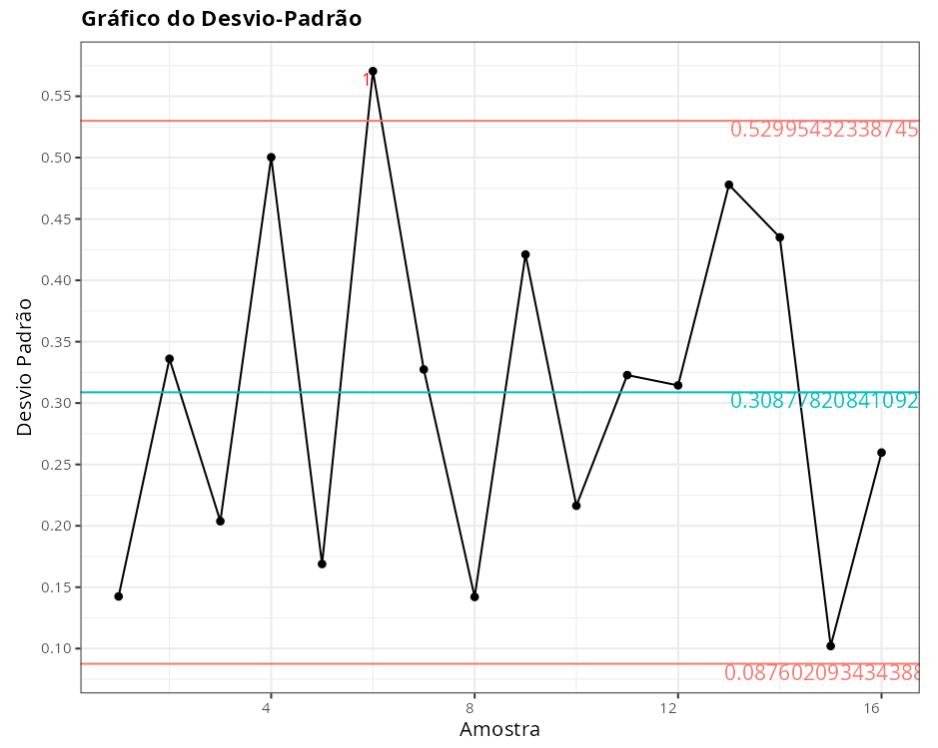
Gráfico de Desvio-Padrão
| Valor | |
|---|---|
| Limite Inferior de Controle | 0.0876 |
| Linha Central | 0.3088 |
| Limite Superior de controle | 0.53 |
Teste de Kruskal-Wallis
| Valor | |
|---|---|
| Estadística | 54.2338 |
| Grados de Libertad | 15 |
| P-valor | 0 |
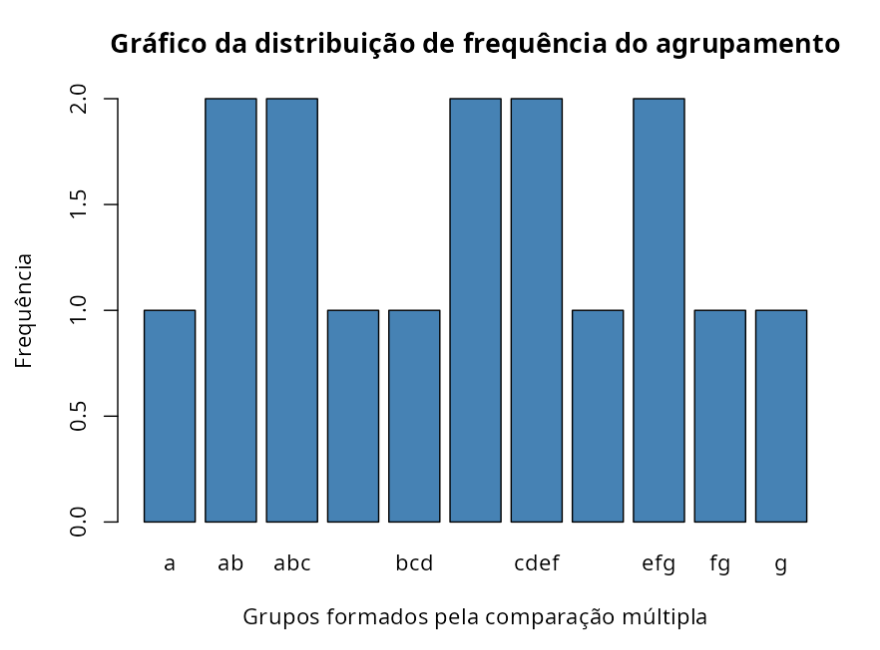
Tabela de Agrupamento da Comparação dos grupos (Kruskal Wallis)
| Fator | Média | Mediana | Média dos Ranks | Grupos |
|---|---|---|---|---|
| 2024002 | 14.0020 | 14.0000 | 127.3000 | a |
| 2024009 | 13.9560 | 14.0000 | 119.0500 | ab |
| 2024012 | 13.8110 | 13.7500 | 111.5000 | ab |
| 2024014 | 13.7930 | 13.8150 | 101.8500 | abc |
| 2024007 | 13.6670 | 13.6850 | 93.9500 | abc |
| 2024016 | 13.6290 | 13.5950 | 92.6500 | abcd |
| 2024006 | 13.7710 | 13.7750 | 90.3000 | bcd |
| 2024004 | 13.6970 | 13.8150 | 86.8500 | bcde |
| 2024005 | 13.5590 | 13.5300 | 85.7000 | bcde |
| 2024013 | 13.5410 | 13.3900 | 69.8000 | cdef |
| 2024010 | 13.4650 | 13.4300 | 69.6000 | cdef |
| 2024003 | 13.3960 | 13.3900 | 59.0000 | defg |
| 2024011 | 13.3950 | 13.3250 | 53.6000 | efg |
| 2024008 | 13.3470 | 13.3800 | 52.5000 | efg |
| 2024001 | 13.2950 | 13.3250 | 43.4500 | fg |
| 2024015 | 13.2320 | 13.2100 | 30.9000 | g |
Tabela da Proporção do Total de Grupos Formados pelo Total de Lote
| Valores | |
|---|---|
| Número de Grupos Formados | 11 |
| Frecuência Total | 16 |
| Proporção de Grupos pelo Total de Lote | 68.75 |