5. Graficos para Pequenos Lotes
Para atingir as eficiências dos processos para pequenos lotes é essencial que os métodos de CEP possam verificar se o processo está verdadeiramente sob controle estatístico, ou seja, se ele é previsível e se pode detectar variações devido às causas especiais durante esses pequenos "lotes".
Exemplo 1:
Na usinagem bruta de diâmetros externos (eixos) em torno mecânico foram retiradas 25 amostras, cada uma constituída de 3 peças, obtendo-se os valores da tabela abaixo.
| Amostra | N | Peca | P1 | P2 | P3 |
|---|---|---|---|---|---|
| 1 | 220 | 1 | 219,7838 | 220,0287 | 220,0922 |
| 2 | 220 | 1 | 219,9046 | 220,1229 | 220,2368 |
| 3 | 220 | 1 | 219,8345 | 220,0862 | 219,9268 |
| 4 | 220 | 1 | 219,7302 | 220,001 | 220,0357 |
| 5 | 220 | 1 | 220,1644 | 220,3151 | 219,9806 |
| 6 | 260 | 2 | 259,8635 | 260,1847 | 259,867 |
| 7 | 260 | 2 | 259,7917 | 259,9042 | 259,908 |
| 8 | 260 | 2 | 259,8264 | 259,8535 | 259,6465 |
| 9 | 260 | 2 | 259,6421 | 260,0869 | 259,9488 |
| 10 | 260 | 2 | 259,8945 | 260,0154 | 260,3685 |
| 11 | 320 | 3 | 319,7366 | 319,5236 | 319,7053 |
| 12 | 320 | 3 | 319,8834 | 319,415 | 319,8163 |
| 13 | 320 | 3 | 320,2431 | 320,1935 | 319,9893 |
| 14 | 320 | 3 | 319,9805 | 320,0828 | 320,0418 |
| 15 | 320 | 3 | 320,4944 | 320,4552 | 320,0477 |
| 16 | 240 | 4 | 239,8076 | 239,7787 | 240,2064 |
| 17 | 240 | 4 | 240,1663 | 240,1888 | 240,2023 |
| 18 | 240 | 4 | 240,1662 | 240,1382 | 240,1141 |
| 19 | 240 | 4 | 240,017 | 239,9212 | 240,0397 |
| 20 | 240 | 4 | 240,2081 | 240,0484 | 239,9119 |
| 21 | 300 | 5 | 300,0479 | 300,1325 | 299,9955 |
| 22 | 300 | 5 | 300,2815 | 299,9451 | 300,0365 |
| 23 | 300 | 5 | 299,7173 | 300,383 | 300,4608 |
| 24 | 300 | 5 | 300,0009 | 300,0487 | 300,0038 |
| 25 | 300 | 5 | 299,5822 | 300,4351 | 299,7919 |

Realizaremos a análise configurando conforme a figura abaixo.
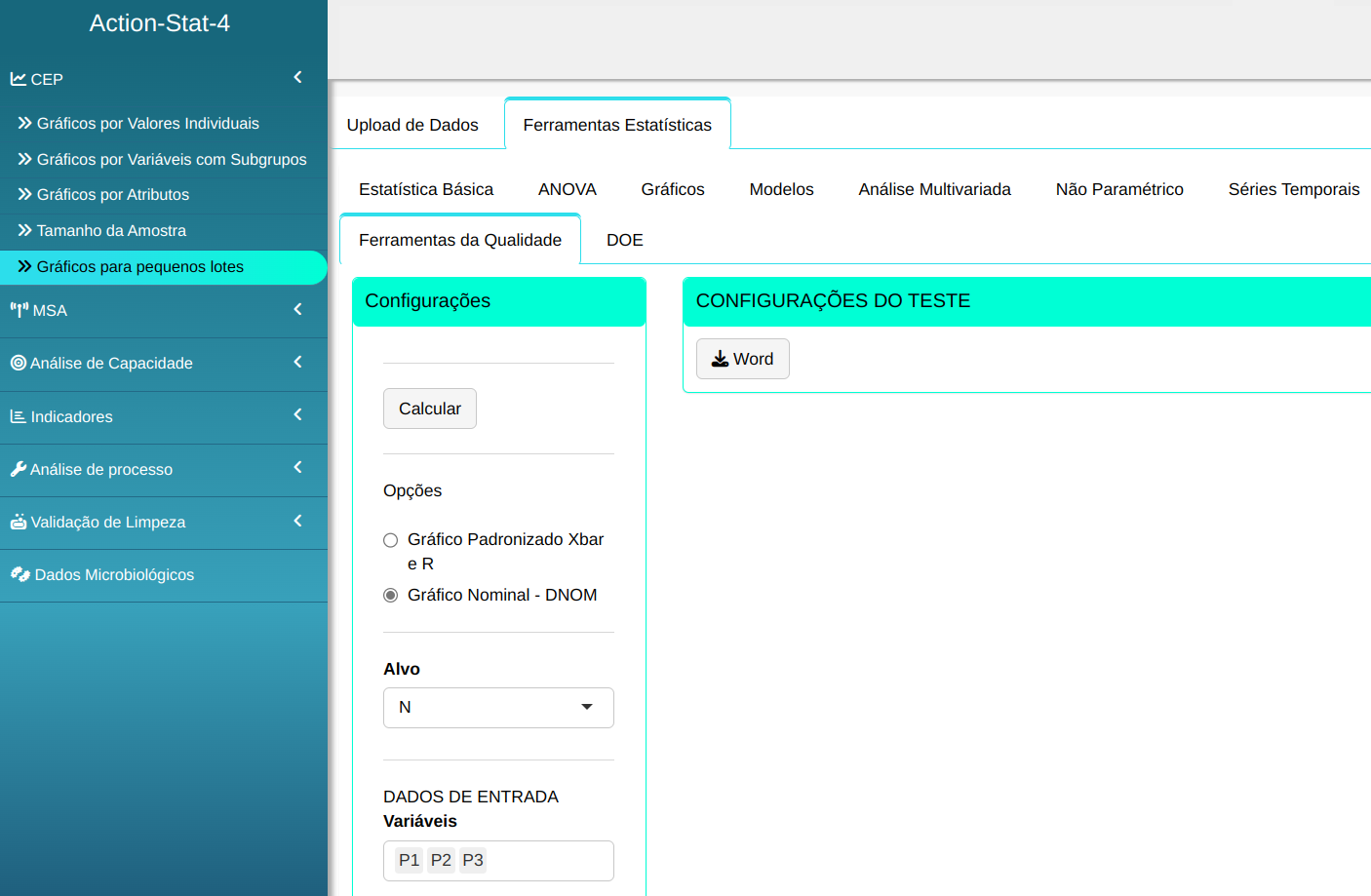

Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e baixar em formato Word.

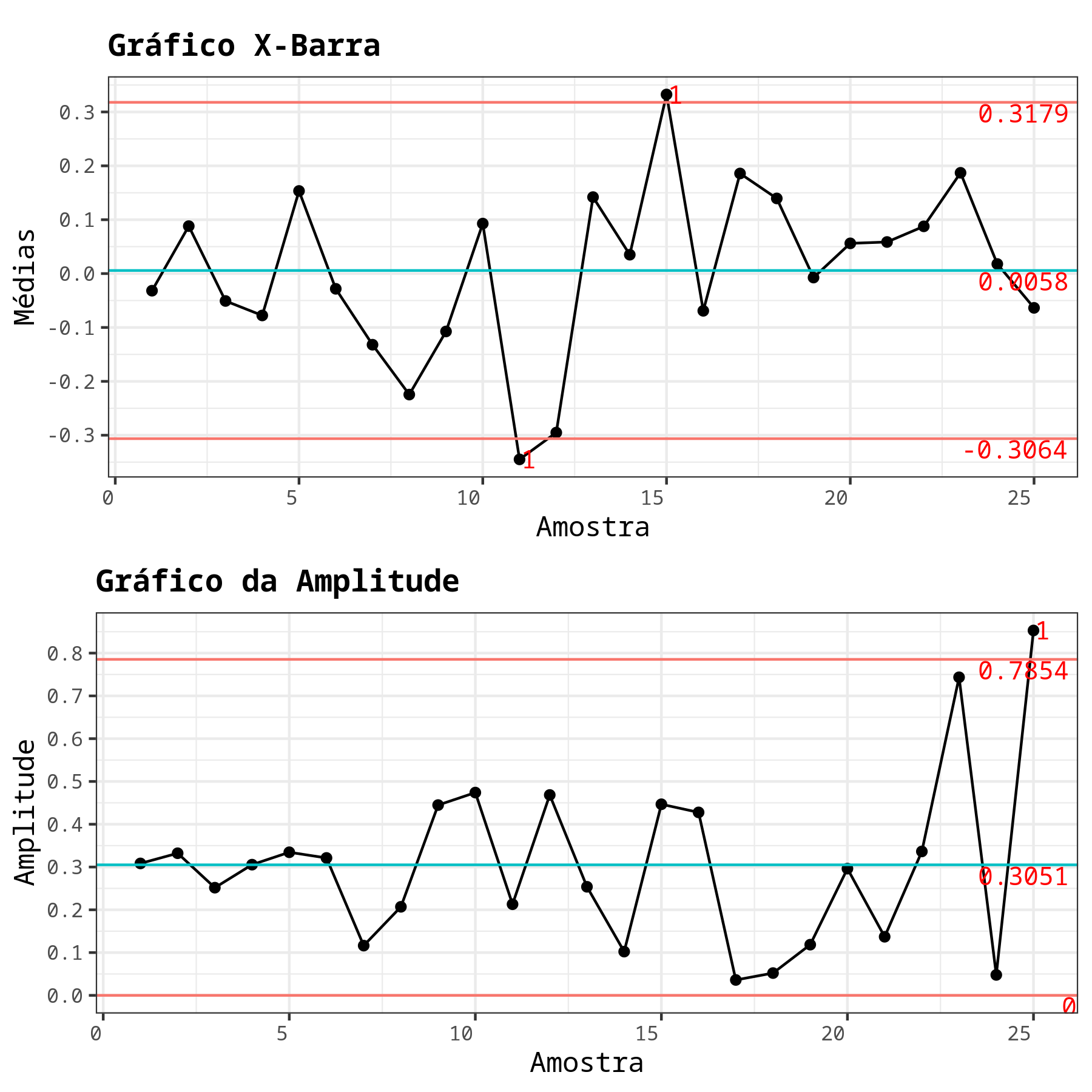
Os resultados são:
Limites - X-barra
| Limites | |
|---|---|
| Limite Superior | 0.318 |
| Linha de centro | 0.006 |
| Limite Inferior | -0.306 |
Limites - R
| Limites | |
|---|---|
| Desvio Padrão | 0.180 |
| Limite Superior | 0.785 |
| Linha de centro | 0.305 |
| Limite Inferior | 0.000 |
Exemplo 2:
Na usinagem bruta de diâmetros externos (eixos) em torno mecânico foram retiradas 25 amostras, cada uma constituída de 3 peças, obtendo-se os valores da tabela abaixo.
| Amostra | N | Peca | P1 | P2 | P3 |
|---|---|---|---|---|---|
| 1 | 220 | 1 | 219.7838 | 220.0287 | 220.0922 |
| 2 | 220 | 1 | 219.9046 | 220.1229 | 220.2368 |
| 3 | 220 | 1 | 219.8345 | 220.0862 | 219.9268 |
| 4 | 220 | 1 | 219.7302 | 220.001 | 220.0357 |
| 5 | 220 | 1 | 220.1644 | 220.3151 | 219.9806 |
| 6 | 260 | 2 | 259.8635 | 260.1847 | 259.867 |
| 7 | 260 | 2 | 259.7917 | 259.9042 | 259.908 |
| 8 | 260 | 2 | 259.8264 | 259.8535 | 259.6465 |
| 9 | 260 | 2 | 259.6421 | 260.0869 | 259.9488 |
| 10 | 260 | 2 | 259.8945 | 260.0154 | 260.3685 |
| 11 | 320 | 3 | 319.7366 | 319.5236 | 319.7053 |
| 12 | 320 | 3 | 319.8834 | 319.415 | 319.8163 |
| 13 | 320 | 3 | 320.2431 | 320.1935 | 319.9893 |
| 14 | 320 | 3 | 319.9805 | 320.0828 | 320.0418 |
| 15 | 320 | 3 | 320.4944 | 320.4552 | 320.0477 |
| 16 | 240 | 4 | 239.8076 | 239.7787 | 240.2064 |
| 17 | 240 | 4 | 240.1663 | 240.1888 | 240.2023 |
| 18 | 240 | 4 | 240.1662 | 240.1382 | 240.1141 |
| 19 | 240 | 4 | 240.017 | 239.9212 | 240.0397 |
| 20 | 240 | 4 | 240.2081 | 240.0484 | 239.9119 |
| 21 | 300 | 5 | 300.0479 | 300.1325 | 299.9955 |
| 22 | 300 | 5 | 300.2815 | 299.9451 | 300.0365 |
| 23 | 300 | 5 | 299.7173 | 300.383 | 300.4608 |
| 24 | 300 | 5 | 300.0009 | 300.0487 | 300.0038 |
| 25 | 300 | 5 | 299.5822 | 300.4351 | 299.7919 |

Realizaremos a análise configurando conforme a figura de abaixo.
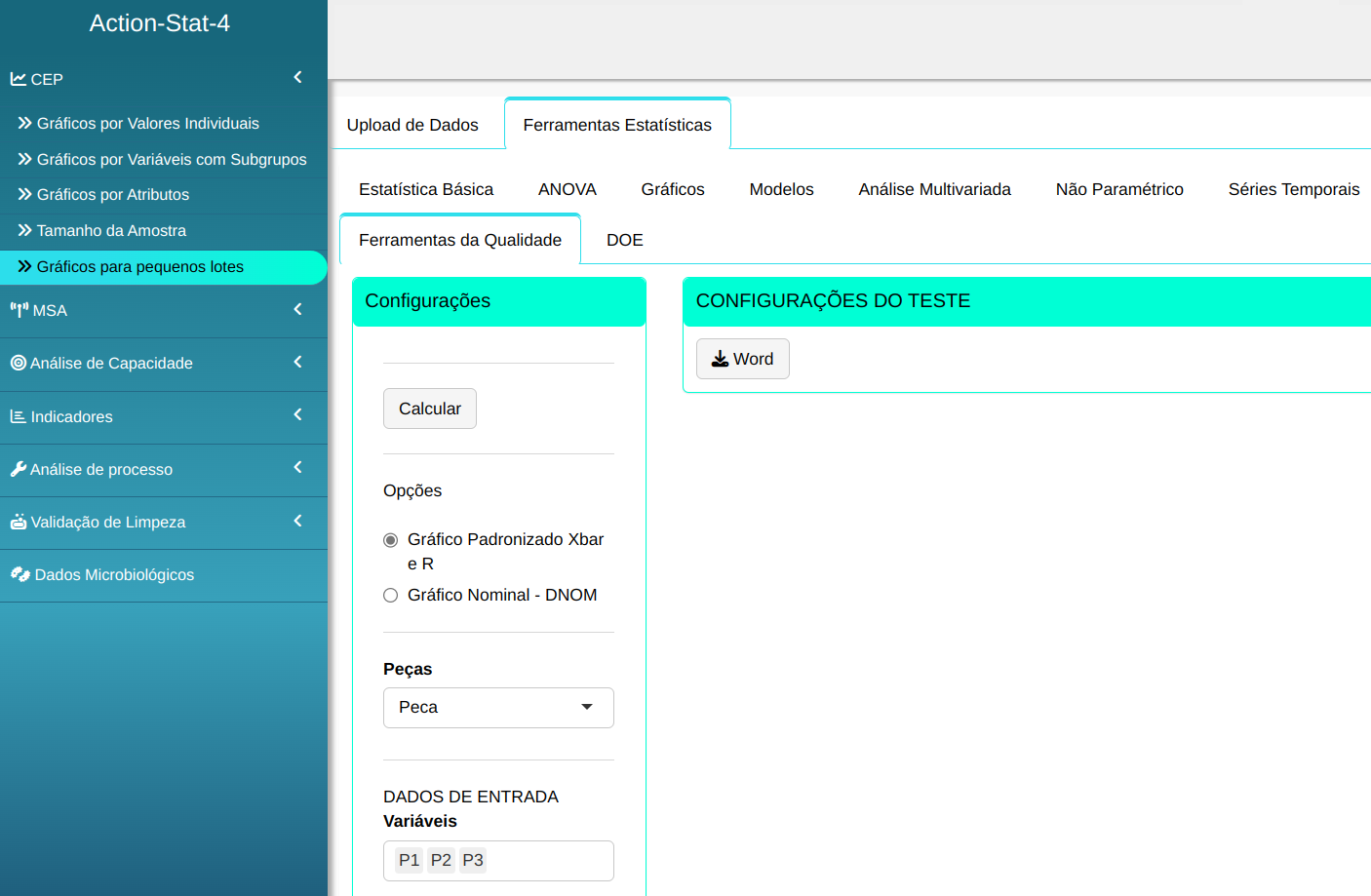

Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e baixar em formato Word.

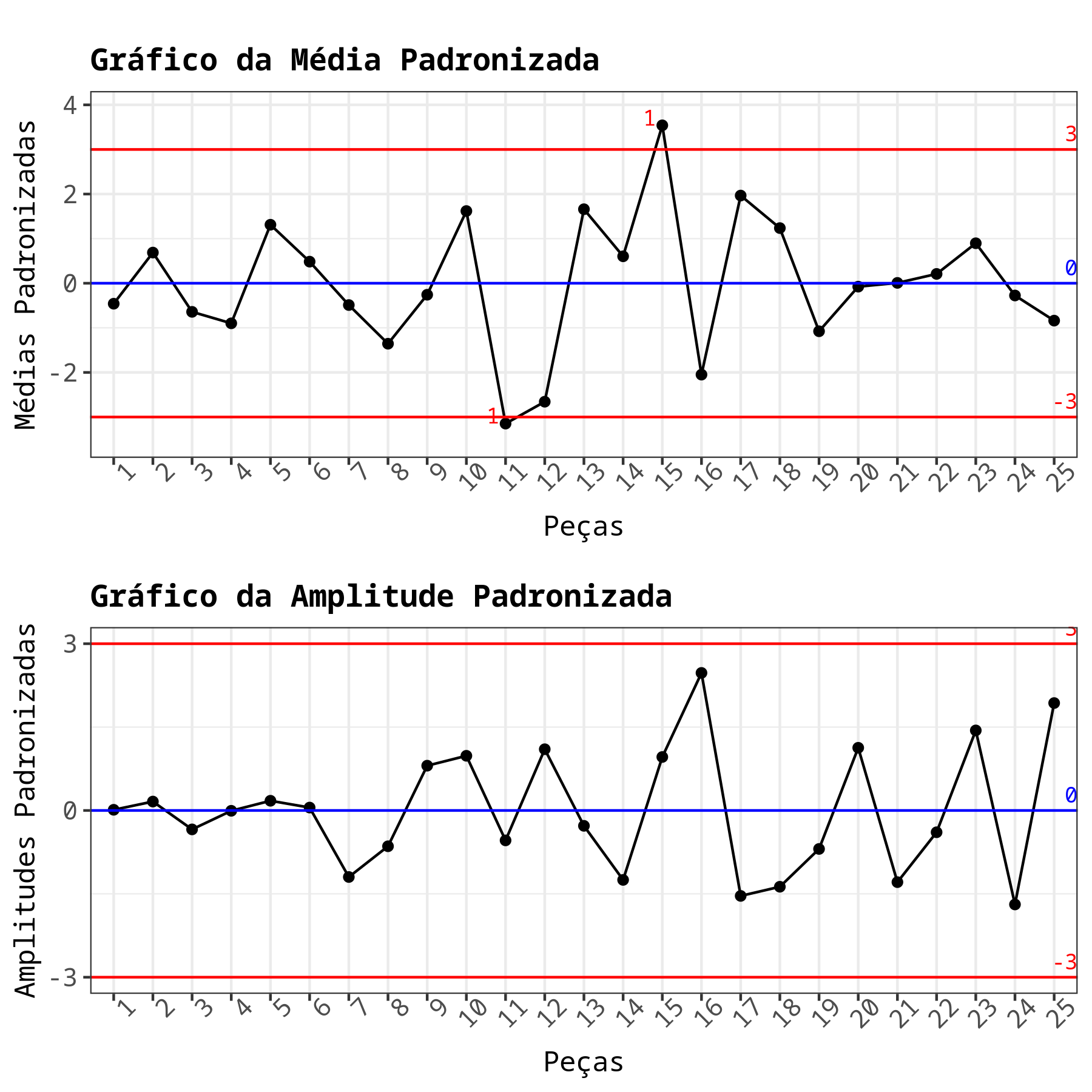
Os resultados são:
Estimativas por peça
| Peças | Médias Padronizadas | Amplitudes Padronizadas | Estimativa do desvio-padrão |
|---|---|---|---|
| 1 | 220.016 | 0.306 | 0.181 |
| 2 | 259.920 | 0.313 | 0.185 |
| 3 | 319.974 | 0.297 | 0.175 |
| 4 | 240.061 | 0.186 | 0.110 |
| 5 | 300.058 | 0.424 | 0.250 |
Padronização por amostra
| Peças | Médias Padronizadas | Amplitudes Padronizadas | |
|---|---|---|---|
| 1 | 1 | -0.459 | 0.012 |
| 2 | 1 | 0.687 | 0.16 |
| 3 | 1 | -0.642 | -0.341 |
| 4 | 1 | -0.899 | -0.006 |
| 5 | 1 | 1.312 | 0.174 |
| 6 | 2 | 0.484 | 0.052 |
| 7 | 2 | -0.489 | -1.197 |
| 8 | 2 | -1.356 | -0.644 |
| 9 | 2 | -0.258 | 0.806 |
| 10 | 2 | 1.619 | 0.984 |
| 11 | 3 | -3.148 | -0.538 |
| 12 | 3 | -2.657 | 1.102 |
| 13 | 3 | 1.66 | -0.276 |
| 14 | 3 | 0.604 | -1.249 |
| 15 | 3 | 3.541 | 0.962 |
| 16 | 4 | -2.049 | 2.474 |
| 17 | 4 | 1.966 | -1.537 |
| 18 | 4 | 1.237 | -1.372 |
| 19 | 4 | -1.077 | -0.692 |
| 20 | 4 | -0.077 | 1.128 |
| 21 | 5 | 0.008 | -1.289 |
| 22 | 5 | 0.209 | -0.392 |
| 23 | 5 | 0.897 | 1.44 |
| 24 | 5 | -0.275 | -1.691 |
| 25 | 5 | -0.838 | 1.932 |