4. Tendência e Linearidade
Linearidade é medida pelo declive da linha formada pelos diferentes valores de referência em relação a sua tendência. Quanto menos inclinada for a linha, melhor a qualidade dos sistemas de medição.
Exemplo 1:
Como aplicação de um estudo de tendência e linearidade, vamos avaliar um sistema de medição para medir a temperatura de um forno via um pirômetro óptico. Para isto, vamos fazer um estudo por comparação com um termo elemento padrão. Tomamos 5 níveis de temperatura:
| Padrão | Medidas | VR | Tolerância |
|---|---|---|---|
| 1 | 748,8 | 750 | 100 |
| 1 | 749,8 | 750 | 100 |
| 1 | 748,8 | 750 | 100 |
| 1 | 748,8 | 750 | 100 |
| 1 | 748,8 | 750 | 100 |
| 1 | 748,8 | 750 | 100 |
| 1 | 747,7 | 750 | 100 |
| 1 | 747,7 | 750 | 100 |
| 1 | 747,7 | 750 | 100 |
| 1 | 748,7 | 750 | 100 |
| 1 | 749,7 | 750 | 100 |
| 1 | 750,7 | 750 | 100 |
| 2 | 848,8 | 850 | 100 |
| 2 | 848,8 | 850 | 100 |
| 2 | 848,8 | 850 | 100 |
| 2 | 847,2 | 850 | 100 |
| 2 | 847,2 | 850 | 100 |
| 2 | 847,2 | 850 | 100 |
| 2 | 846,1 | 850 | 100 |
| 2 | 846,1 | 850 | 100 |
| 2 | 846,2 | 850 | 100 |
| 2 | 846,3 | 850 | 100 |
| 2 | 847,3 | 850 | 100 |
| 2 | 848,3 | 850 | 100 |
| 3 | 946,9 | 950 | 100 |
| 3 | 946,9 | 950 | 100 |
| 3 | 946,9 | 950 | 100 |
| 3 | 945,8 | 950 | 100 |
| 3 | 944,8 | 950 | 100 |
| 3 | 944,8 | 950 | 100 |
| 3 | 943,6 | 950 | 100 |
| 3 | 943,6 | 950 | 100 |
| 3 | 943,6 | 950 | 100 |
| 3 | 945,1 | 950 | 100 |
| 3 | 946,1 | 950 | 100 |
| 3 | 947,1 | 950 | 100 |
| 4 | 1045,4 | 1050 | 100 |
| 4 | 1045,4 | 1050 | 100 |
| 4 | 1045,4 | 1050 | 100 |
| 4 | 1044,9 | 1050 | 100 |
| 4 | 1043,9 | 1050 | 100 |
| 4 | 1044,9 | 1050 | 100 |
| 4 | 1042 | 1050 | 100 |
| 4 | 1042 | 1050 | 100 |
| 4 | 1042 | 1050 | 100 |
| 4 | 1045,6 | 1050 | 100 |
| 4 | 1046,6 | 1050 | 100 |
| 4 | 1047,6 | 1050 | 100 |
| 5 | 1141,9 | 1150 | 100 |
| 5 | 1141,3 | 1150 | 100 |
| 5 | 1142,9 | 1150 | 100 |
| 5 | 1144,3 | 1150 | 100 |
| 5 | 1143,5 | 1150 | 100 |
| 5 | 1140,9 | 1150 | 100 |
| 5 | 1141,9 | 1150 | 100 |
| 5 | 1142,2 | 1150 | 100 |
| 5 | 1142,1 | 1150 | 100 |
| 5 | 1140 | 1150 | 100 |
| 5 | 1140,7 | 1150 | 100 |
| 5 | 1142,7 | 1150 | 100 |
Faremos o upload dos dados no sistema.
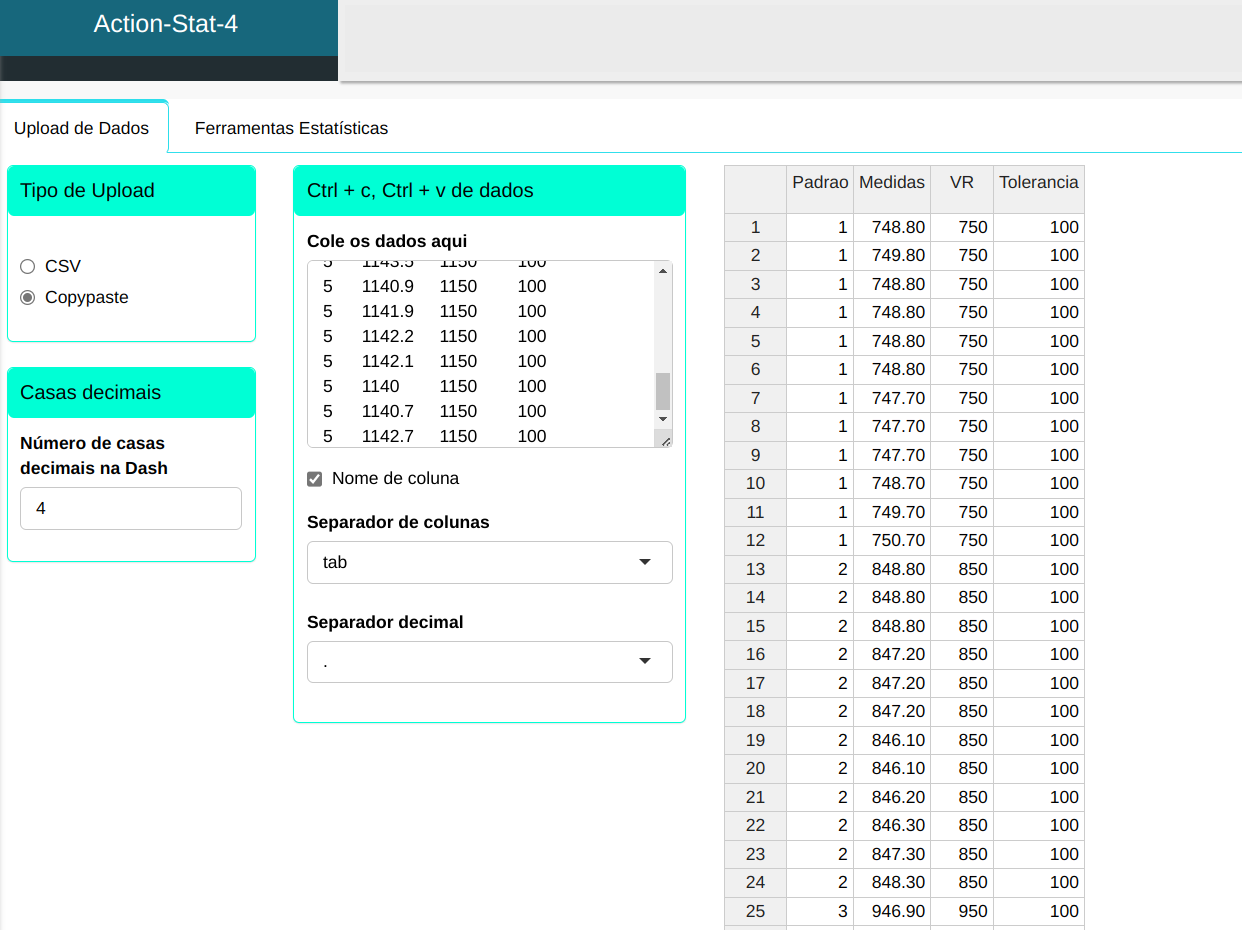
Realizaremos a análise configurando conforme a figura abaixo.
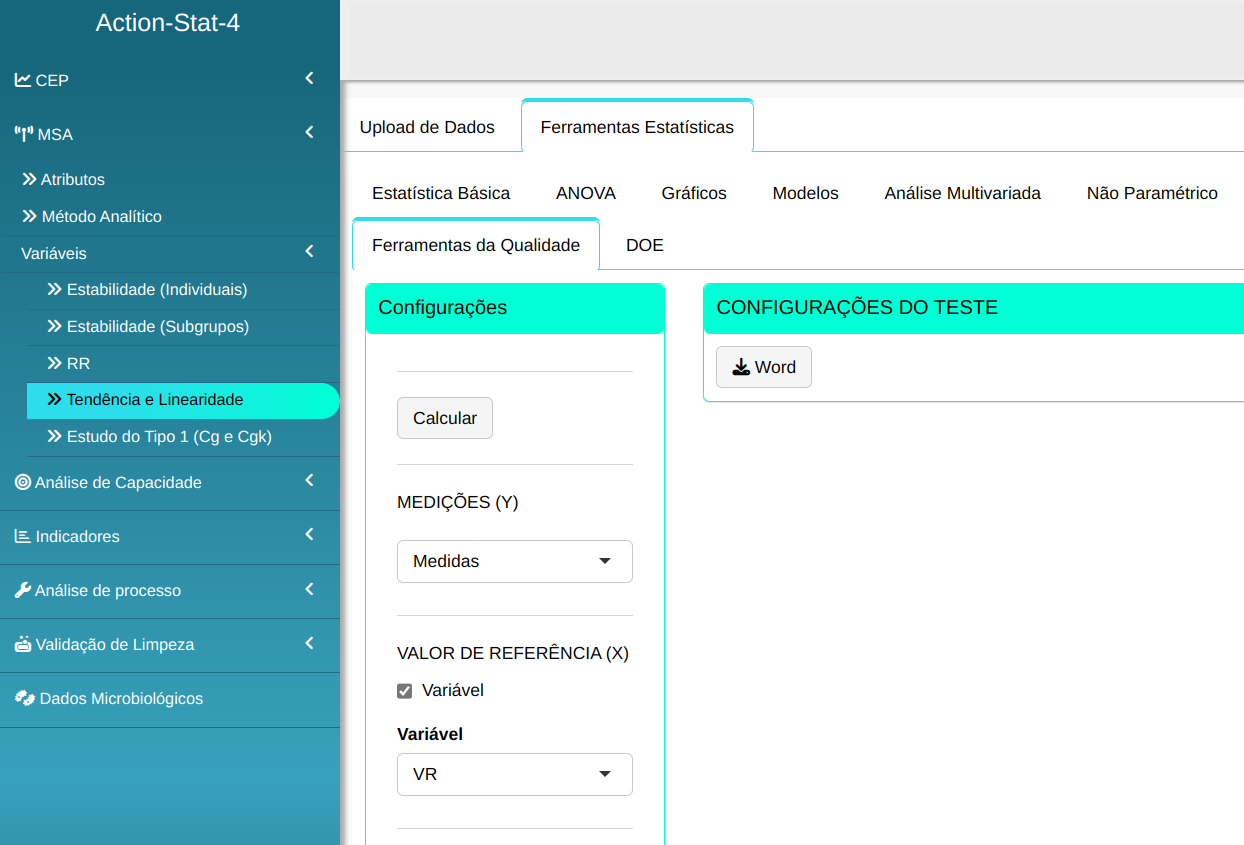
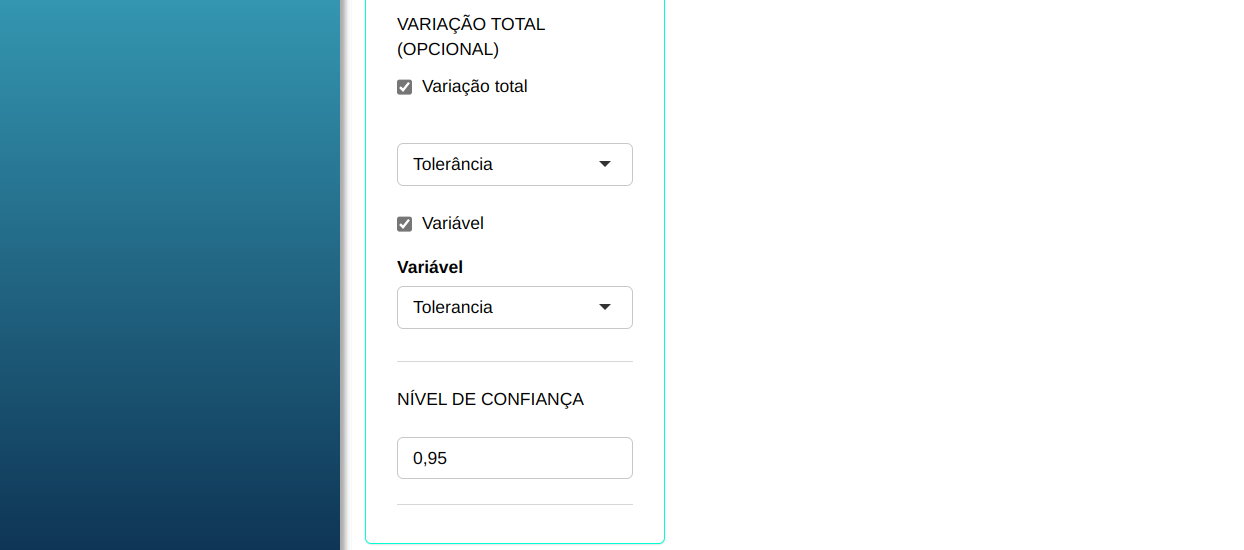
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e baixar em formato Word.

Os resultados são:
Resultado da análise
| ANÁLISE DE LINEARIDADE |
Testes dos Coeficientes da Regressão linear
| Estimativa | Desvio padrão | Estatística t | P-valor | |
|---|---|---|---|---|
| (Intercepto) | 11.161 | 1.167 | 9.567 | 0 |
| Coeficiente angular | -0.016 | 0.001 | -13.433 | 0 |
Medida Descritiva da Qualidade do Ajuste
| R^2 | R^2 Ajustado | Estatística t |
|---|---|---|
| 0.757 | 0.753 | 180.456 |
Resultado da análise
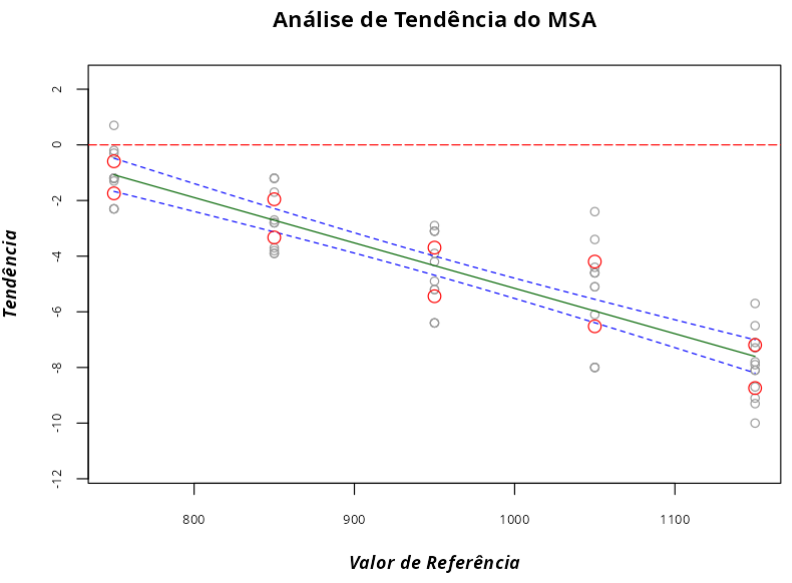
| Análise de Tendência do MSA |
ANÁLISE DE TENDÊNCIA - Teste t
| Valor de Referência | Média | Tendência | Estatística t | P-valor | Limite Inferior | Limite Superior | VE % | Desvio-padrão |
|---|---|---|---|---|---|---|---|---|
| 750 | 748.833 | -1.167 | -4.456 | 0.001 | -1.743 | -0.590 | 5.441 | 0.907 |
| 850 | 847.358 | -2.642 | -8.474 | 0.000 | -3.328 | -1.956 | 6.480 | 1.080 |
| 950 | 945.433 | -4.567 | -11.502 | 0.000 | -5.441 | -3.693 | 8.252 | 1.375 |
| 1050 | 1044.642 | -5.358 | -10.142 | 0.000 | -6.521 | -4.195 | 10.982 | 1.830 |
| 1150 | 1142.033 | -7.967 | -22.680 | 0.000 | -8.740 | -7.194 | 7.301 | 1.217 |
Resultado da Análise
| Média das tendências | ||
| $\quad \qquad$-4.34 |
Exemplo 2:
O engenheiro do sistema de medição estava interessado em determinar a linearidade de um sistema de medição. Cinco peças padrão, que se distribuem por toda a faixa de variação do processo, foram medidas 15 vezes no laboratório de medição para se determinar o valor de referência. Neste caso, o metrologista utilizou um instrumento de medição com uma resolução melhor do que o instrumento utilizado normalmente. Após determinar o valor de referência, um avaliador realizou 12 medições de cada peça padrão. Os valores estão resumidos na Tabela abaixo. Aqui,temos g=5 (número de peças) e m=12 (leituras em cada peça).
| Peças | Medições | VR | Histórico |
|---|---|---|---|
| 1 | 2,7 | 2 | 0,744067 |
| 2 | 2,5 | 2 | 0,744067 |
| 3 | 2,4 | 2 | 0,744067 |
| 4 | 2,5 | 2 | 0,744067 |
| 5 | 2,7 | 2 | 0,744067 |
| 6 | 2,3 | 2 | 0,744067 |
| 7 | 2,5 | 2 | 0,744067 |
| 8 | 2,5 | 2 | 0,744067 |
| 9 | 2,4 | 2 | 0,744067 |
| 10 | 2,4 | 2 | 0,744067 |
| 11 | 2,6 | 2 | 0,744067 |
| 12 | 2,4 | 2 | 0,744067 |
| 1 | 5,1 | 4 | 2,684806 |
| 2 | 3,9 | 4 | 2,684806 |
| 3 | 4,2 | 4 | 2,684806 |
| 4 | 5 | 4 | 2,684806 |
| 5 | 3,8 | 4 | 2,684806 |
| 6 | 3,9 | 4 | 2,684806 |
| 7 | 3,9 | 4 | 2,684806 |
| 8 | 3,9 | 4 | 2,684806 |
| 9 | 3,9 | 4 | 2,684806 |
| 10 | 4 | 4 | 2,684806 |
| 11 | 4,1 | 4 | 2,684806 |
| 12 | 3,8 | 4 | 2,684806 |
| 1 | 5,8 | 6 | 1,175894 |
| 2 | 5,7 | 6 | 1,175894 |
| 3 | 5,9 | 6 | 1,175894 |
| 4 | 5,9 | 6 | 1,175894 |
| 5 | 6 | 6 | 1,175894 |
| 6 | 6,1 | 6 | 1,175894 |
| 7 | 6 | 6 | 1,175894 |
| 8 | 6,1 | 6 | 1,175894 |
| 9 | 6,4 | 6 | 1,175894 |
| 10 | 6,3 | 6 | 1,175894 |
| 11 | 6 | 6 | 1,175894 |
| 12 | 6,1 | 6 | 1,175894 |
| 1 | 7,6 | 8 | 0,597723 |
| 2 | 7,7 | 8 | 0,597723 |
| 3 | 7,8 | 8 | 0,597723 |
| 4 | 7,7 | 8 | 0,597723 |
| 5 | 7,8 | 8 | 0,597723 |
| 6 | 7,8 | 8 | 0,597723 |
| 7 | 7,8 | 8 | 0,597723 |
| 8 | 7,7 | 8 | 0,597723 |
| 9 | 7,8 | 8 | 0,597723 |
| 10 | 7,5 | 8 | 0,597723 |
| 11 | 7,6 | 8 | 0,597723 |
| 12 | 7,7 | 8 | 0,597723 |
| 1 | 9,1 | 10 | 0,880083 |
| 2 | 9,3 | 10 | 0,880083 |
| 3 | 9,5 | 10 | 0,880083 |
| 4 | 9,3 | 10 | 0,880083 |
| 5 | 9,4 | 10 | 0,880083 |
| 6 | 9,5 | 10 | 0,880083 |
| 7 | 9,5 | 10 | 0,880083 |
| 8 | 9,5 | 10 | 0,880083 |
| 9 | 9,6 | 10 | 0,880083 |
| 10 | 9,2 | 10 | 0,880083 |
| 11 | 9,3 | 10 | 0,880083 |
| 12 | 9,4 | 10 | 0,880083 |
Faremos o upload dos dados no sistema.
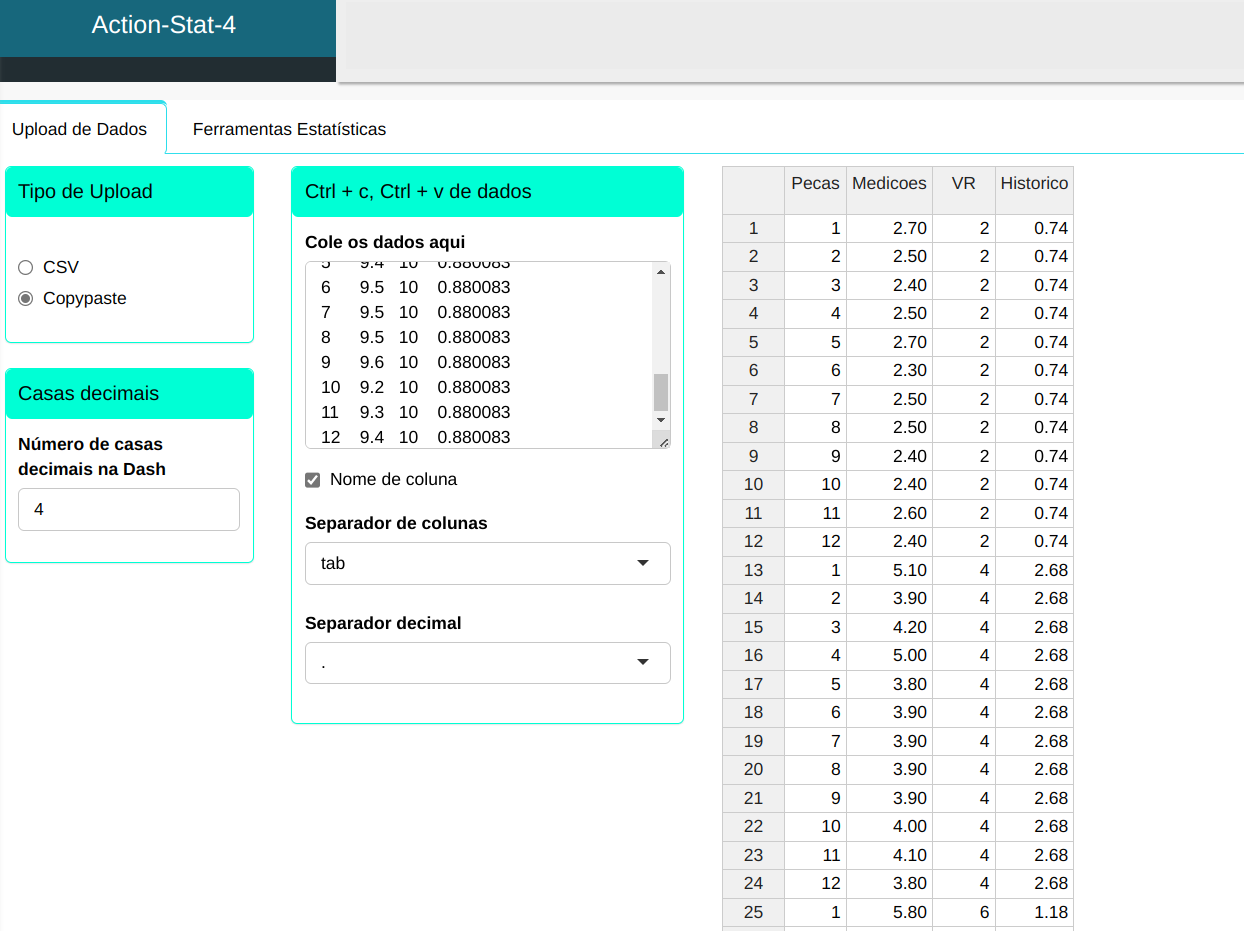
Faremos a análise configurando conforme a figura abaixo.
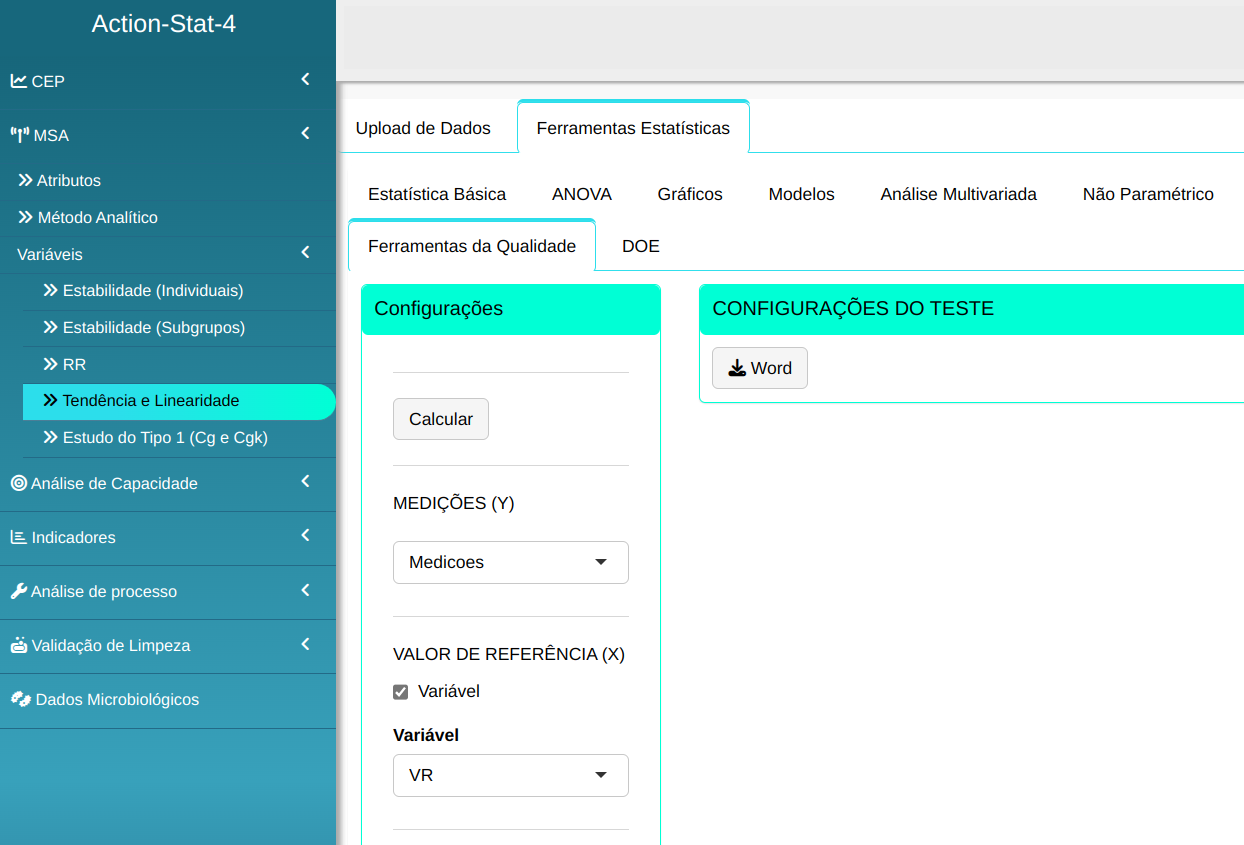
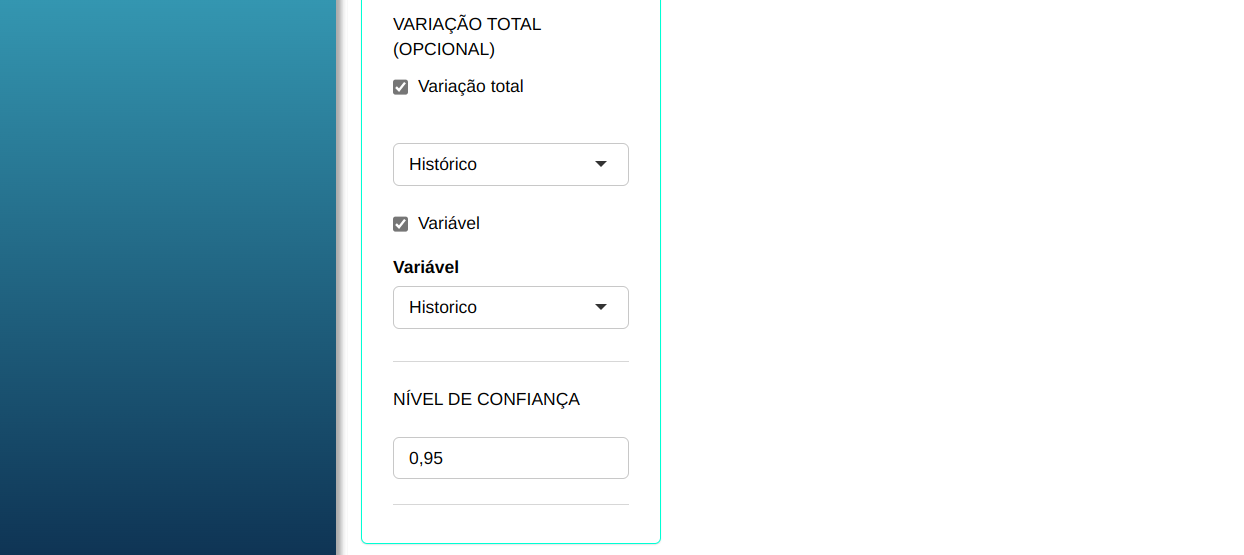
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e baixar em formato Word.

Os resultados são:
| ANÁLISE DE LINEARIDADE |
Testes dos Coeficientes da Regressão linear
| Estimativa | Desvio padrão | Estatística t | P-valor | |
|---|---|---|---|---|
| (Intercepto) | 0.737 | 0.073 | 10.158 | 0 |
| Coeficiente angular | -0.132 | 0.011 | -12.043 | 0 |
Medida Descritiva da Qualidade do Ajuste
| R^2 | R^2 Ajustado | Estatística t |
|---|---|---|
| 0.714 | 0.709 | 145.023 |
Resultado da análise
| Análise de Tendência do MSA |
ANÁLISE DE TENDÊNCIA - Teste t
| Valor de Referência | Média | Tendência | Estatística t | P-valor | Limite Inferior | Limite Superior | VE % | Desvio-padrão |
|---|---|---|---|---|---|---|---|---|
| 2 | 2.492 | 0.492 | 13.734 | 0 | 0.413 | 0.57 | 16.666 | 0.124 |
| 4 | 4.125 | 0.125 | 0.968 | 0.354 | -0.159 | 0.409 | 16.667 | 0.447 |
| 6 | 6.025 | 0.025 | 0.442 | 0.667 | -0.1 | 0.15 | 16.667 | 0.196 |
| 8 | 7.708 | -0.292 | -10.142 | 0 | -0.355 | -0.228 | 16.667 | 0.1 |
| 10 | 9.383 | -0.617 | -14.564 | 0 | -0.71 | -0.523 | 16.666 | 0.147 |
Resultado da Análise
| Média das Tendência | ||
| $\qquad \quad$-0.0533 |
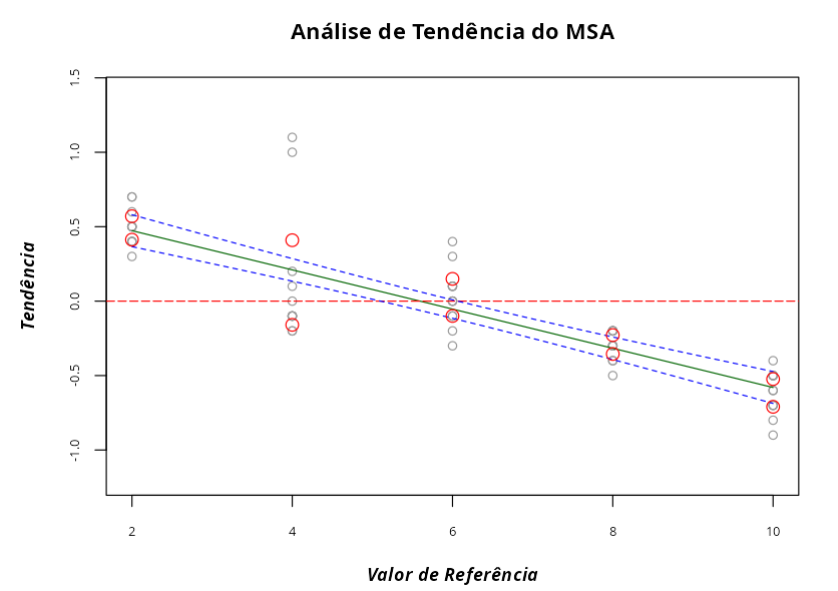
A tendência é considerada significativa ao nível 0,05 para os valores de referência 2,8 e 10, pois o 0 não se encontra entre os limites de confiança.
A linearidade também é considerada significativa ao nível 0,05, pois o p-valor é menor que 0,05, o que também pode ser observado pelo gráfico de Tendência.
Exemplo 3:
Vamos avaliar a tendência de um sistema de medição para medir a altura de um “MP3 Player”. Esta altura é medida com um altímetro. Um “MP3 Player” foi selecionado (próximo ao valor nominal) e seu valor de referência foi estabelecido com um sistema de medição por coordenadas, no qual VR = 89,73 mm, e temos uma tolerância 0,7mm. A seguir, o mesmo “MP3 Player” foi medido 12 vezes com o sistema de medição em análise.
| Amostra | Medidas |
|---|---|
| 1 | 89,77 |
| 2 | 89,79 |
| 3 | 89,77 |
| 4 | 89,78 |
| 5 | 89,74 |
| 6 | 89,72 |
| 7 | 89,72 |
| 8 | 89,75 |
| 9 | 89,74 |
| 10 | 89,77 |
| 11 | 89,78 |
| 12 | 89,74 |
Faremos o upload dos dados no sistema.
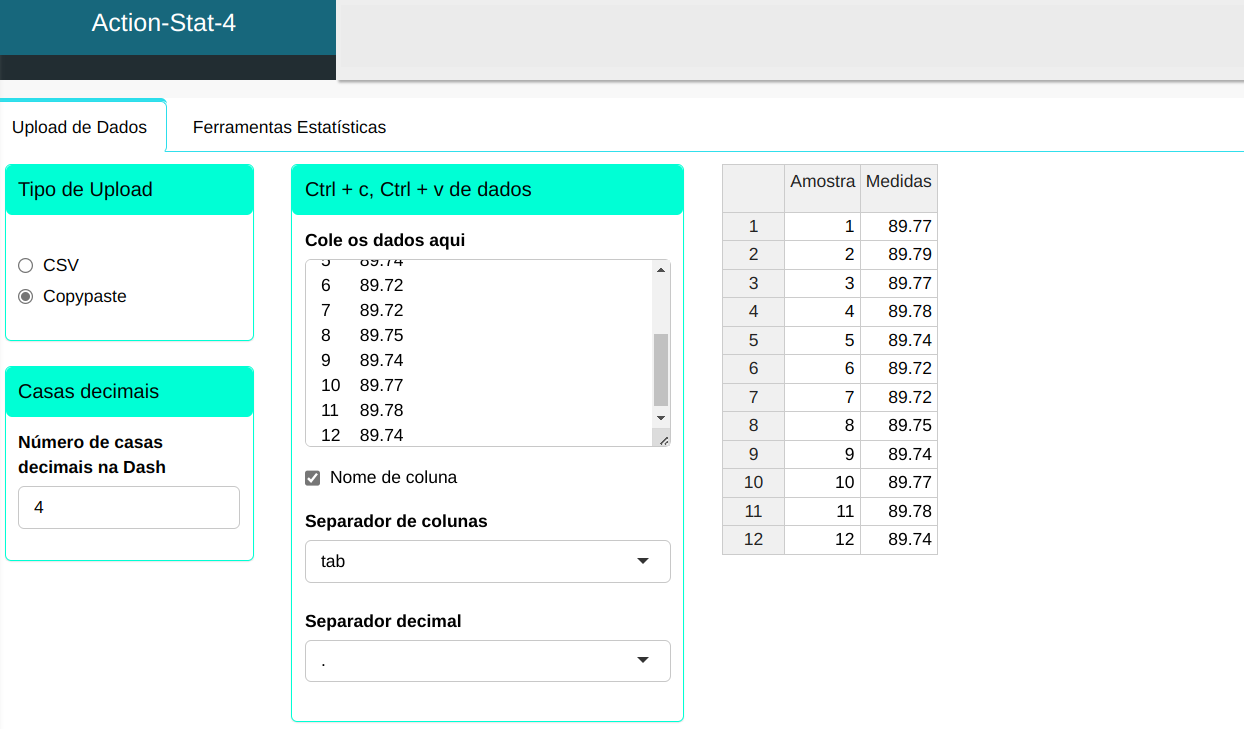
Faremos a análise configurando conforme a figura abaixo.
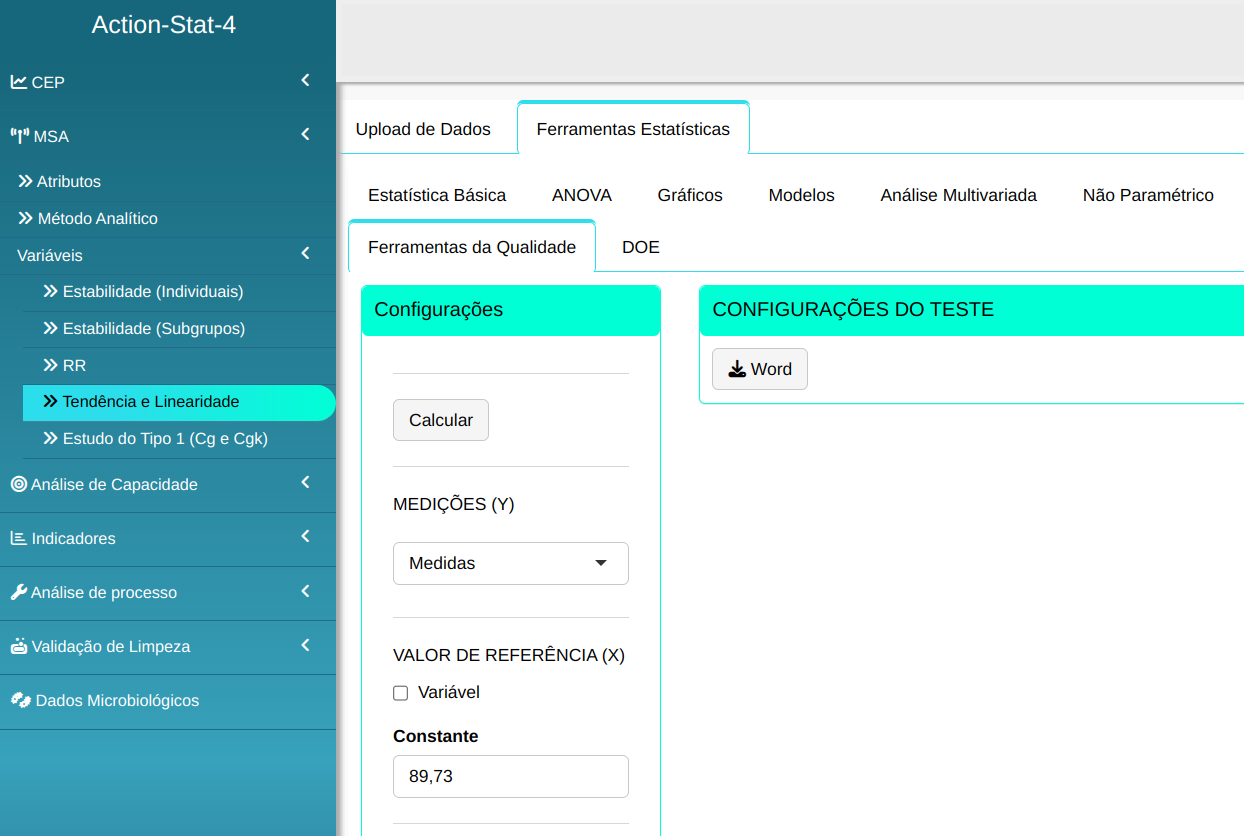
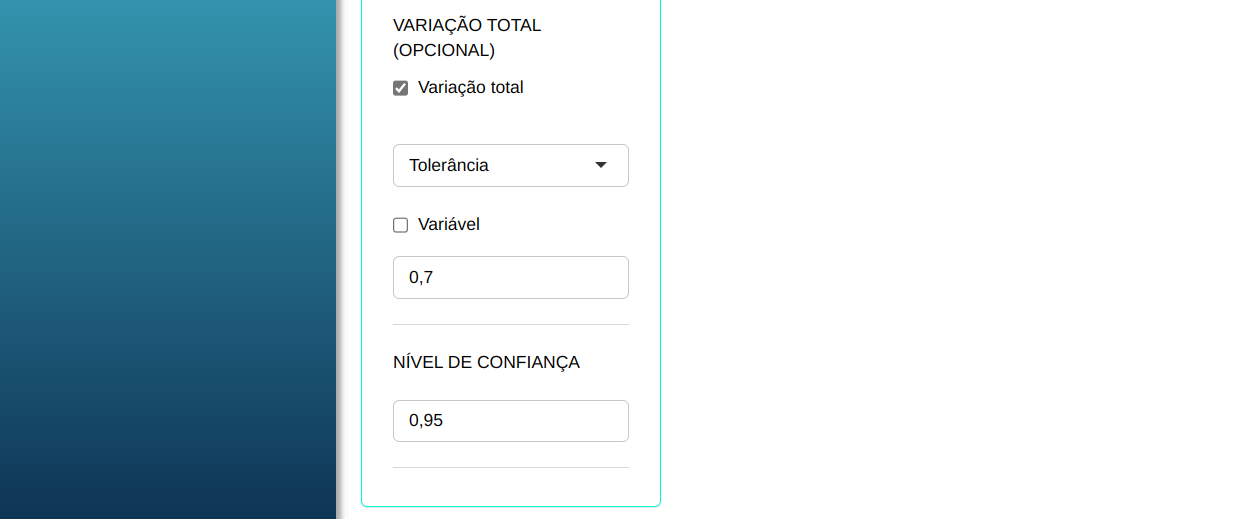
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e baixar em formato Word.

Os resultados são:
ANÁLISE DE TENDÊNCIA - Teste t
| V1 | |
|---|---|
| Valor de Referência | 89.730 |
| Média | 89.756 |
| Tendência | 0.026 |
| Estatística t | 3.742 |
| P-valor | 0.003 |
| Limite Inferior | 0.011 |
| Limite Superior | 0.041 |
| VE % | 20.499 |
| Desvio padrão | 0.024 |
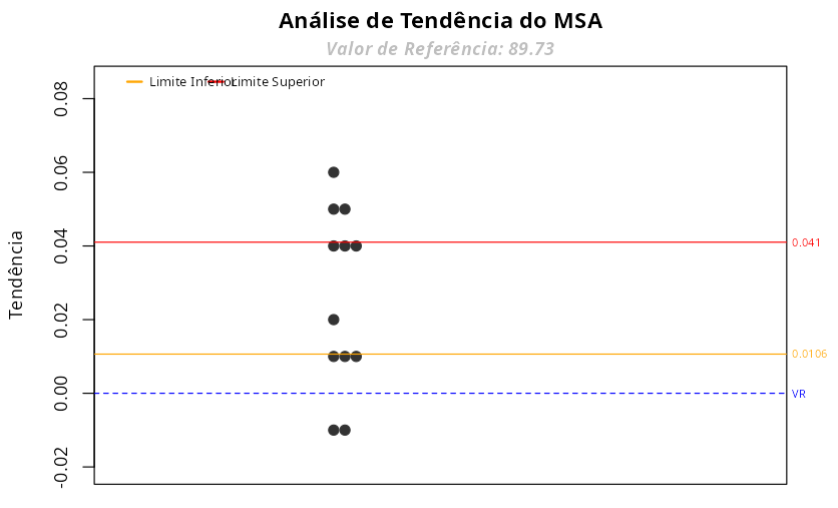
A tendência é considerada significativa ao nível 0,95, pois o 0 não se encontra entre os limites de confiança.
O gráfico de tendência também mostra que muitos pontos têm tendência fora desses limites.
Exemplo 4:
Um engenheiro está avaliando um novo sistema de medição para monitorar um processo. Uma análise do sistema de medição indicou que não deve haver preocupação com a linearidade, pois a faixa de interesse é pequena. Uma única peça foi escolhida de tal forma que esteja próxima ao valor nominal dos processos. A peça foi medida por um sistema de medição sofisticado para determinar seu valor de referência (valor de referência = 6). A peça foi então medida 15 vezes por um operador e o valor da variabilidade total do processo é de 2,5, este valor será utilizado para validar a repetitividade do sistema de medição.
| Ensaios | Medidas |
|---|---|
| 1 | 5,8 |
| 2 | 5,7 |
| 3 | 5,9 |
| 4 | 5,9 |
| 5 | 6,0 |
| 6 | 6,1 |
| 7 | 6,0 |
| 8 | 6,1 |
| 9 | 6,4 |
| 10 | 6,3 |
| 11 | 6,0 |
| 12 | 6,1 |
| 13 | 6,2 |
| 14 | 5,6 |
| 15 | 6,0 |
Faremos o upload dos dados no sistema.
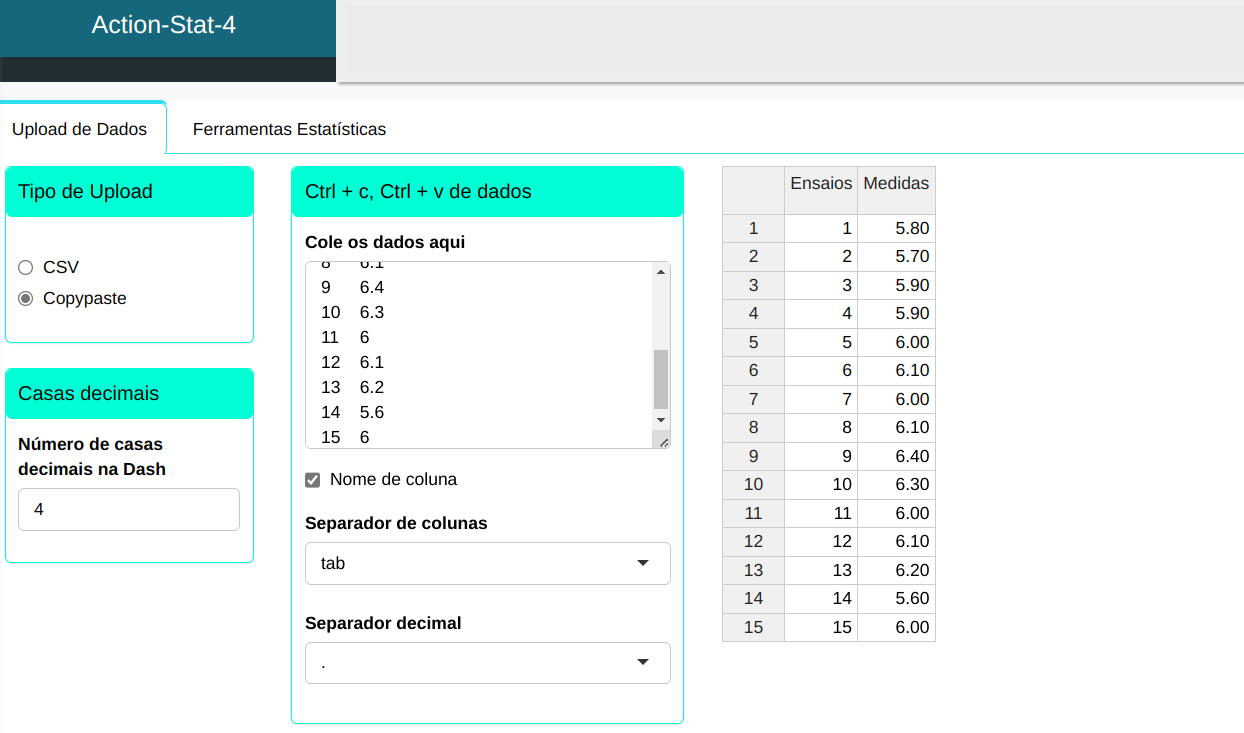
Realizaremos a análise configurando conforme a figura abaixo.
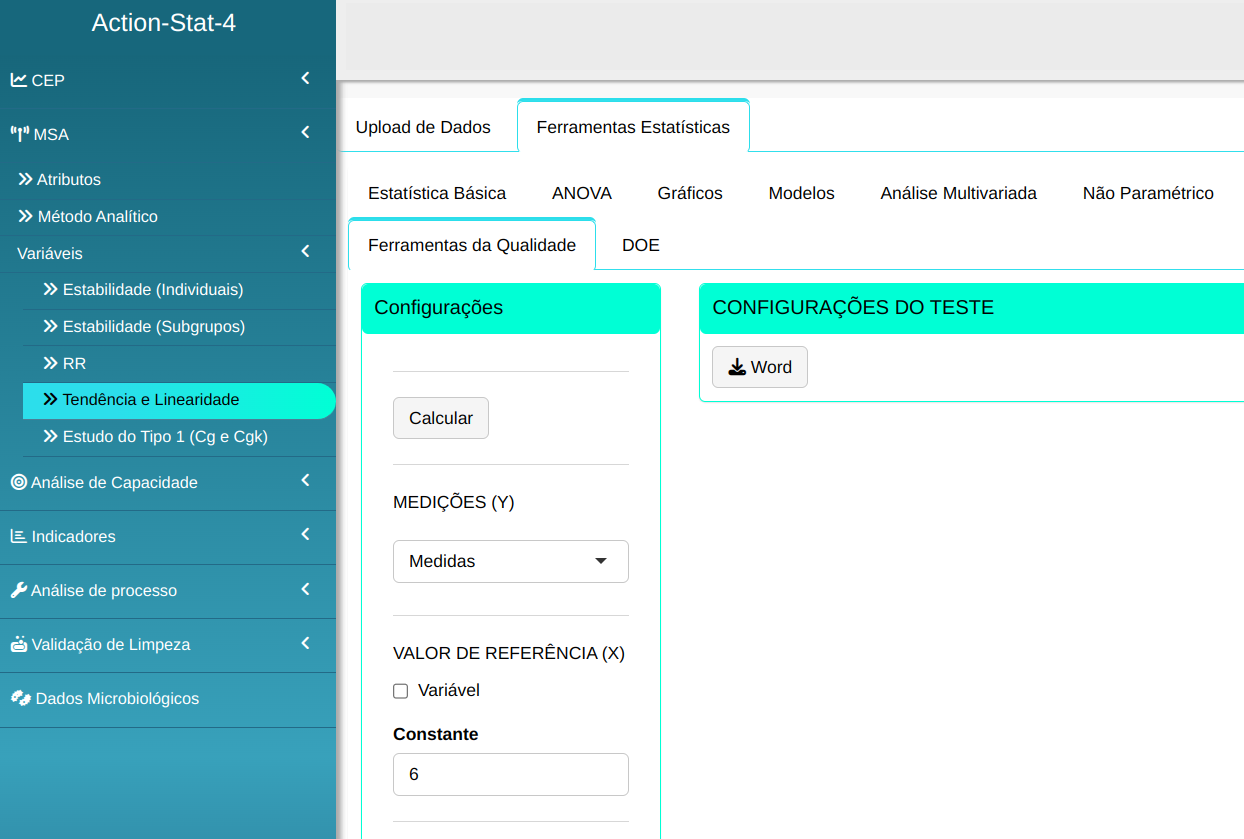
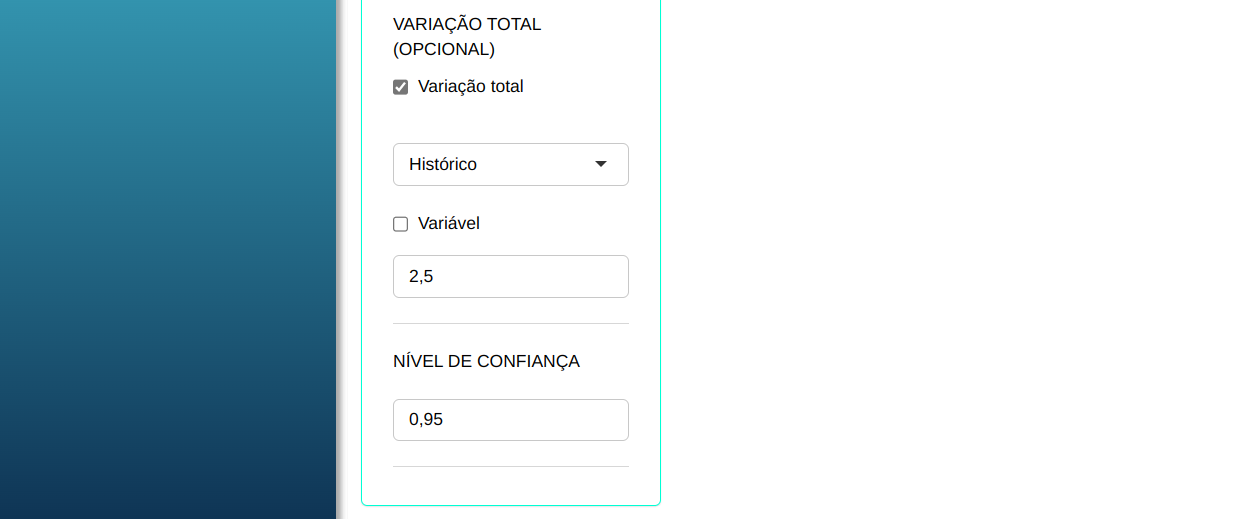
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e baixar em formato Word.

Os resultados são:
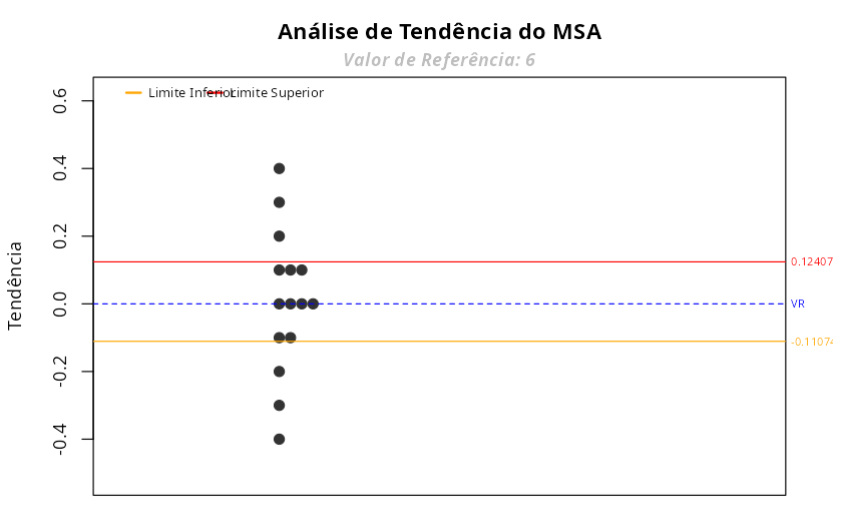
ANÁLISE DE TENDÊNCIA - Teste t
| V1 | |
|---|---|
| Valor de Referência | 6 |
| Média | 6.007 |
| Tendência | 0.007 |
| Estatística t | 0.122 |
| P-valor | 0.905 |
| Limite Inferior | -0.111 |
| Limite Superior | 0.124 |
| VE % | 8.481 |
| Desvio padrão | 0.212 |