5. Histograma

Histograma é uma representação gráfica (um gráfico de barras verticais) da distribuição de frequências de um conjunto de dados quantitativos contínuos.

Exemplo:

Em uma fábrica de auto peças, uma arruela de vedação estava causando inconveniente na montagem de uma parte de um automóvel. Para buscar informações, decidimos medir a espessura de 200 arruelas, cujos valores foram:

Espessura de 200 arruelas
8
10
12
12
11,5
8
11,5
9,5
9,5
10,5
13
13,5
11
14,5
12
13
11
10,5
9,5
11,5
12,5
10,5
10,5
12,5
9
13
11,5
14,5
13,5
12,5
10
10,5
8
13
7
8
7
7
9,5
11,5
12,5
8
13,5
15,5
9,5
15
10
10
9
14,5
11
10,5
11,5
8,5
8
10
7,5
10
12,5
8
14
15
11,5
13,5
11,5
9,5
12,5
5
8
13
8,5
7,5
10
11
13,5
9
15,5
12,5
7
10,5
13,5
9
12
12,5
12,5
12,5
9
13,5
12,5
12,5
10,5
8
8,5
13,5
13
13
13
9,5
9,5
14,5
12
13
15,5
17
14
15
13
7,5
12
12
7
12,5
10,5
8,5
6
15
15,5
10
12
8,5
14
11
14
8
11,5
13,5
11,5
11
9,5
13
10
10,5
12
11
10
10
11,5
10
10
10
12
10
7,5
11
13
12
16
9
10
8,5
12
14,5
10,5
11
10
13,5
10,5
12
10
12,5
10
14
11,5
11,5
13
11
10,5
10,5
7,5
10,5
12
12
11
10
12
11,5
9,5
8,5
8,5
12,5
14,5
11
11
17
15
11
9
14
10,5
10,5
10,5
8
10,5
12,5
14,5
7,5
9,5
10
12
11

Faremos o upload dos dados do sistema.

Faremos o Histograma.

Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:

Tabela de Frequências

Classe	Frequência	Freq.Rel.	Freq. Perc.	Freq. Acum.	Densidades	Ponto Médio
[5; 6.2)	2	0.01	1.0	1.0	0.008	5.6
[6.2; 7.4)	5	0.02	2.5	3.5	0.021	6.8
[7.4; 8.6)	25	0.12	12.5	16.0	0.104	8.0
[8.6; 9.8)	18	0.09	9.0	25.0	0.075	9.2
[9.8; 11)	40	0.20	20.0	45.0	0.167	10.4
[11; 12,2)	46	0.23	23.0	68.0	0.192	11.6
[12.2; 13.4)	29	0.14	14.5	82.5	0.121	12.8
[13.4; 14.6)	23	0.12	11.5	94.0	0.096	14.0
[14.6; 15.8)	9	0.04	4.5	98.5	0.038	15.2
[15.8; 17)	3	0.02	1.5	100.0	0.012	16.4

Resumo Descritivo

	Valores
Mínimo	5.000
1º Quartil	9.625
Mediana	11.000
Média	11.152
3º Quartil	12.500
Máximo	17.000
Desvio Padrão	2.249

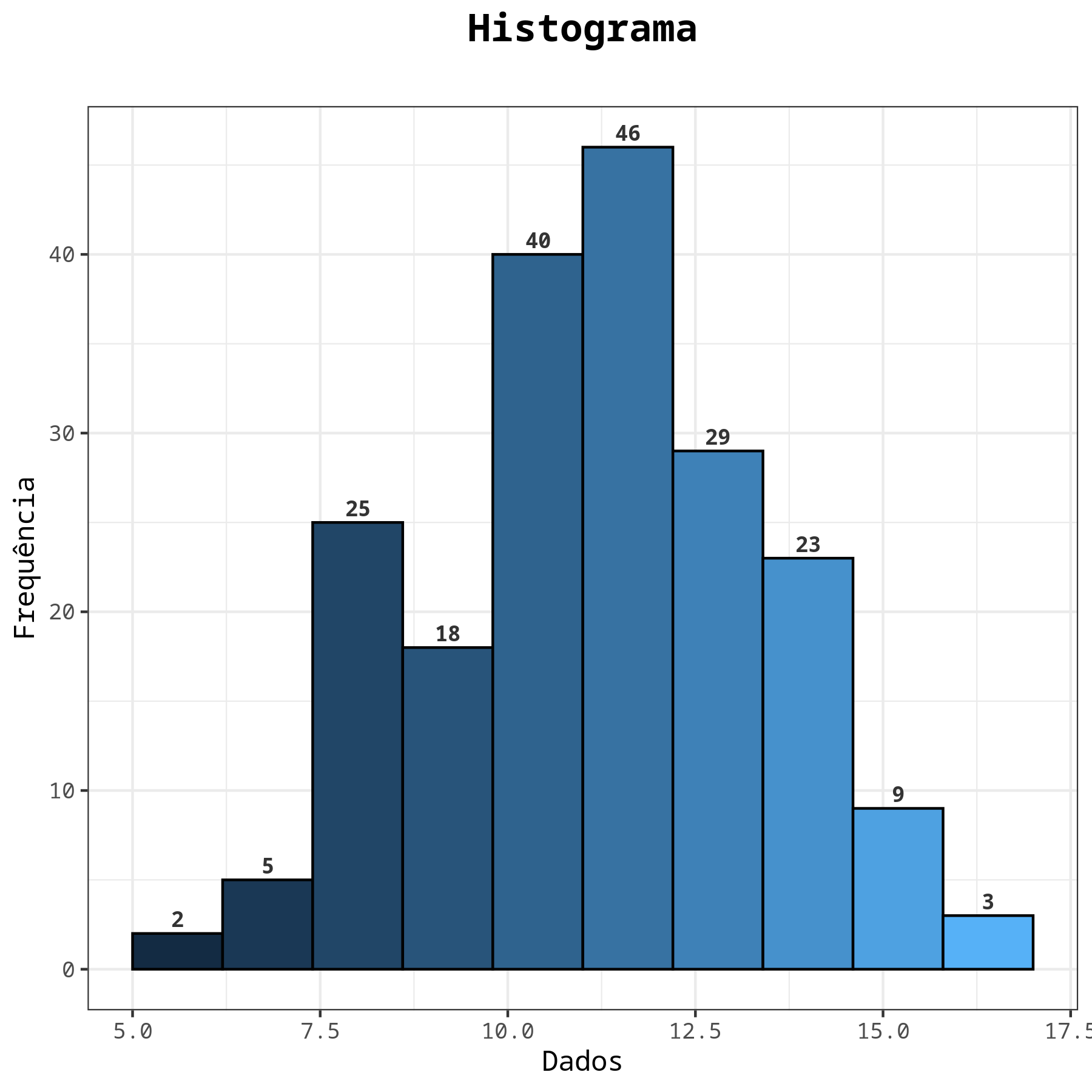
Pelo histograma vemos que as espessuras das arruela seguem, aproximadamente, uma distribuição normal, com as medidas concentradas próximas a média (entre 9 e 11 mm).