1. Modelo Linear Simples

O modelo linear simples é utilizado para analisar a relação entre duas ou mais variáveis.

Exemplo:

Em problemas de tratamento térmico deseja-se estabelecer uma relação entre a temperatura da estufa e uma característica da qualidade (dureza) de uma peça.

---

Dureza	Temperatura
137	220
137	220
137	220
136	220
135	220
135	225
133	225
132	225
133	225
133	225
128	230
124	230
126	230
129	230
126	230
122	235
122	235
122	235
119	235
122	235

---

Faremos o upload dos dados no sistema.

Realizaremos a análise, configurando conforme a figura abaixo.

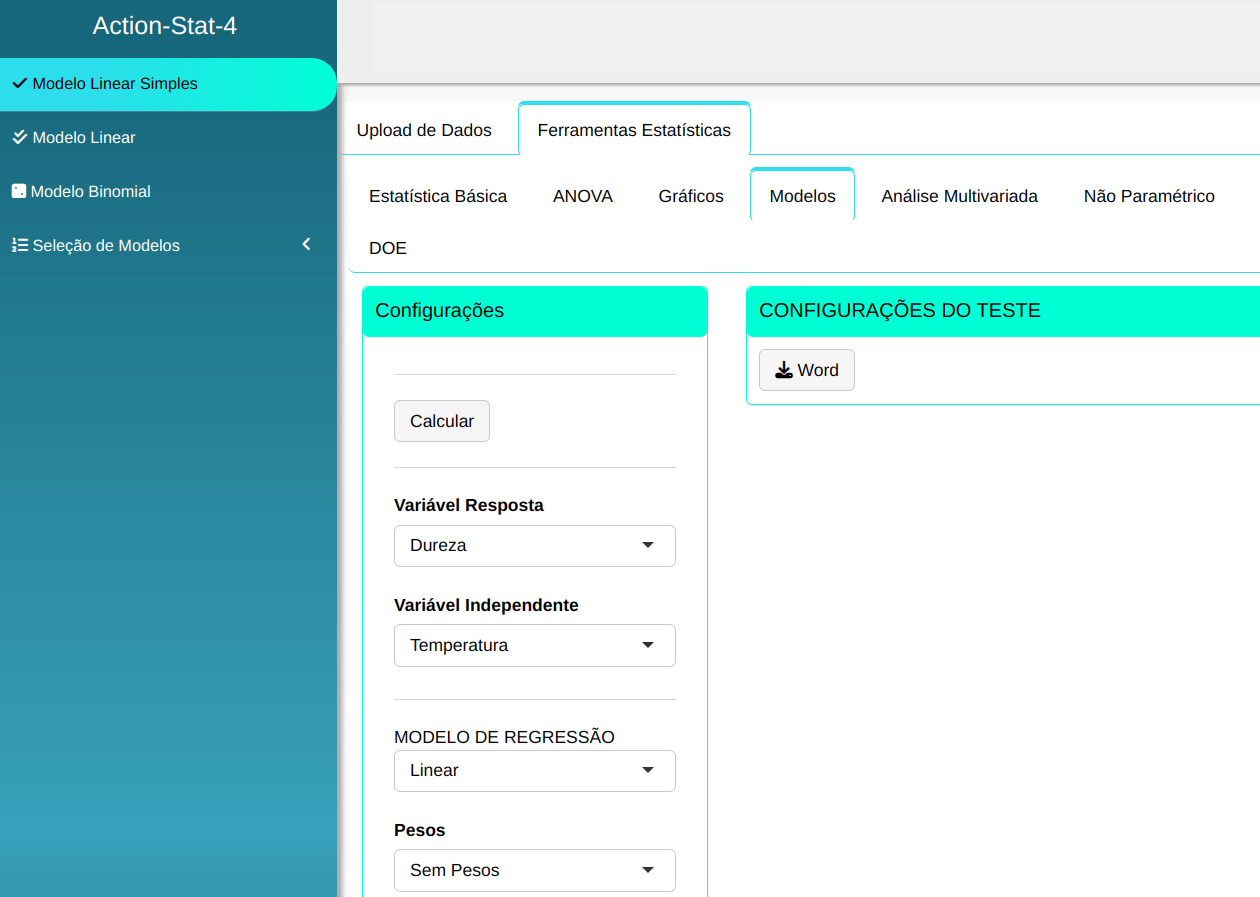
Clique em Calcular para obter os resultados. Também pode baixar os resultados no formato Word.

Os resultados são:

Tabela da ANOVA

	G.L.	Soma de Quadrados	Quadrado Médio	Estat. F	P-valor
Temperatura	1	665.64	665.640000	291.0962	0
Resíduos	18	41.16	2.286667

---

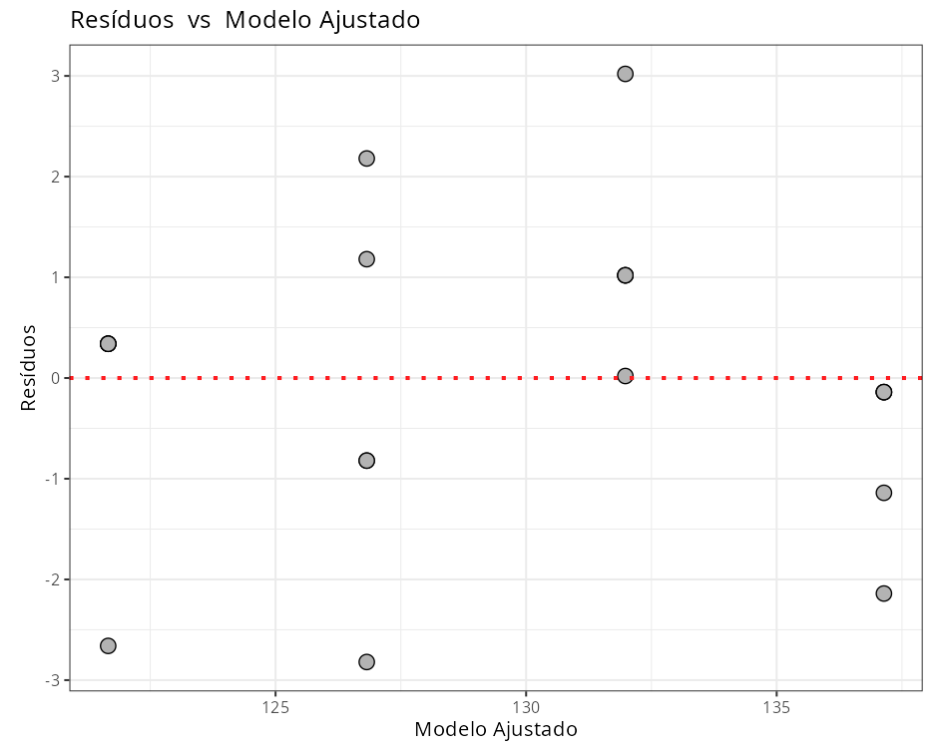
Análise Exploratória (resíduos)

Mínimo	1Q	Mediana	Média	3Q	Máximo
-2.82	-0.82	0.18	0	1.02	3.02

---

Coeficientes

	Estimativa	Desvio Padrão	Estat.t	P-valor
Intercepto	364.180	13.76492644	26.45710	0
Temperatura	-1.032	0.06048691	-17.06154	0

---

Medida Descritiva da Qualidade do Ajuste

Desvio Padrão dos Resíduos	Graus de Liberdade	$R^2$	$R^2$ Ajustado
1.512173	18	0.9417657	0.9385305

Intervalo de confiança para os parâmetros

---

	2.5 %	97.5 %
Intercepto	335.260963	393.0990373
Temperatura	-1.159078	-0.9049217

---

Intervalo de Predição

	Dureza	Temperatura	Valor Ajustado	Limite Inferior	Limite Superior	Desvio Padrão
1	137	220	137.14	135.9513	138.3287	0.5658033
2	137	220	137.14	135.9513	138.3287	0.5658033
3	137	220	137.14	135.9513	138.3287	0.5658033
4	136	220	137.14	135.9513	138.3287	0.5658033
5	135	220	137.14	135.9513	138.3287	0.5658033
6	135	225	131.98	131.2018	132.7582	0.3704052
7	133	225	131.98	131.2018	132.7582	0.3704052
8	132	225	131.98	131.2018	132.7582	0.3704052
9	133	225	131.98	131.2018	132.7582	0.3704052
10	133	225	131.98	131.2018	132.7582	0.3704052
11	128	230	126.82	126.0418	127.5982	0.3704052
12	124	230	126.82	126.0418	127.5982	0.3704052
13	126	230	126.82	126.0418	127.5982	0.3704052
14	129	230	126.82	126.0418	127.5982	0.3704052
15	126	230	126.82	126.0418	127.5982	0.3704052
16	122	235	121.66	120.4713	122.8487	0.5658033
17	122	235	121.66	120.4713	122.8487	0.5658033
18	122	235	121.66	120.4713	122.8487	0.5658033
19	119	235	121.66	120.4713	122.8487	0.5658033
20	122	235	121.66	120.4713	122.8487	0.5658033

---

Intervalo de Previsão

	Temperatura	Valor Ajustado	Limite Inferior	Limite Superior	Desvio Padrão
1	220	137.14	133.7479	140.5321	1.512173
2	220	137.14	133.7479	140.5321	1.512173
3	220	137.14	133.7479	140.5321	1.512173
4	220	137.14	133.7479	140.5321	1.512173
5	220	137.14	133.7479	140.5321	1.512173
6	225	131.98	128.7091	135.2509	1.512173
7	225	131.98	128.7091	135.2509	1.512173
8	225	131.98	128.7091	135.2509	1.512173
9	225	131.98	128.7091	135.2509	1.512173
10	225	131.98	128.7091	135.2509	1.512173
11	230	126.82	123.5491	130.0909	1.512173
12	230	126.82	123.5491	130.0909	1.512173
13	230	126.82	123.5491	130.0909	1.512173
14	230	126.82	123.5491	130.0909	1.512173
15	230	126.82	123.5491	130.0909	1.512173
16	235	121.66	118.2679	125.0521	1.512173
17	235	121.66	118.2679	125.0521	1.512173
18	235	121.66	118.2679	125.0521	1.512173
19	235	121.66	118.2679	125.0521	1.512173
20	235	121.66	118.2679	125.0521	1.512173

---

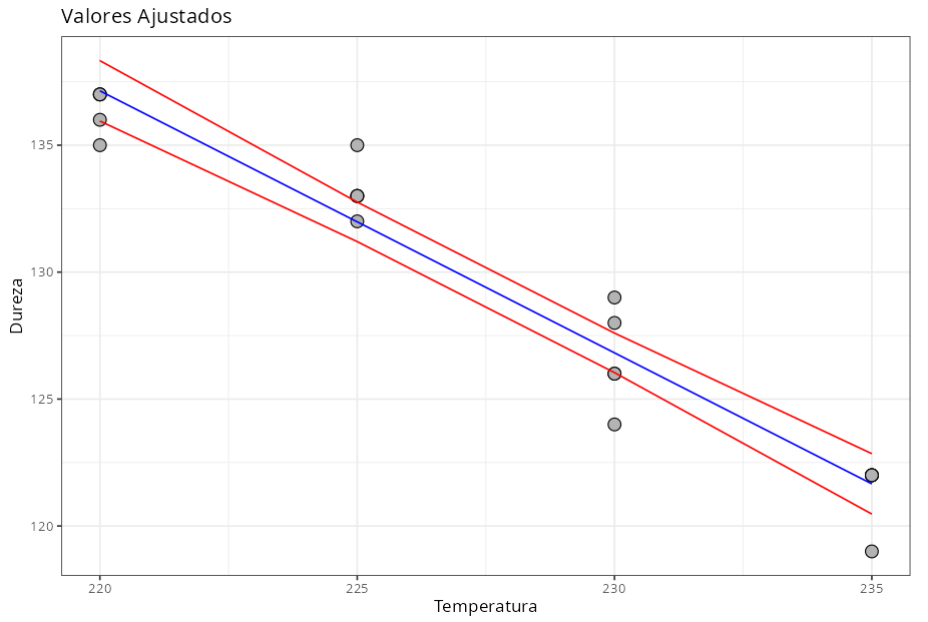
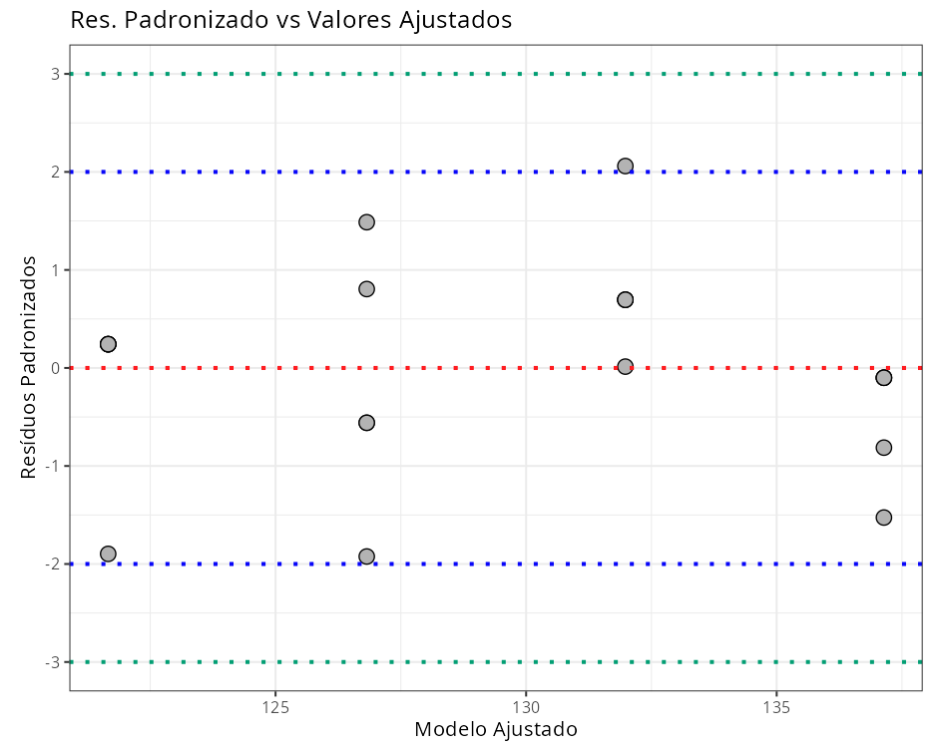
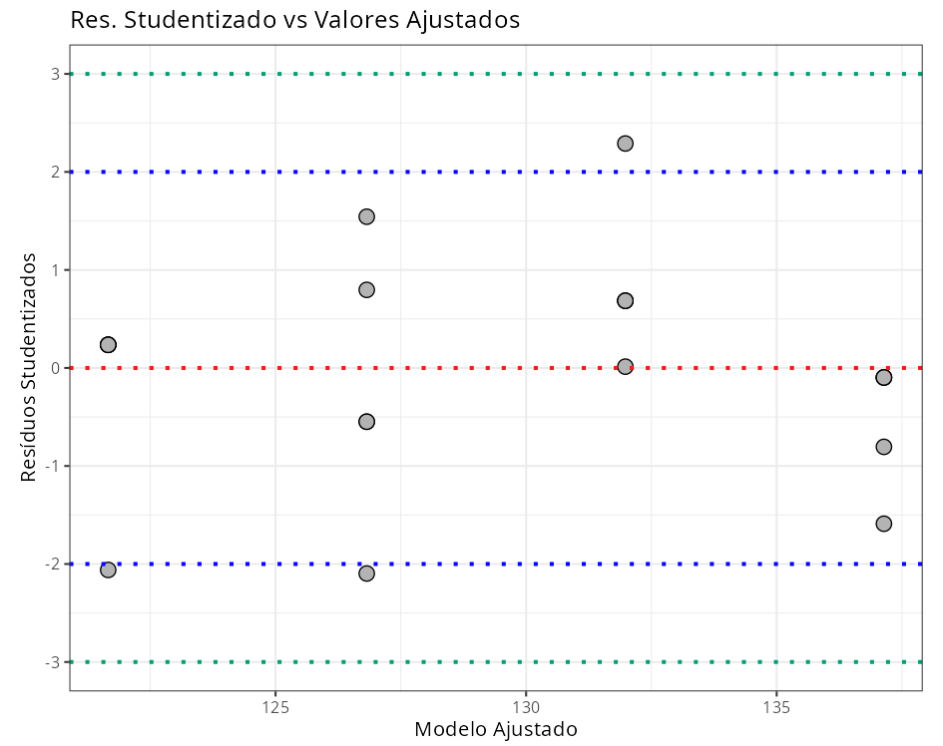
Resumo da Análise de Resíduos

N.Obs	Dureza	Temperatura	Resíduos	Resíduos Studentizados	Resíduos Padronizados	Leverage	DFFITS	DFBETA
1	137	220	-0.14	-0.09704784	-0.09983375	0.14	-0.039156210	0.031394812
2	137	220	-0.14	-0.09704784	-0.09983375	0.14	-0.039156210	0.031394812
3	137	220	-0.14	-0.09704784	-0.09983375	0.14	-0.039156210	0.031394812
4	136	220	-1.14	-0.80494250	-0.81293195	0.14	-0.324772801	0.260397546
5	135	220	-2.14	-1.58941025	-1.52603016	0.14	-0.641284585	0.514171544
6	135	225	3.02	2.28984318	2.05987841	0.06	0.578518751	-0.236179291
7	133	225	1.02	0.68539691	0.69572052	0.06	0.173162497	-0.070693294
8	132	225	0.02	0.01325730	0.01364158	0.06	0.003349398	-0.001367386
9	133	225	1.02	0.68539691	0.69572052	0.06	0.173162497	-0.070693294
10	133	225	1.02	0.68539691	0.69572052	0.06	0.173162497	-0.070693294
11	128	230	1.18	0.79664291	0.80485315	0.06	0.201268307	0.082167442
12	124	230	-2.82	-2.09718028	-1.92346262	0.06	-0.529843321	-0.216307630
13	126	230	-0.82	-0.54833211	-0.55930473	0.06	-0.138533682	-0.056556139
14	129	230	2.18	1.54290019	1.48693210	0.06	0.389806907	0.159138003
15	126	230	-0.82	-0.54833211	-0.55930473	0.06	-0.138533682	-0.056556139
16	122	235	0.34	0.23600803	0.24245339	0.14	0.095222937	0.076348201
17	122	235	0.34	0.23600803	0.24245339	0.14	0.095222937	0.076348201
18	122	235	0.34	0.23600803	0.24245339	0.14	0.095222937	0.076348201
19	119	235	-2.66	-2.06083935	-1.89684123	0.14	-0.831493637	-0.666678066
20	122	235	0.34	0.23600803	0.24245339	0.14	0.095222937	0.076348201

---

Critério

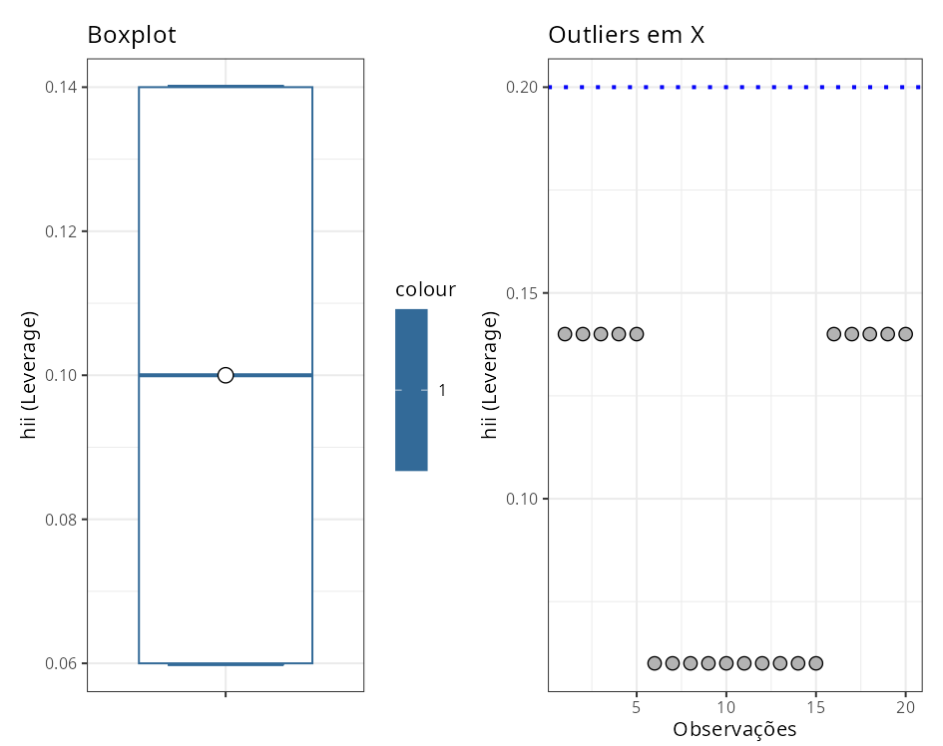
Diagnóstico	Fórmula	Valor
hii (Leverage)	(2*(p+1))/n	0.20
DFFITS	2* raíz ((p+1)/n)	0.63
DCOOK	4/n	0.20
DFBETA	2/raíz(n)	0.45
Resíduos Padronizados	(-3.3)	3.00
Resíduos Studentizados	(-3.3)	3.00

---

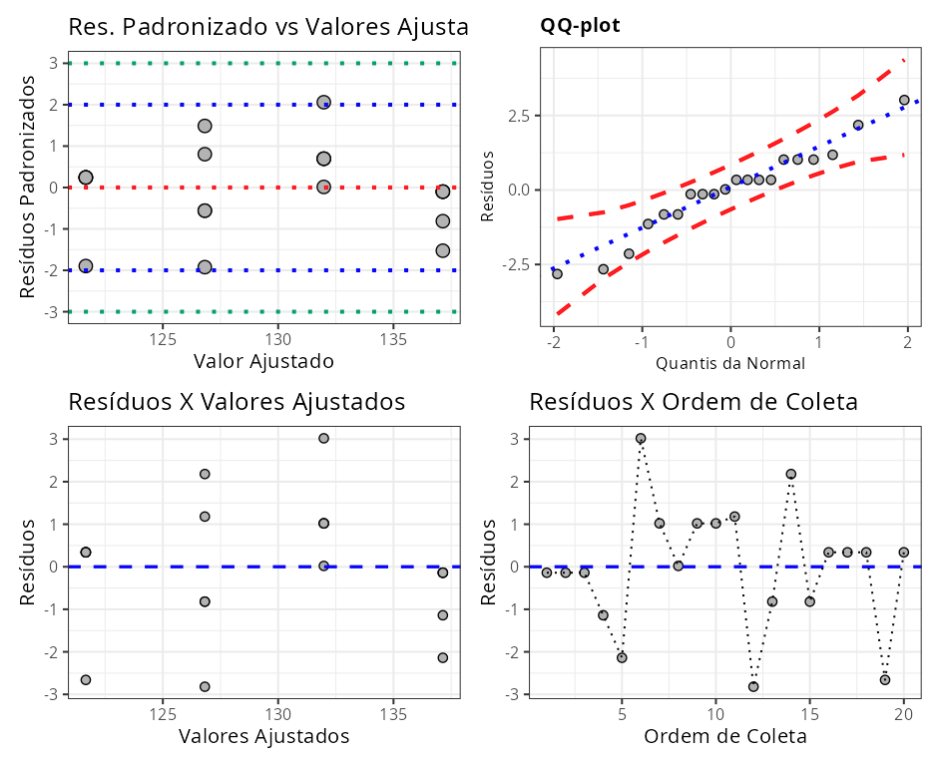
Teste de Normalidade

	Estatística	P-valor
Anderson-Darling	0.4053853	0.3202935
Shapiro-Wilk	0.9594731	0.5333777
Kolmogorov-Smirnov	0.1621102	0.1827284
Ryan-Joiner	0.9785600	0.4164000

---

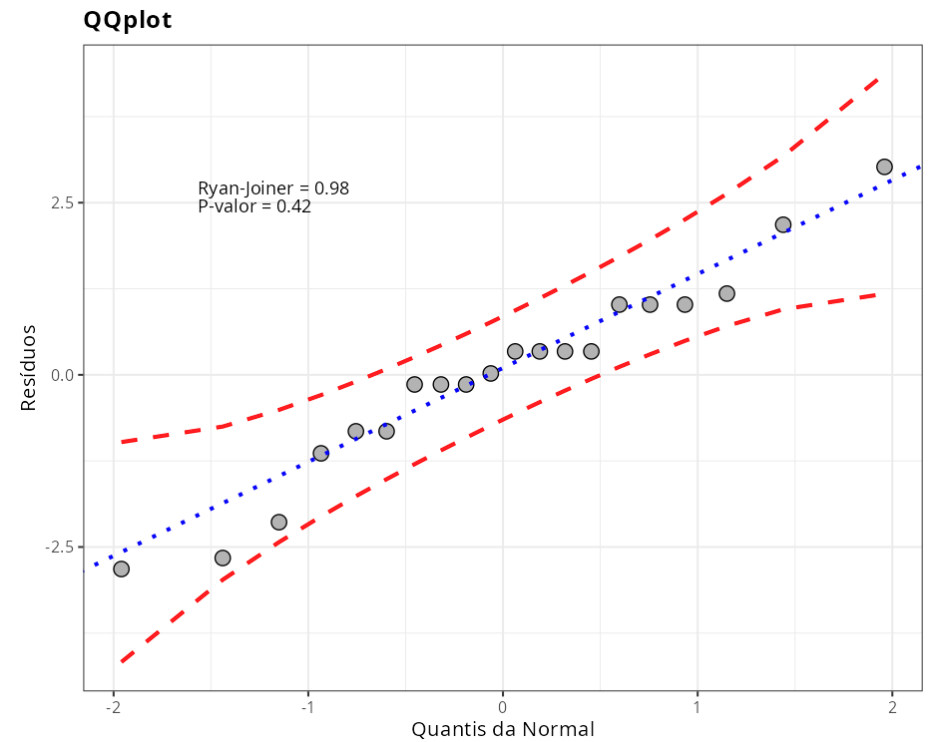
Teste de Homocedasticidade - Cochran

Estatística	Número de Réplicas	P-valor
0.5	5	0.25

---

Teste de Homocedasticidade (Brown-Forsythe)

Variável	Estatística	G.L.Num.	G.L.Den.	P-valor
Temperatura	0.6153846	3	16	0.6149536

---

Teste de Homocedasticidade - Breusch Pagan

Estatística	GL	P-valor
0.07844525	1	0.7794155

---

Teste de Homocedasticidade - Goldfeld Quandt

Variável	Estatística	GL1	GL2	P-valor
Temperatura	1.67796610169501	6	6	0.545208843765449

---

Teste de Independência - Durbin-Watson

Estatística	P-valor
2.235102	0.7686383

---

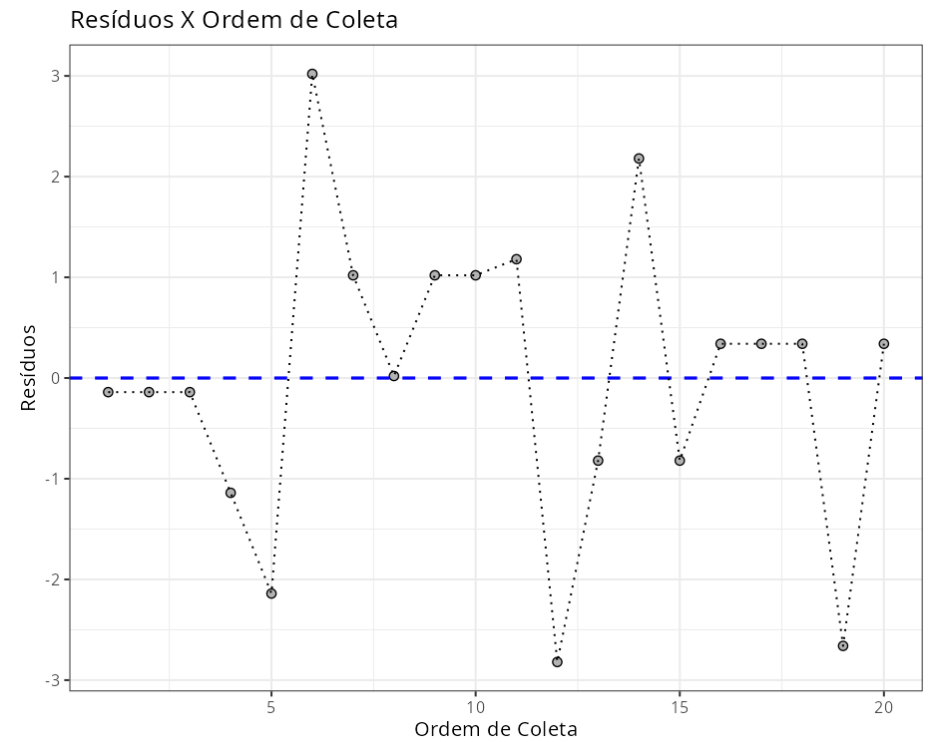
Teste de Falta de Ajuste

	GL	Soma de Quadrados	Quadrado Médio	Estat. F	P-valor
Temperatura	1	665.64	665.640000	350.336842	0
Resíduos	18	41.16	2.286667
Falta de Ajuste	2	10.76	5.38	2.831579	0.088549423924260837
Erro Puro	16	30.40	1.900000

---

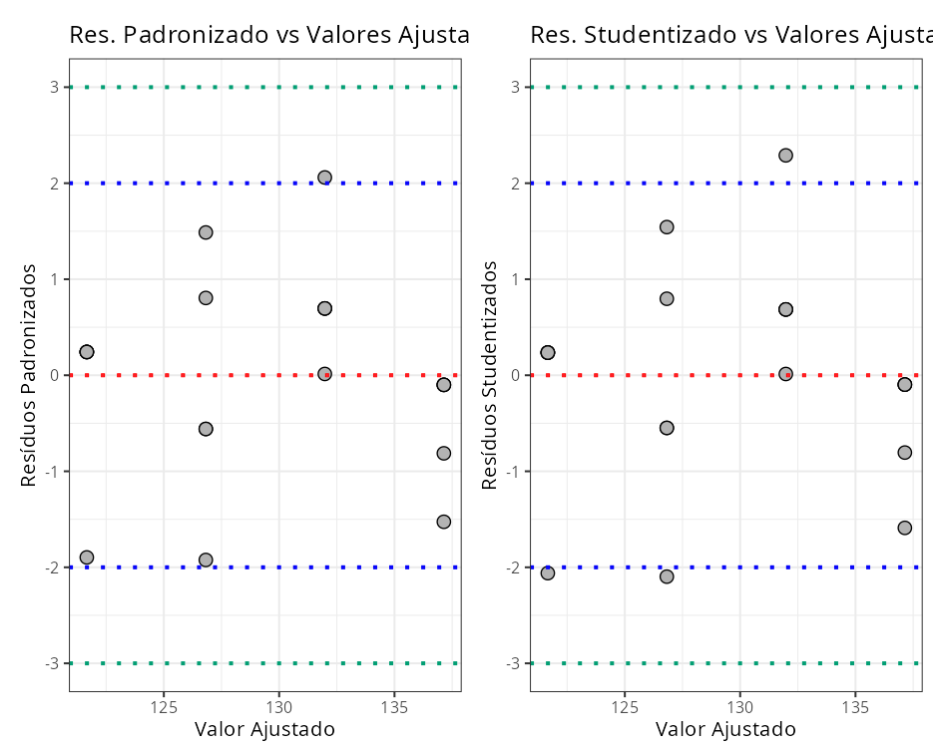
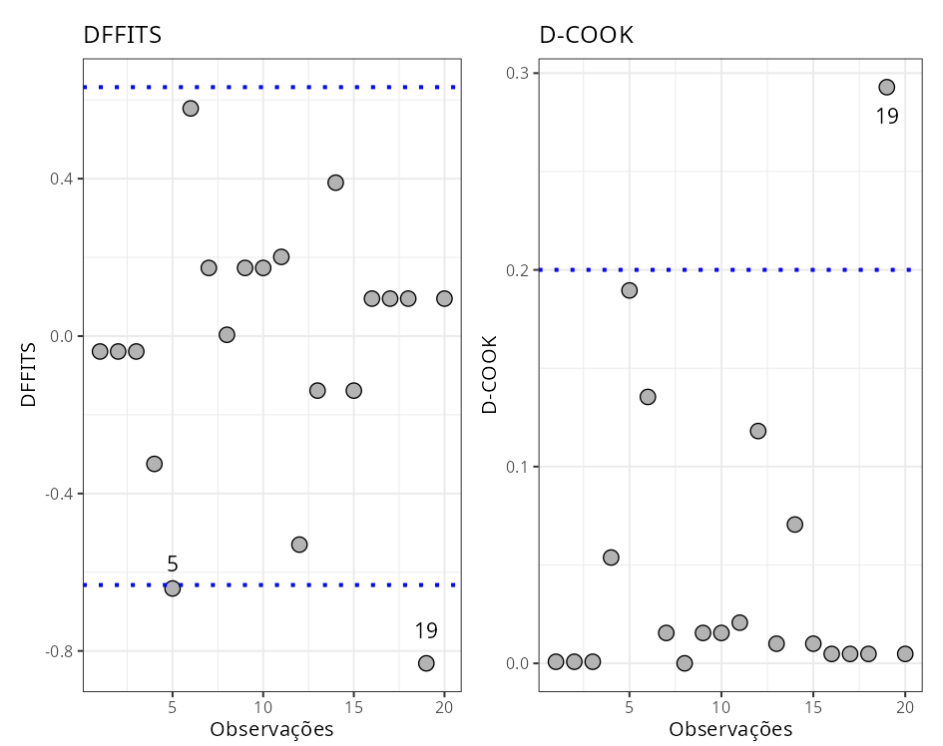
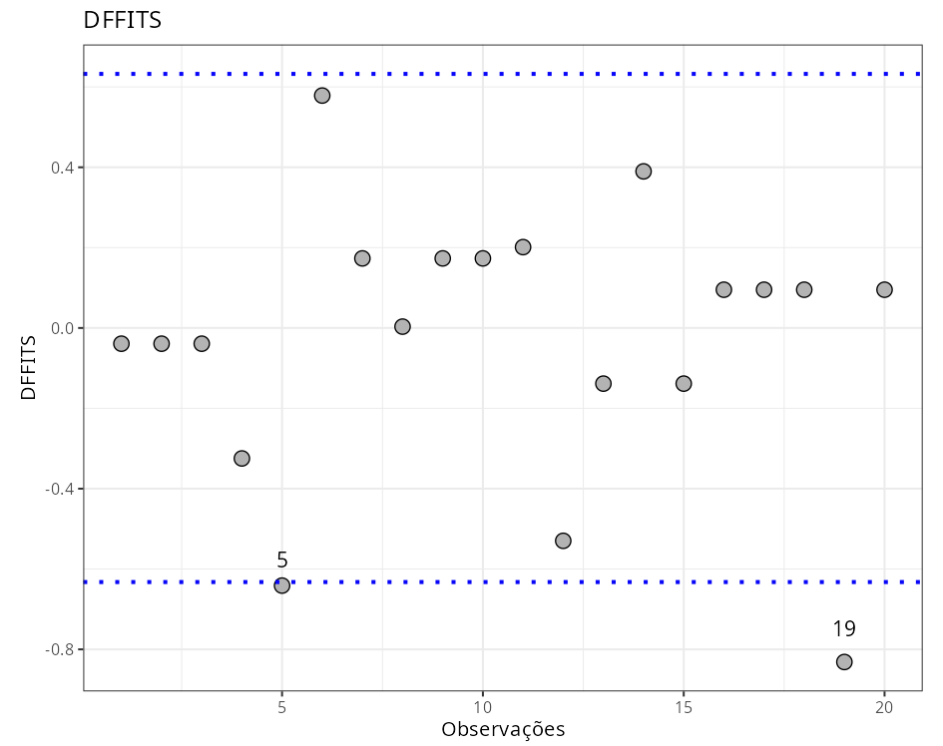
Pontos Influentes

	Observação	DFFITS	Criterio
1	5	-0.64	± 0.63
2	19	-0.83	± 0.63

---

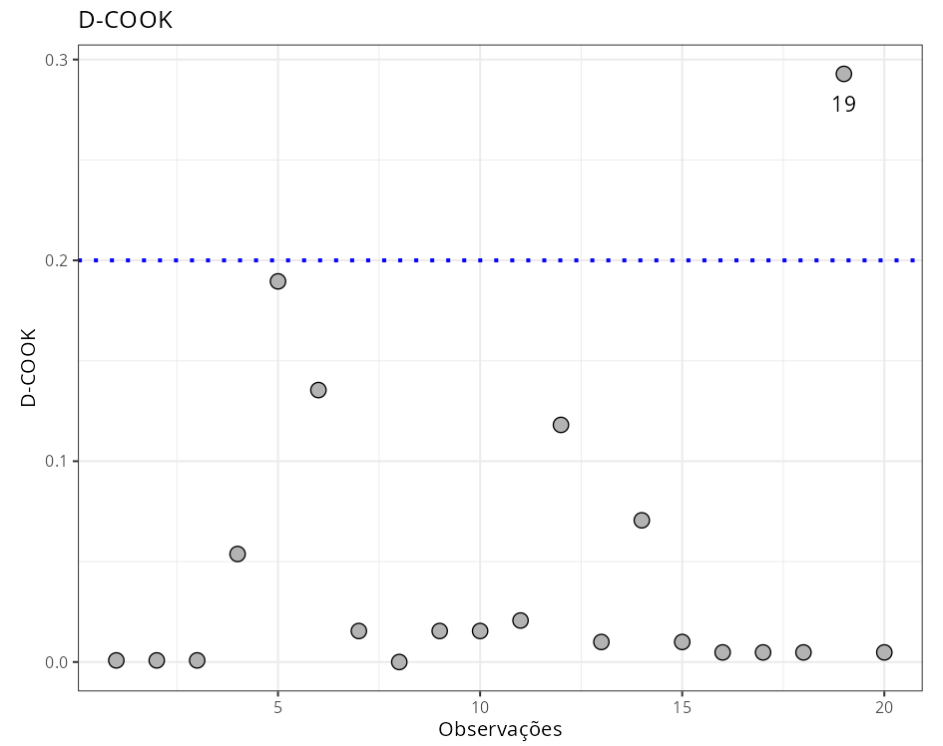
Pontos Influentes

	Observação	DCOOK	Criterio
1	19	0.2929	0.2000

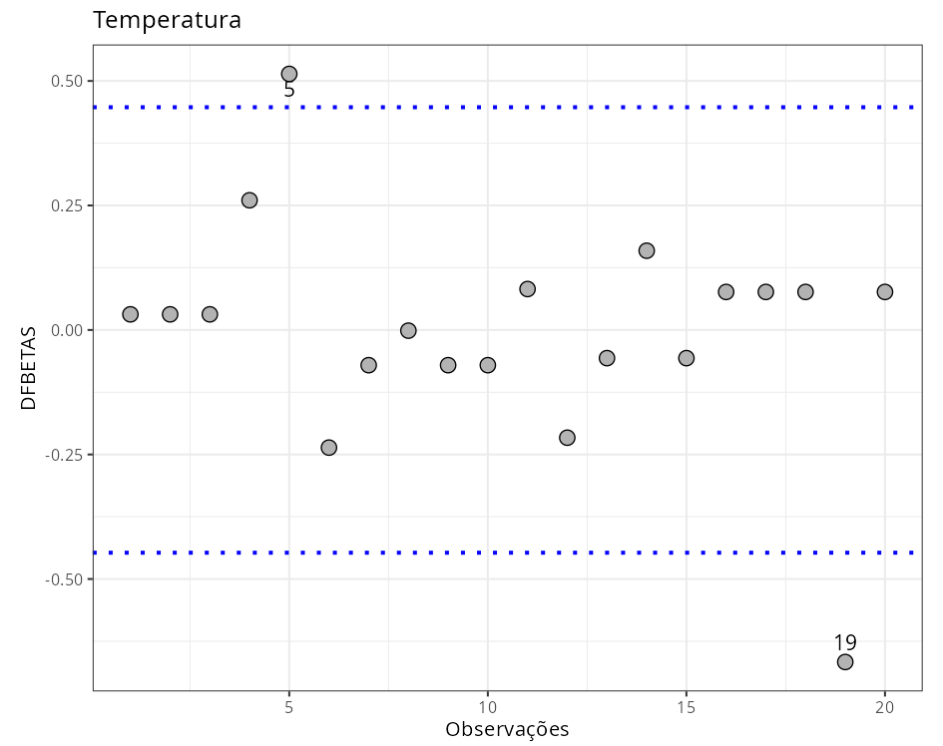
Observação	DFBETA	Critério
5	0.5141715	0.4472136
19	-0.6666781	0.4472136