2. Teste de Friedman
O Teste de Friedman é um teste não-paramétrico utilizado como uma alternativa ao teste de blocos de design aleatório na ANOVA regular. quando o pressuposto de normalidade não pode ser assegurado ou quando as variações entre os fatores são diferentes.
Exemplo:
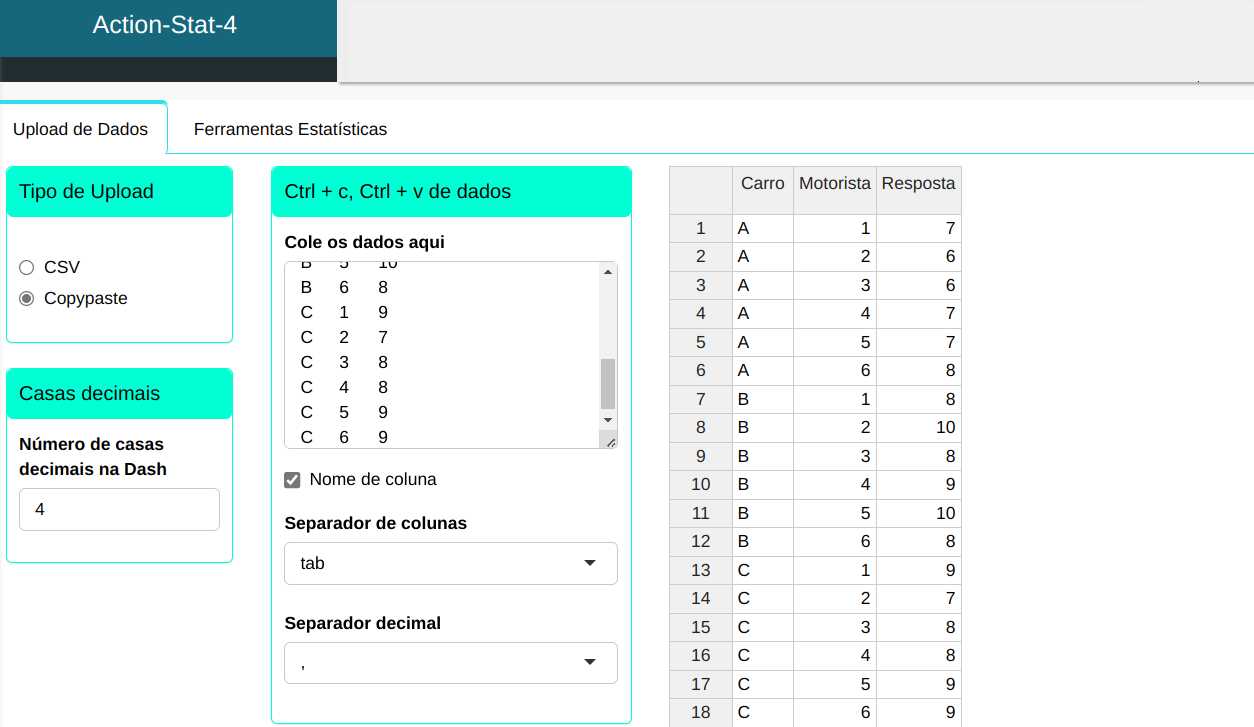
Em um estudo de avaliação de desempenho de veículos, seis motoristas analisaram três carros (A, B e C) em um experimento com design aleatório. O objetivo da pesquisa foi avaliar o desempenho dos veículos, partindo da premissa de que a marca não influencia as classificações. A tabela apresenta as notas atribuídas a cada carro por cada motorista, utilizando uma escala de 1 a 10.
| Carro | Motorista | Resposta |
|---|---|---|
| A | 1 | 7 |
| A | 2 | 6 |
| A | 3 | 6 |
| A | 4 | 7 |
| A | 5 | 7 |
| A | 6 | 8 |
| B | 1 | 8 |
| B | 2 | 10 |
| B | 3 | 8 |
| B | 4 | 9 |
| B | 5 | 10 |
| B | 6 | 8 |
| C | 1 | 9 |
| C | 2 | 7 |
| C | 3 | 8 |
| C | 4 | 8 |
| C | 5 | 9 |
| C | 6 | 9 |
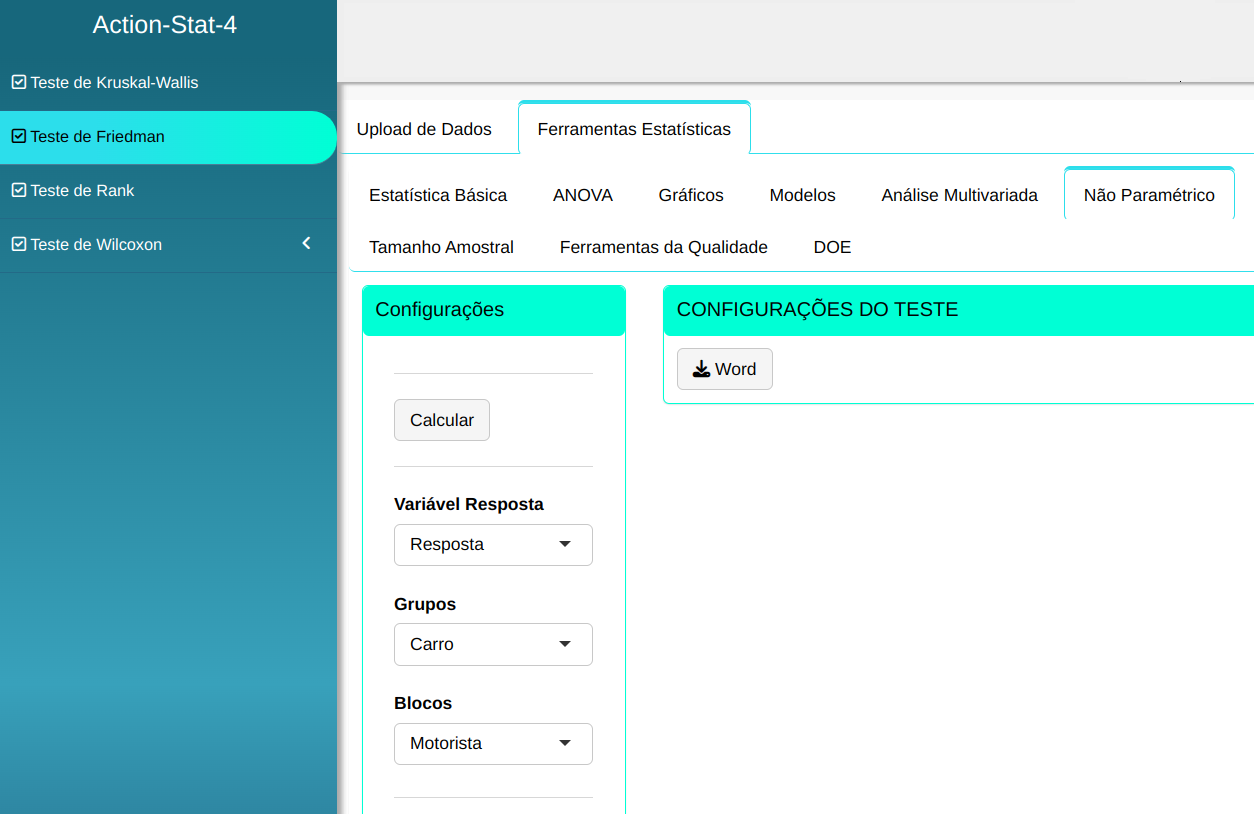
O teste de Friedman será conduzido utilizando as configurações apresentadas na figura abaixo.
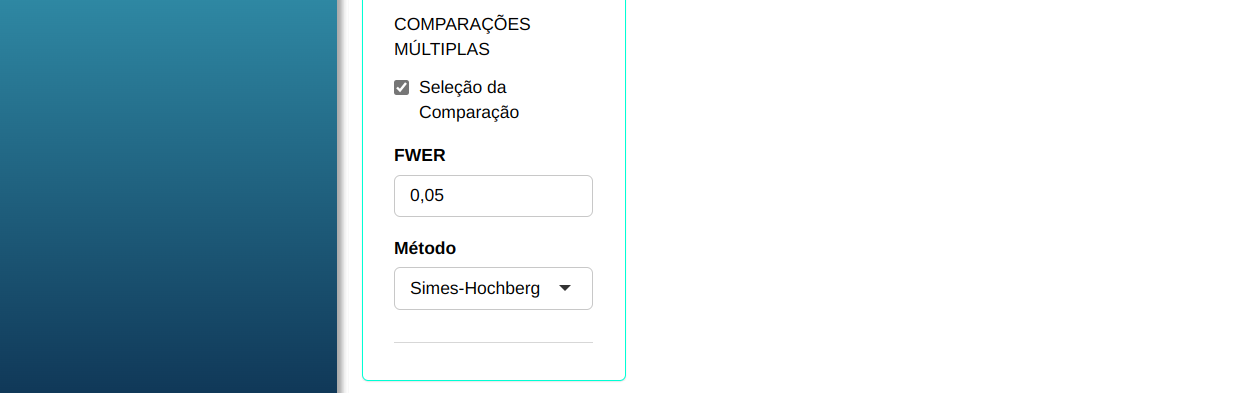
Em seguida, clique em Calcular para obter os resultados. Também pode gerar as análises e baixá-las em formato Word

Os resultados são:
Teste de Friedman
| Valor | |
|---|---|
| Friedman qui-quadrado | 8.273 |
| Graus de Liberdade | 2 |
| P-valor | 0.016 |
Tabela da Comparação Múltipla - FWER (Simes-Hochberg)
| Diferença Observada | Diferença Crítica | Estatística | P-valor | P-valor ajustado | |
|---|---|---|---|---|---|
| A - B | 8.5 | 8.293 | 2.454 | 0.014 | 0.042 |
| A - C | 8.0 | 8.293 | 2.309 | 0.021 | 0.042 |
| B - C | 0.5 | 8.293 | 0.144 | 0.885 | 0.885 |
Tabela dos Agrupamentos
| Soma (Rank) | Grupos | |
|---|---|---|
| B | 15.0 | a |
| C | 14.5 | a |
| A | 6.5 | b |
A estatística do teste é 8,273. Como o P-valor = 0,01598 < 5% então, ao nível de significância de 5% existem evidências de que os fatores não são todos iguais.
Na Tabela da Comparação Múltipla, podemos observar que existem diferenças significativas entre os fatores A e B e entre os fatores A e C.
Observando os ranks na Tabela de Agrupamento, temos que as repostas para os fatores B e C são maiores que as respostas para o fator A.