1. Teste de Kruskal-Wallis
O teste de Kruskal-Wallis é um teste de hipóteses não-paramétricos usado para comparar três ou mais populações. Ele é utilizado para testar a hipótese nula de que todas as populações têm a mesma função de distribuição contra a hipótese alternativa de que pelo menos dois deles têm diferentes funções de distribuição.
Exemplo:
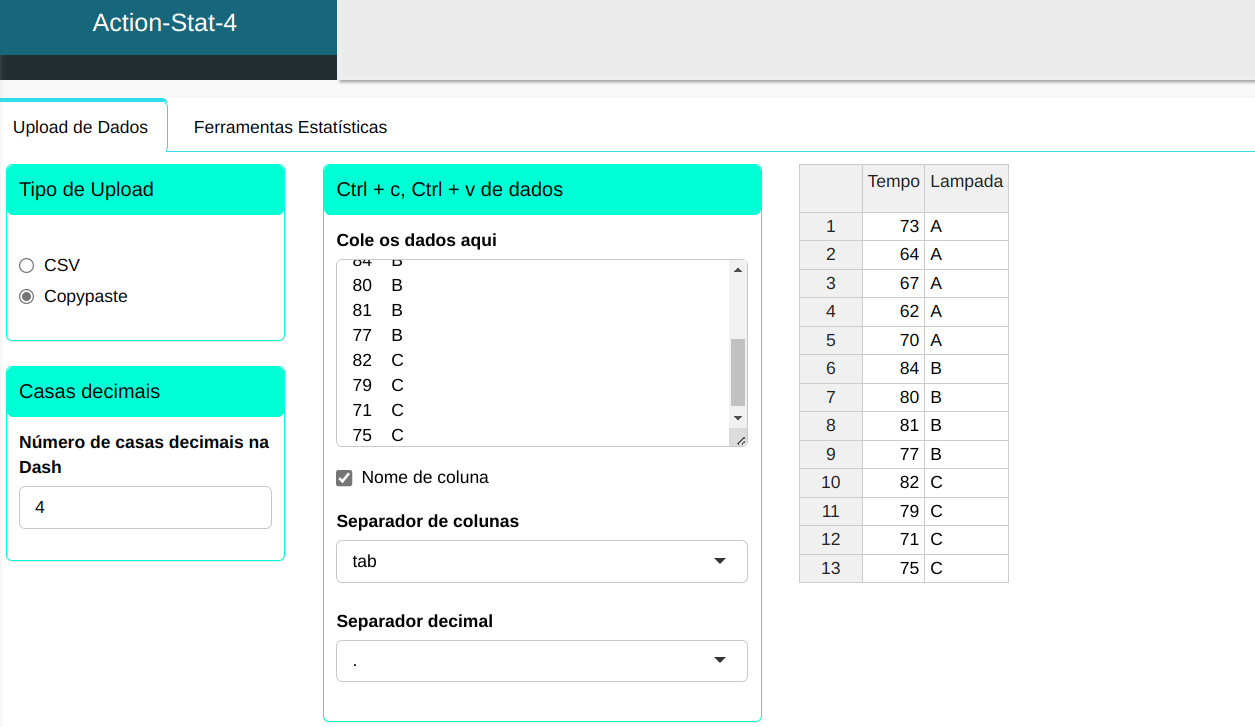
Foi selecionada uma amostra aleatória de três diferentes tipos de lâmpadas e testadas para verificar quanto tempo as lâmpadas funcionavam. faremos o upload dos resultados no sistema.
| Tempo | Lâmpada |
|---|---|
| 73 | A |
| 64 | A |
| 67 | A |
| 62 | A |
| 70 | A |
| 84 | B |
| 80 | B |
| 81 | B |
| 77 | B |
| 82 | C |
| 79 | C |
| 71 | C |
| 75 | C |
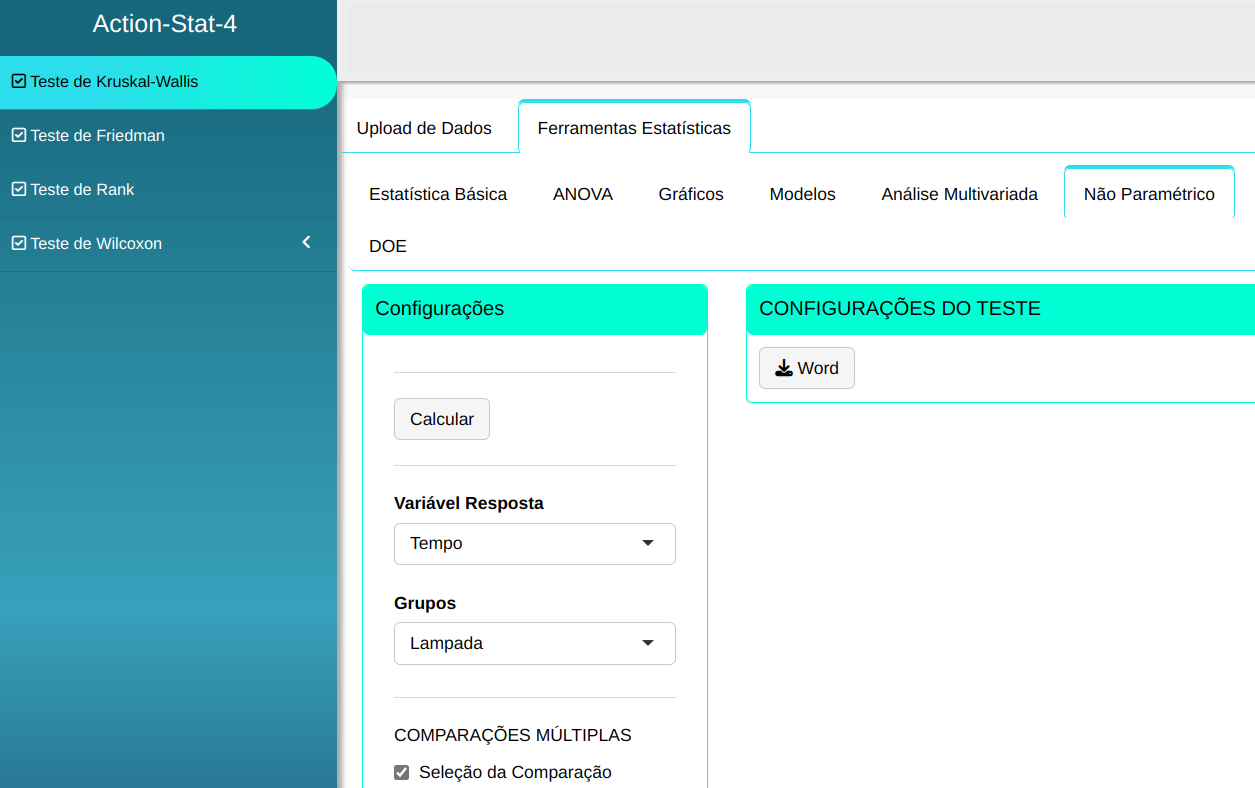
O teste o Kruskal-Wallis será conduzido utilizando as configurações apresentadas na figura abaixo.
Em seguida. clique em Calcular para obter os resultados. Também pode gerar as análises e baixá-las em formato Word.

Os resultados são:
Teste de Kruskal-Wallis
| Valor | |
|---|---|
| Kruskal-Wallis qui-quadrado | 8.403 |
| Graus de Liberdade | 2 |
| P-valor | 0.015 |
Tabela de Comparações Múltiplas - FWER (Comparação Múltipla)
| Diferença Observada | Estatística | Limite Inferior | Limite Superior | P-valor ajustado | |
|---|---|---|---|---|---|
| ''A-B'' | -7.30 | 4.659 | -10.791 | -3.809 | 0.0027 |
| ''A-C'' | -5.05 | 3.223 | -8.541 | -1.559 | 0.0183 |
| ''B-C'' | 2.25 | 1.362 | -1.430 | 5.930 | 0.203 |
Tabela dos Agrupamentos
| Médias (Rank) | Grupos | |
|---|---|---|
| B | 10.50 | a |
| C | 8.25 | a |
| A | 3.20 | b |
A estatística do teste é $\chi^2$=8,4. Como P-valor = 0,0149, rejeitamos a hipótese nula de que, em média, às três lâmpadas possuem o mesmo tempo de funcionamento. Concluímos, assim, que pelo menos uma delas possui um tempo médio de funcionamento diferente das demais.
Da tabela de Comparações Múltiplas enquanto o tempo de funcionamento das lâmpadas B e C são parecidos (P-valor do fator comparado B−C é igual a 0,20297), as lâmpadas do tipo A apresentam um tempo de funcionamento inferior aos demais tipos de lâmpadas, pois os fatores comparados A−B e A−C tem P-valores 0,0027 e 0,01825 respectivamente.