3. Teste de Rank

O Teste de Rank é o método mais popular de comparação entre curvas de sobrevivência. Esse teste é importante quando desejamos comparar um processo novo com um antigo, comparar dois produtos diferentes com relação ao tempo de vida ou ainda determinar se duas curvas de sobrevivência apresentam diferenças significativas entre si.

Exemplo 1:

Um produtor de requeijão realiza um teste de durabilidade de seu produto. O produto dele é vendido a temperatura ambiente e sem conservantes. O evento de interesse é o aparecimento de algum fungo no produto. Os dados são apresentados abaixo, sendo o tempo medido em horas. O símbolo + indica censura.

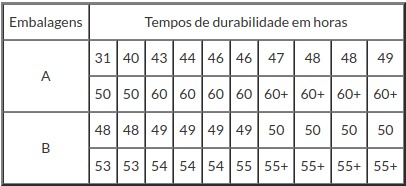
Existe diferença entre às duas embalagens com relação à durabilidade do produto? Vamos comparar os tempos de durabilidade usando o Teste de Rank.

Primeiramente vamos organizar os dados numa nova tabela, em que substituímos o símbolo + pelo indicador 0 (censura) e para os demais valores colocamos o indicador 1 (falha).

Tempos	Censura	Grupo
31	1	A
40	1	A
43	1	A
44	1	A
46	1	A
46	1	A
47	1	A
48	1	A
48	1	A
49	1	A
50	1	A
50	1	A
60	1	A
60	1	A
60	1	A
60	1	A
60	0	A
60	0	A
60	0	A
60	0	A
48	1	B
48	1	B
49	1	B
49	1	B
49	1	B
49	1	B
50	1	B
50	1	B
50	1	B
50	1	B
53	1	B
53	1	B
54	1	B
54	1	B
54	1	B
55	1	B
55	0	B
55	0	B
55	0	B
55	0	B

---

Faremos o upload dos dados no sistema.

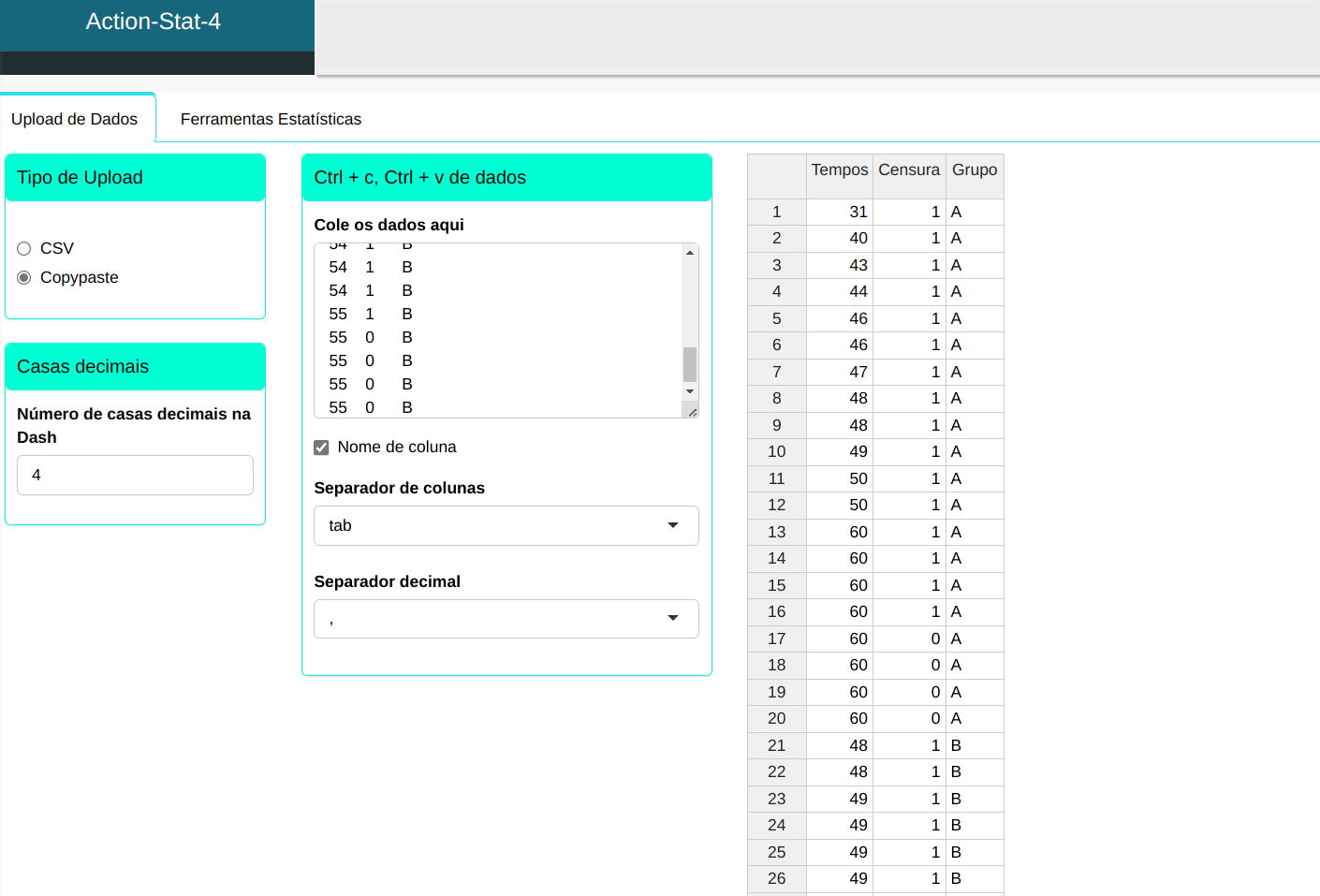
O teste de Rank será conduzido utilizando as configurações apresentadas na figura abaixo.

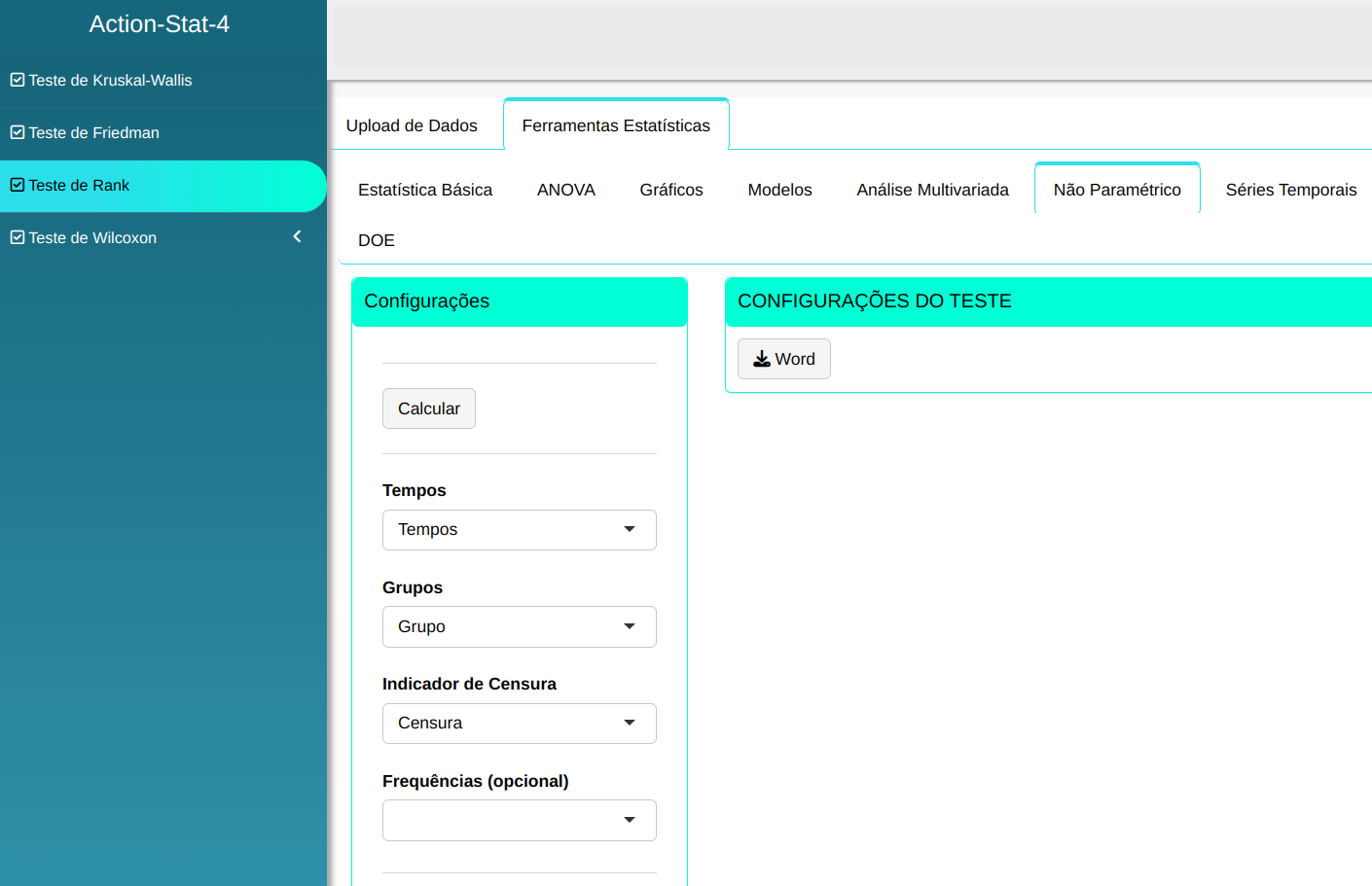
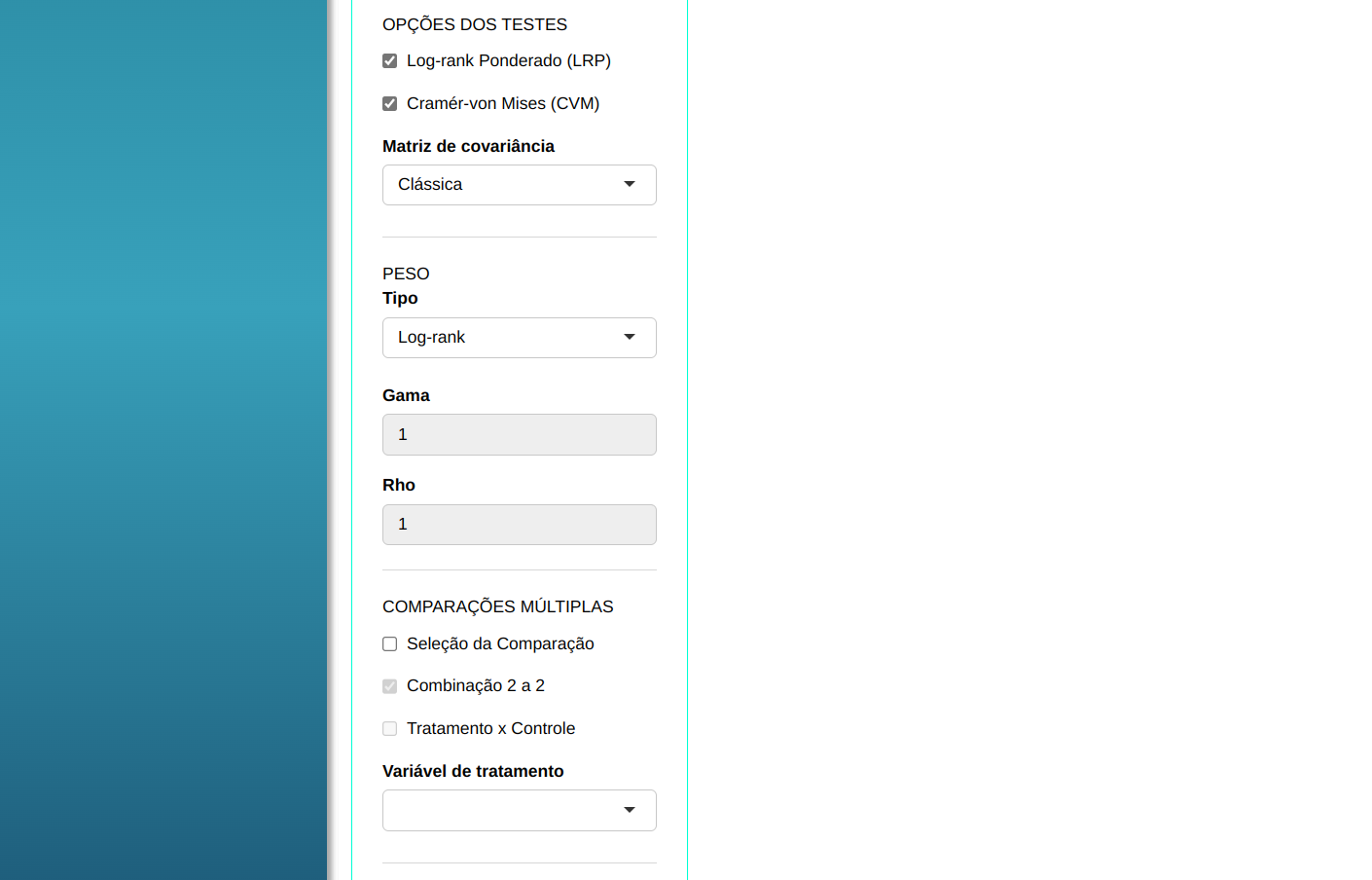
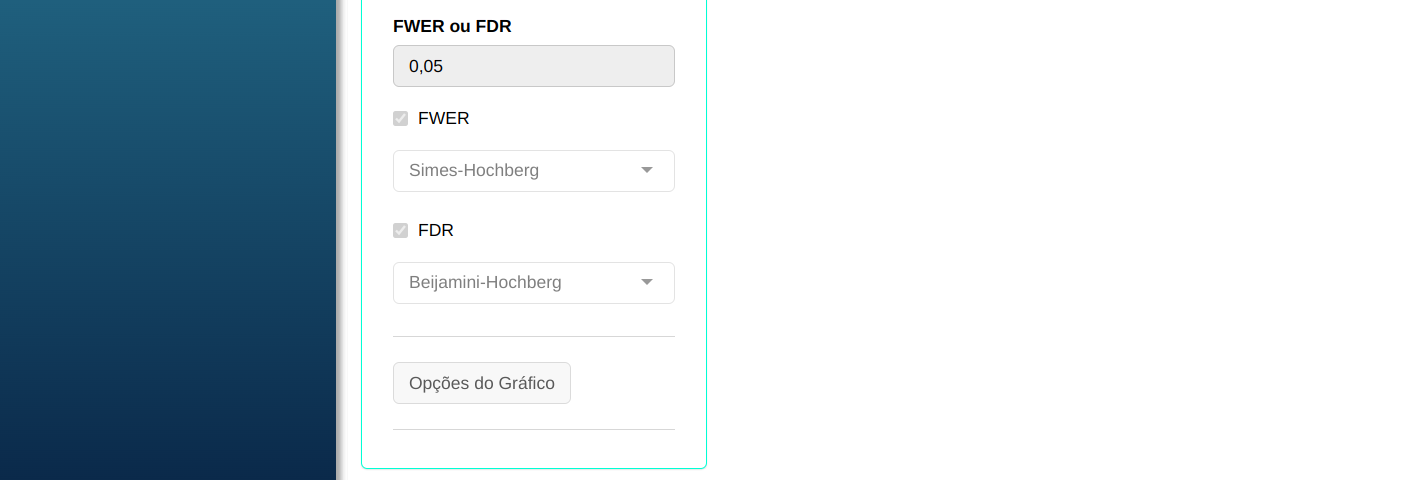
Clicando em calcular obteremos os resultados e também pode baixar os resultados em um arquivo do Word.

Os resultados são:

Comparação dos grupos

	Peso	Estatística	P-valor
Cramér-von Mises (CVM) 1	LogRank	47.473	0.110
Log-rank Ponderado (LRP) 1	LogRank	0.006	0.936

---

Resumo da comparação dos grupos

Grupos	Tempo	Número de eventos	Quantidade em risco	Desvio Padrão	Função Sobrevivência	Limite inferior	Limite superior	Função de Intensidade	Limite inferior.1	Limite superior.1
A	31.0000	1.0000	20.0000	0.0487	0.9500	0.8540	1.0000	0.0500	0.0452	0.0548
A	40.0000	1.0000	19.0000	0.0671	0.9000	0.7690	1.0000	0.1000	0.0869	0.1131
A	43.0000	1.0000	18.0000	0.0798	0.8500	0.6940	1.0000	0.1500	0.1265	0.1735
A	44.0000	1.0000	17.0000	0.0894	0.8000	0.6250	0.9750	0.2000	0.1649	0.2351
A	46.0000	2.0000	16.0000	0.1020	0.7000	0.4990	0.9010	0.3000	0.2397	0.3603
A	47.0000	1.0000	14.0000	0.1070	0.6500	0.4410	0.8590	0.3500	0.2768	0.4232
A	48.0000	2.0000	13.0000	0.1110	0.5500	0.3320	0.7680	0.4500	0.3519	0.5481
A	49.0000	1.0000	11.0000	0.1120	0.5000	0.2810	0.7190	0.5000	0.3904	0.6096
A	50.0000	2.0000	10.0000	0.1100	0.4000	0.1850	0.6150	0.6000	0.4712	0.7288
A	60.0000	4.0000	8.0000	0.0894	0.2000	0.0247	0.3750	0.8000	0.6598	0.9402
B	48.0000	2.0000	20.0000	0.0671	0.9000	0.7690	1.0000	0.1000	0.0869	0.1131
B	49.0000	4.0000	18.0000	0.1020	0.7000	0.4990	0.9010	0.3000	0.2397	0.3603
B	50.0000	4.0000	14.0000	0.1120	0.5000	0.2810	0.7190	0.5000	0.3904	0.6096
B	53.0000	2.0000	10.0000	0.1100	0.4000	0.1850	0.6150	0.6000	0.4712	0.7288
B	54.0000	3.0000	8.0000	0.0968	0.2500	0.0602	0.4400	0.7500	0.6077	0.8923
B	55.0000	1.0000	5.0000	0.0894	0.2000	0.0247	0.3750	0.8000	0.6598	0.9402

---

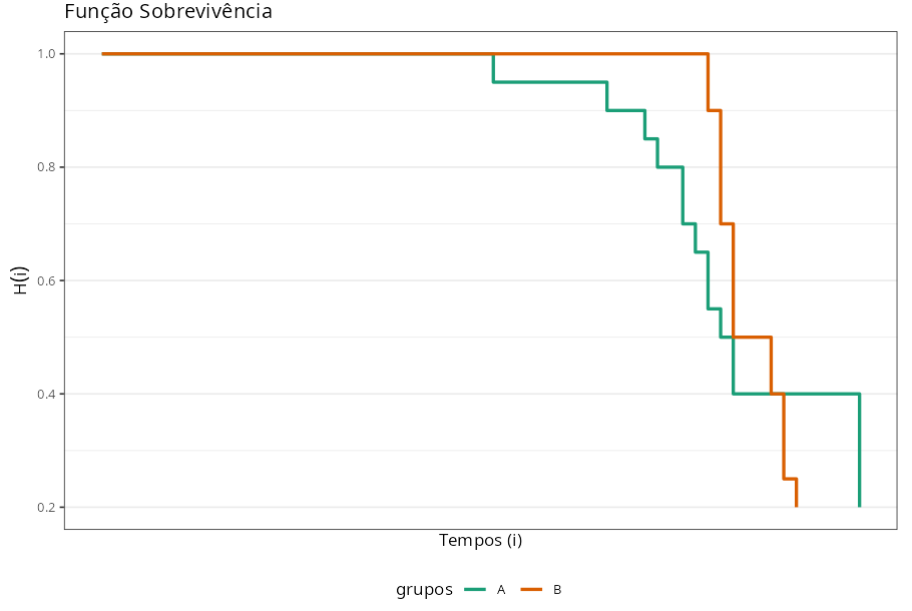
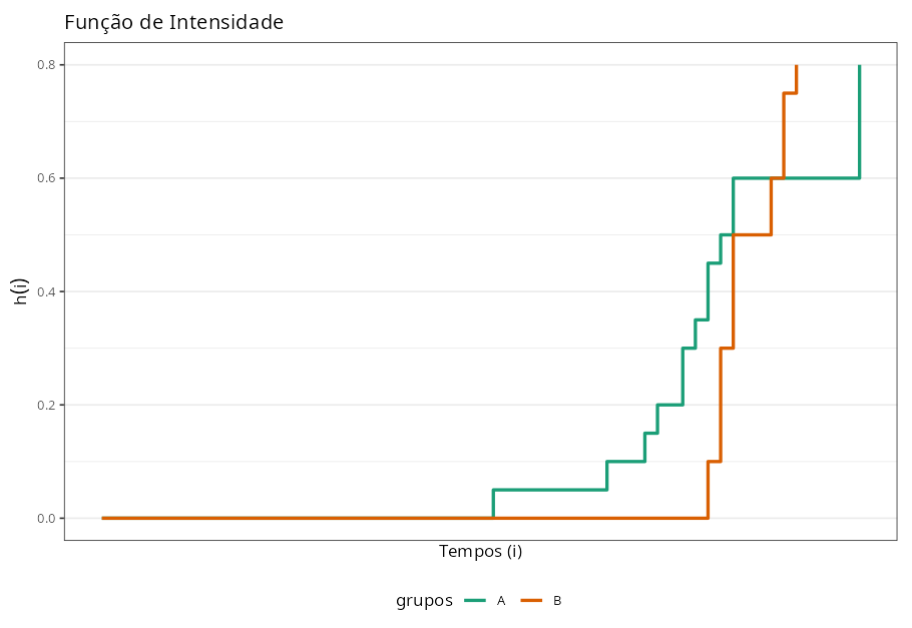
Sabendo que o Teste de Rank é utilizado para testar a hipótese nula de que não há diferença entre os grupos (A e B) concluímos que, de acordo com o p-valor de 0,9362, não devemos rejeitar a hipótese nula. Assim, dizemos que não há diferença significativa entre às duas embalagens com relação á durabilidade do produto.

Exemplo 2:

Um produtor de requeijão realiza um teste de durabilidade de seu produto. O produto dele é vendido a temperatura ambiente e sem conservantes. O evento de interesse é o aparecimento de algum fungo no produto. Os dados são apresentados abaixo, sendo o tempo medido em horas. O símbolo + indica censura.

Existe diferença entre às duas embalagens com relação à durabilidade do produto? Vamos comparar os tempos de durabilidade usando o Teste de Rank.

Para trabalhar com dados resumidos devemos montar a seguinte tabela:

Tempos	Censura	Grupo	Frequência
31	1	A	1
40	1	A	1
43	1	A	1
44	1	A	1
46	1	A	2
47	1	A	1
48	1	A	2
48	1	B	2
49	1	A	1
49	1	B	4
50	1	A	2
50	1	B	4
53	1	B	2
54	1	B	3
55	1	B	1
55	0	B	4
60	1	A	4
60	0	A	4

---

Faremos o upload da tabela no sistema.

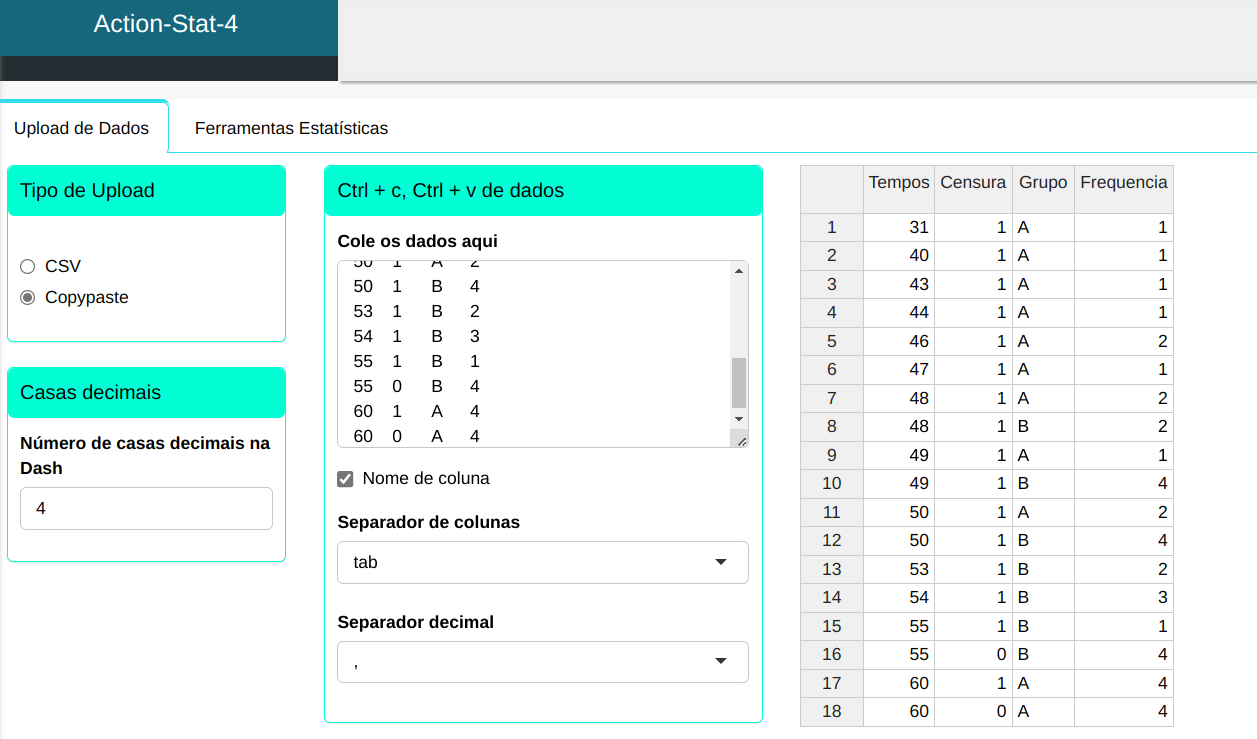
O teste de Rank será conduzido utilizando as configurações apresentadas na figura abaixo.

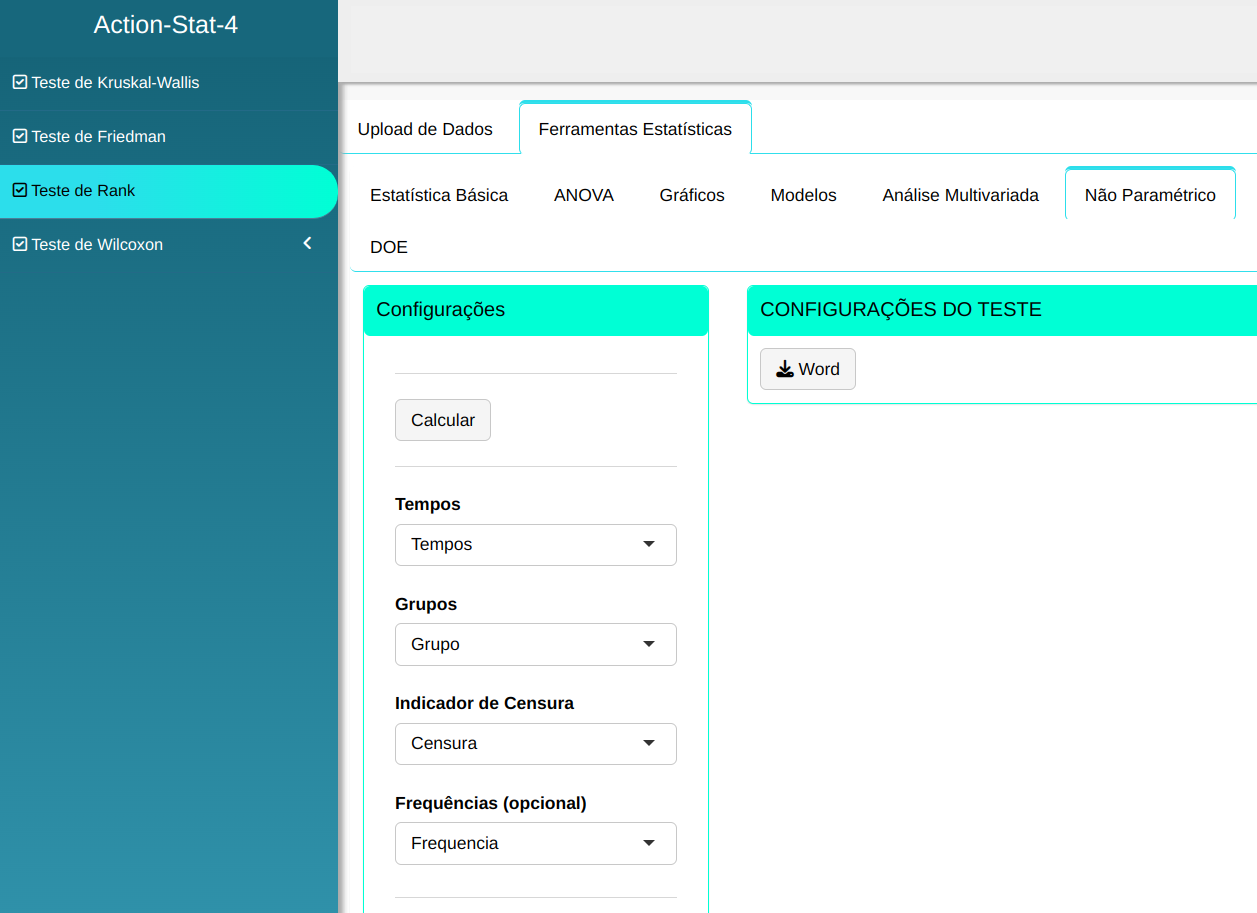
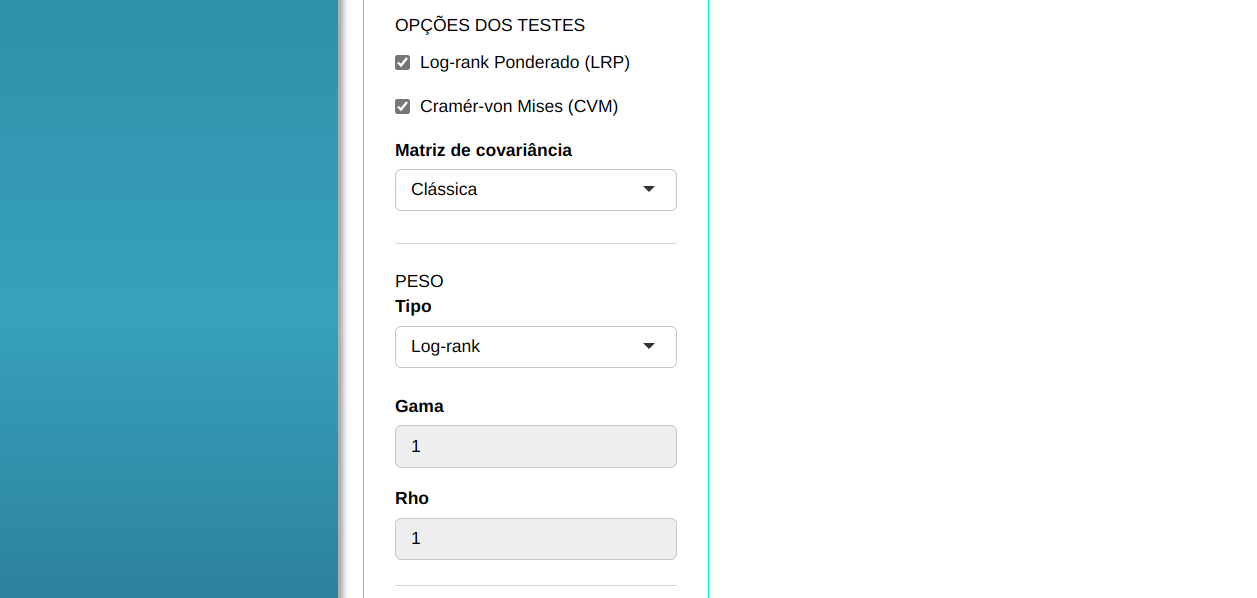
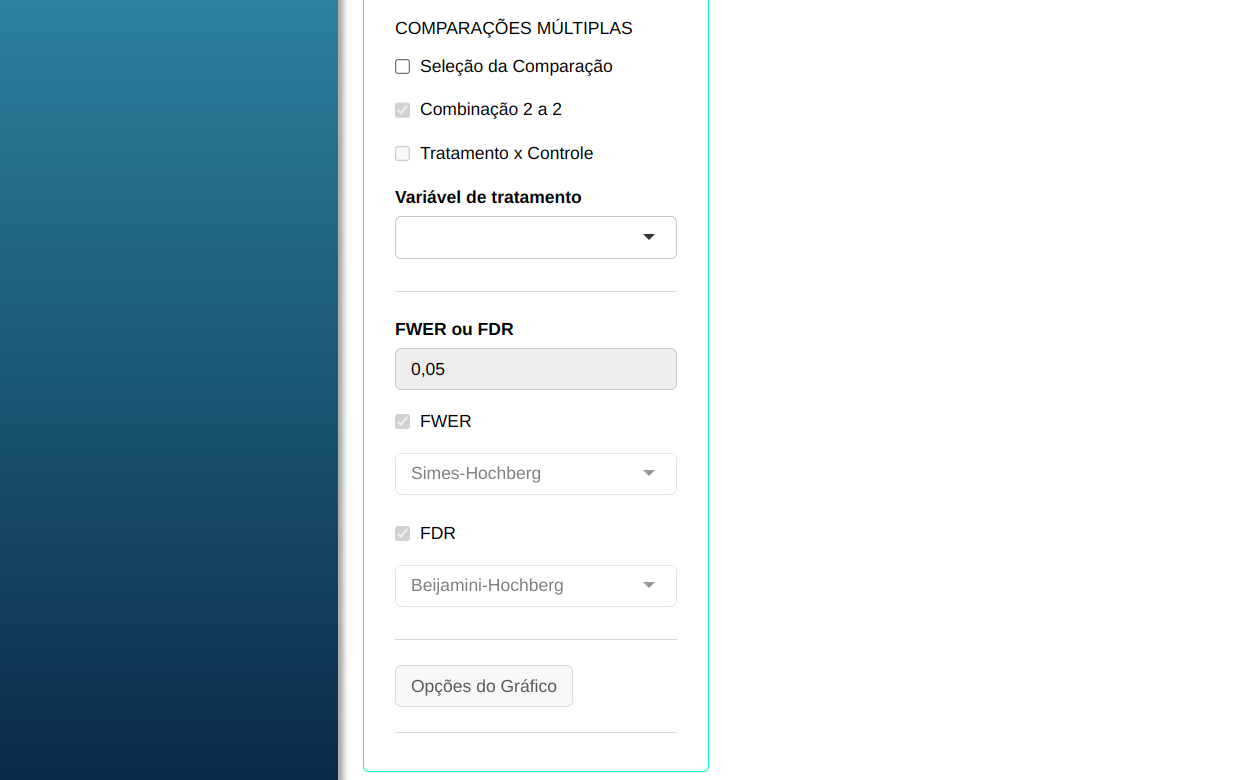
Clicando em calcular obteremos os resultados e também pode baixar os resultados em um arquivo do Word.

Os resultados são:

Comparação dos grupos

	Peso	Estatística	P-valor
Cramér-von Mises (CVM) 1	LogRank	47.473	0.110
Log-rank Ponderado (LRP) 1	LogRank	0.006	0.936

---

Resumo da comparação dos grupos

Grupos	Tempo	Número de eventos	Quantidade em risco	Desvio Padrão	Função Sobrevivência	Limite inferior	Limite superior	Função de Intensidade	Limite inferior 1	Limite superior 1
A	31	1	20	0.049	0.95	0.854	1	0.05	0.045	0.055
A	40	1	19	0.067	0.9	0.769	1	0.1	0.087	0.113
A	43	1	18	0.08	0.85	0.694	1	0.15	0.127	0.173
A	44	1	17	0.089	0.8	0.625	0.975	0.2	0.165	0.235
A	46	2	16	0.102	0.7	0.499	0.901	0.3	0.24	0.36
A	47	1	14	0.107	0.65	0.441	0.859	0.35	0.277	0.423
A	48	2	13	0.111	0.55	0.332	0.768	0.45	0.352	0.548
A	49	1	11	0.112	0.5	0.281	0.719	0.5	0.39	0.61
A	50	2	10	0.11	0.4	0.185	0.615	0.6	0.471	0.729
A	60	4	8	0.089	0.2	0.025	0.375	0.8	0.66	0.94
B	48	2	20	0.067	0.9	0.769	1	0.1	0.087	0.113
B	49	4	18	0.102	0.7	0.499	0.901	0.3	0.24	0.36
B	50	4	14	0.112	0.5	0.281	0.719	0.5	0.39	0.61
B	53	2	10	0.11	0.4	0.185	0.615	0.6	0.471	0.729
B	54	3	8	0.097	0.25	0.06	0.44	0.75	0.608	0.892
B	55	1	5	0.089	0.2	0.025	0.375	0.8	0.66	0.94

---

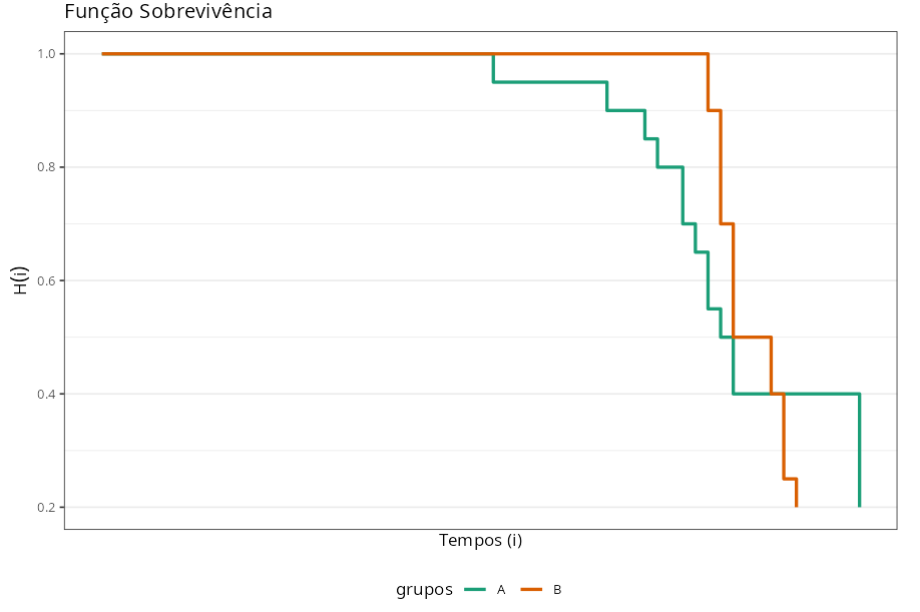
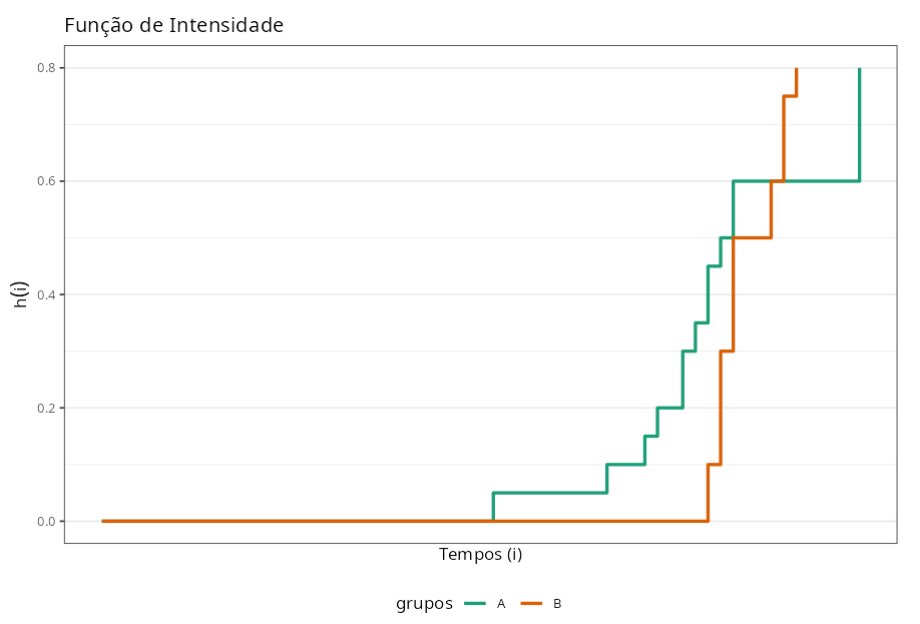
Sabendo que o teste de Rank é utilizado para testar a hipótese nula de que não há diferença entre os grupos (A e B) concluímos que de acordo com o p-valor de 0,5399. não devemos rejeitar a hipótese nula. Assim, dizemos que não há diferença significativa entre as duas embalagens com relação a durabilidade do produto.