4. Teste de Wilcoxon
Através do teste de Wilcoxon, testamos as pseudo mediana, para amostra única. amostras independentes e pareado.
Exemplo 1:
Supondo que os números da amostra são distribuídos simetricamente em torno da mediana, usaremos o teste de Wilcoxon para testar a hipótese $H_0$: $\theta_0$ = 220 de que a mediana é igual a 220, ao nível de significância de 5%.
| Dados |
|---|
| 126 |
| 142 |
| 156 |
| 228 |
| 245 |
| 246 |
| 370 |
| 419 |
| 433 |
| 454 |
| 478 |
| 503 |
O teste de Wilcoxon será conduzido utilizando as configurações apresentadas na figura abaixo.
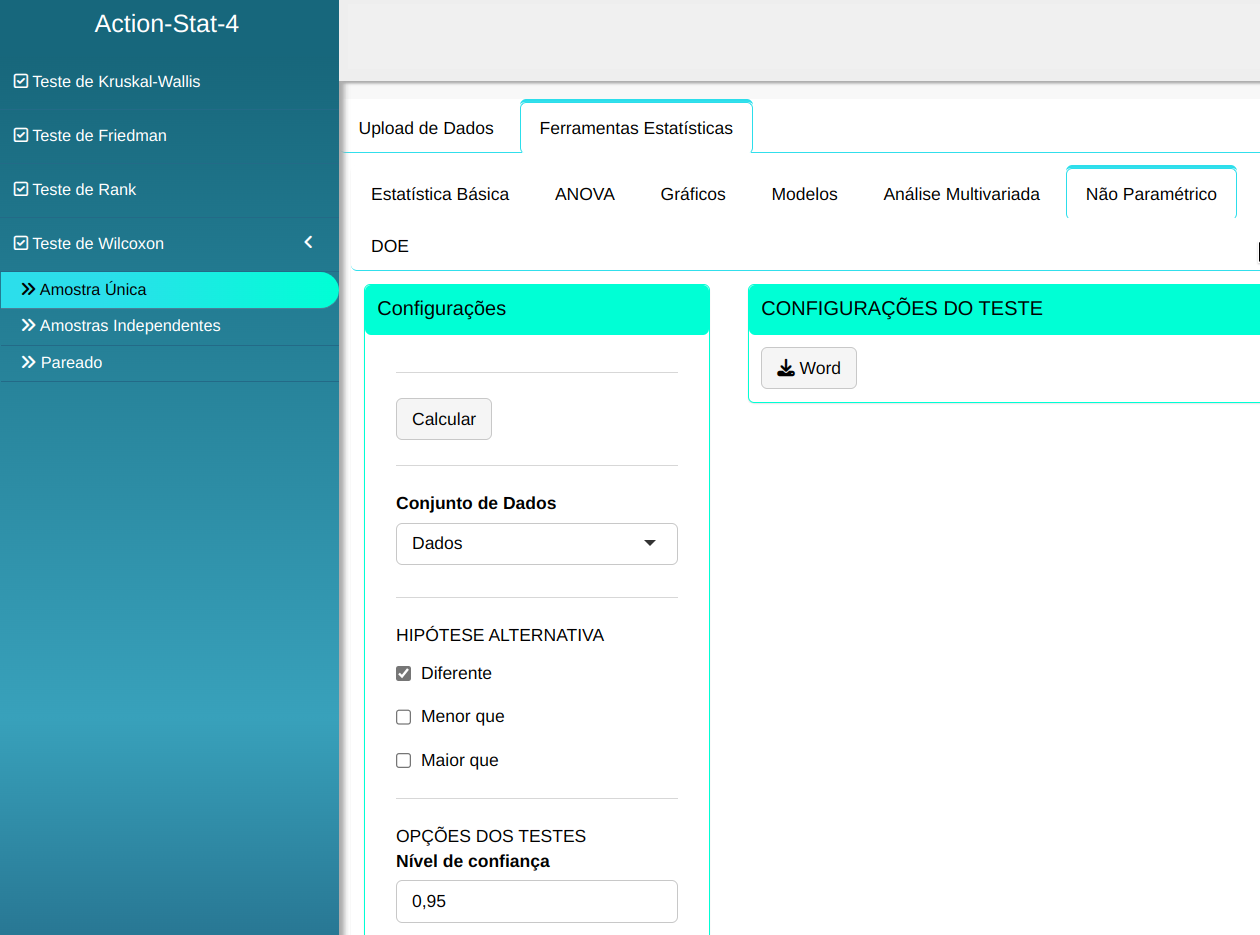
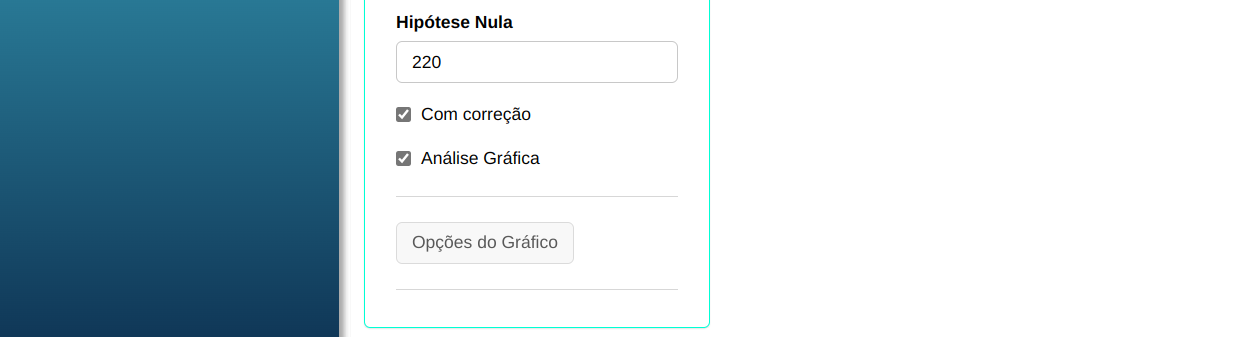
Clicando em Calcular obtemos os resultados e também é possível gerar a análise e baixar em formato Word.

Os resultados são:
Tabela da Estatística do Teste (Wilcoxon)
| Valores | |
|---|---|
| Estatística | 63 |
| P-valor | 0.064 |
| Hipótese Nula | 220 |
| Limite Inferior | 200.5 |
| (Pseudo) Mediana | 315.75 |
| Limite Superior | 433 |
| Nível de Confiança | 0.95 |
Gráfico do teste de Wilcoxon - Amostra Única
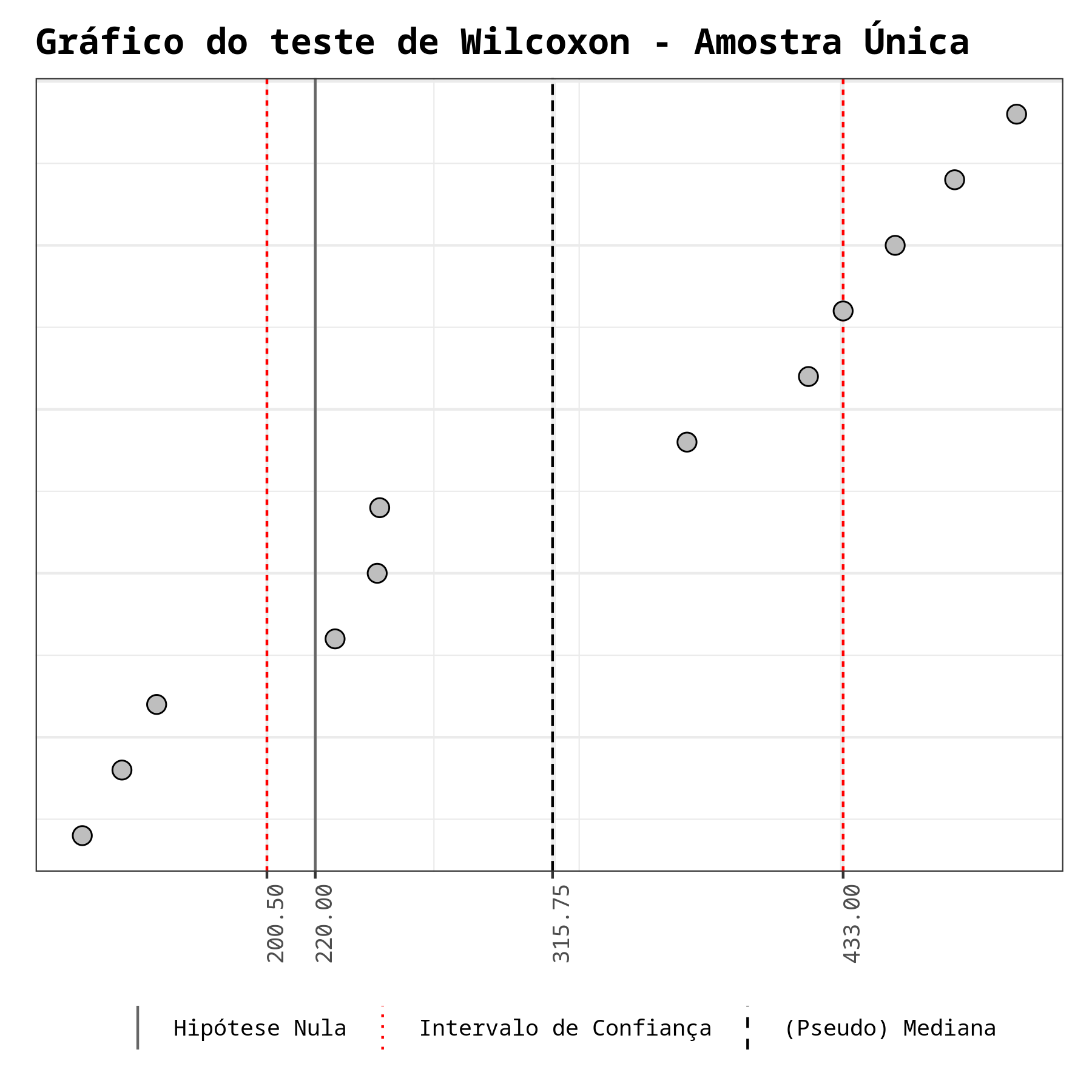
A estatística do teste é V = 63. Como o p-valor é igual a 0,0639 = 6,39% > 5% não rejeitamos a hipótese nula de que $\theta_0$ = 220 ao nível de significância de 5%.
Exemplo 2:
Duas amostras forneceram os seguintes valores de certa variável.
| Amostras | Dados |
|---|---|
| Amostra 1 | 29 |
| Amostra 1 | 39 |
| Amostra 1 | 60 |
| Amostra 1 | 78 |
| Amostra 1 | 82 |
| Amostra 1 | 112 |
| Amostra 1 | 125 |
| Amostra 1 | 170 |
| Amostra 1 | 192 |
| Amostra 1 | 224 |
| Amostra 1 | 263 |
| Amostra 1 | 275 |
| Amostra 1 | 276 |
| Amostra 1 | 286 |
| Amostra 1 | 369 |
| Amostra 1 | 756 |
| Amostra 2 | 126 |
| Amostra 2 | 142 |
| Amostra 2 | 156 |
| Amostra 2 | 228 |
| Amostra 2 | 245 |
| Amostra 2 | 246 |
| Amostra 2 | 370 |
| Amostra 2 | 419 |
| Amostra 2 | 433 |
| Amostra 2 | 454 |
| Amostra 2 | 478 |
| Amostra 2 | 503 |
Faremos o upload dos dados no sistema.
O teste de Wilcoxon será conduzido utilizando as configurações apresentadas na figura abaixo.
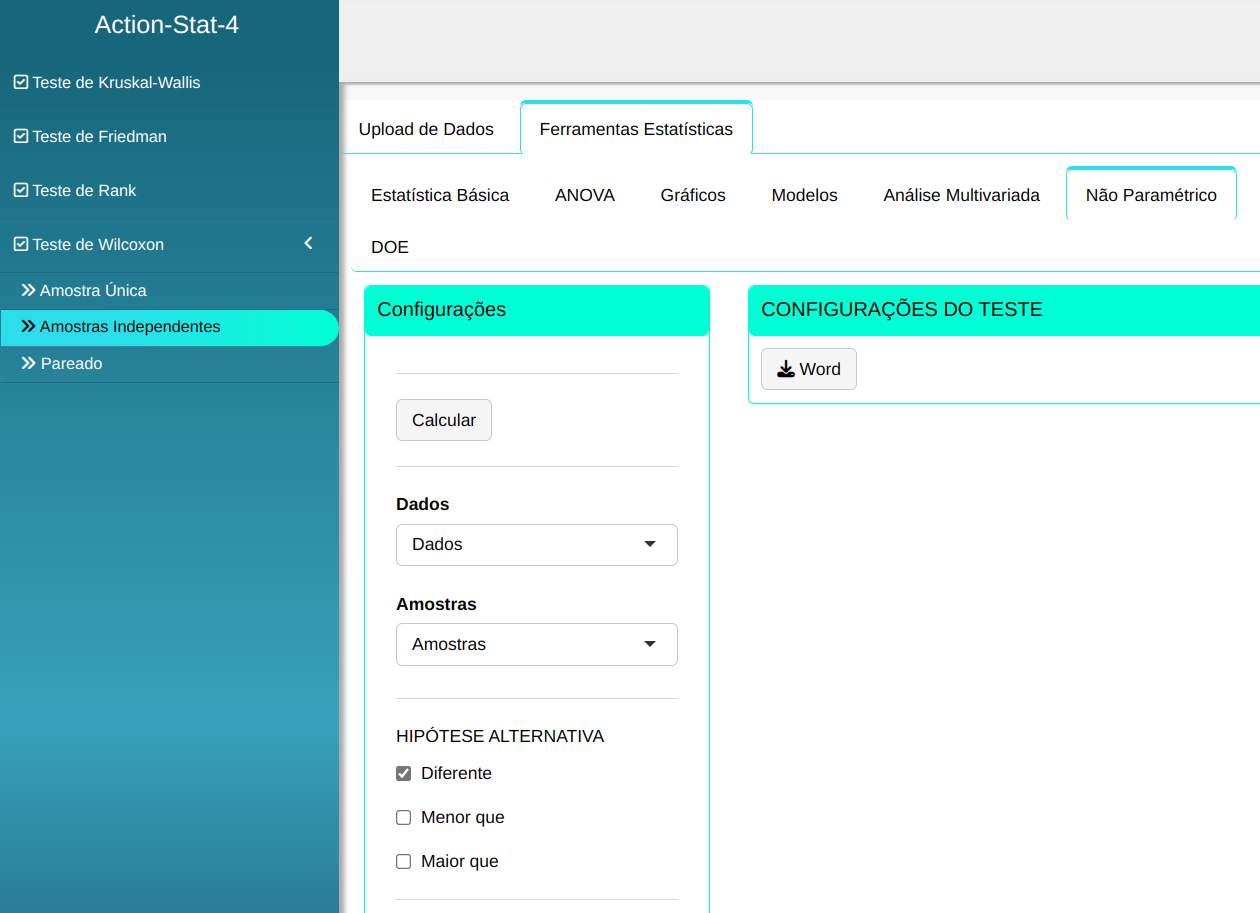
Clicando em Calcular obtemos os resultados e também é possível gerar a análise e baixar em formato Word.

Os resultados são:
Tabela da Estatística do Teste (Wilcoxon)
| Valores | |
|---|---|
| Estatística | 141 |
| P-valor | 0.0373 |
| Hipótese Nula | 0 |
| Limite Inferior | 4 |
| (Pseudo) Mediana | 133.5 |
| Limite Superior | 240 |
| Nível de Confiança | 0.95 |
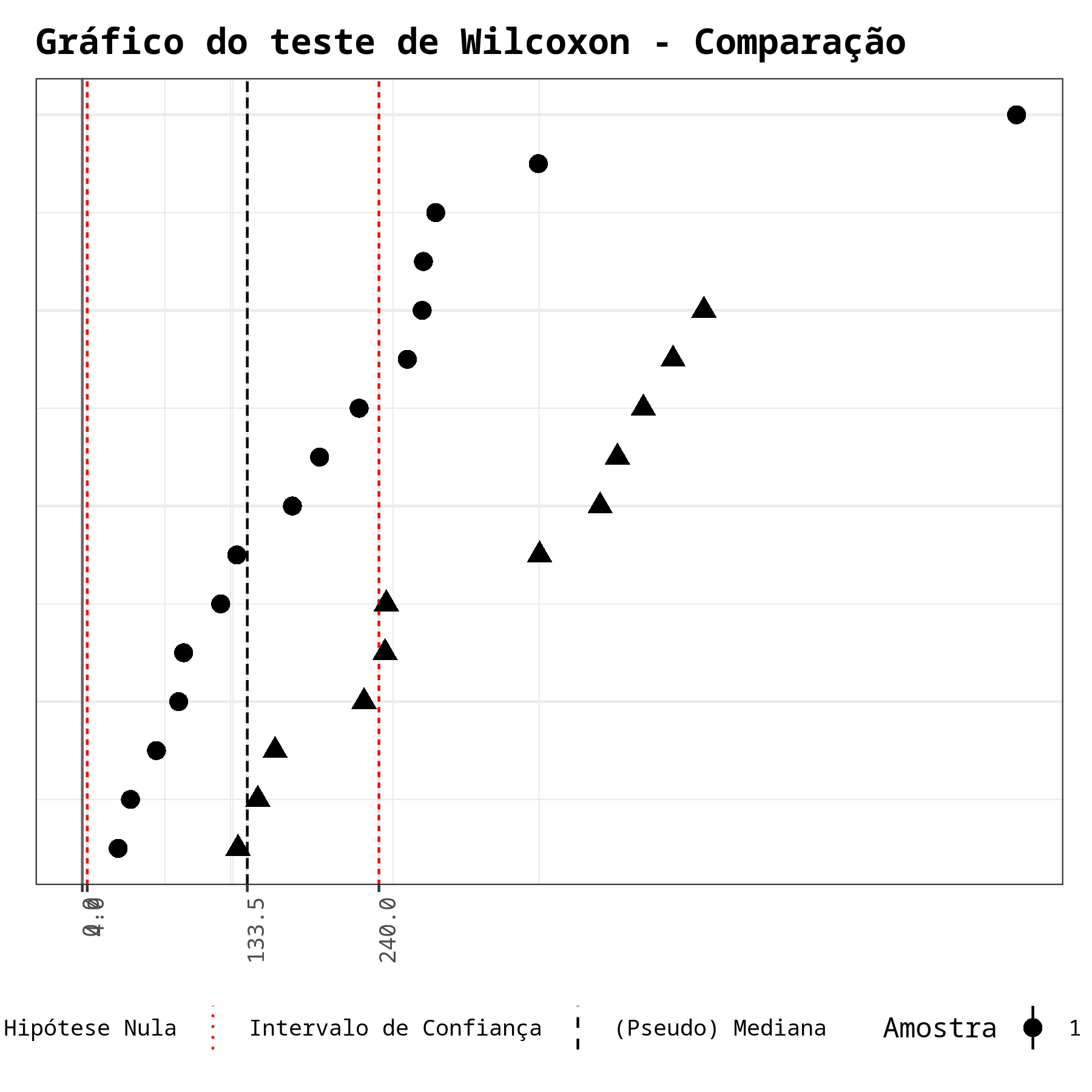
A estatística do teste é W = 141. Como o p-valor é igual a 0,0373 = 3,73% < 5%. rejeitamos a hipótese nula. Assim, temos evidências de que as amostras vem de populações que possuem medianas diferentes.
Exemplo 3:
Consideremos duas amostras dependentes cujos dados estão na tabela. Existem evidências de diferença entre as duas amostras?
| Amostra 1 | Amostra 2 |
|---|---|
| 564 | 557 |
| 521 | 505 |
| 495 | 465 |
| 564 | 562 |
| 560 | 545 |
| 481 | 448 |
| 545 | 531 |
| 478 | 458 |
| 580 | 562 |
| 484 | 485 |
| 539 | 520 |
| 467 | 445 |
Faremos o upload dos dados no sistema.
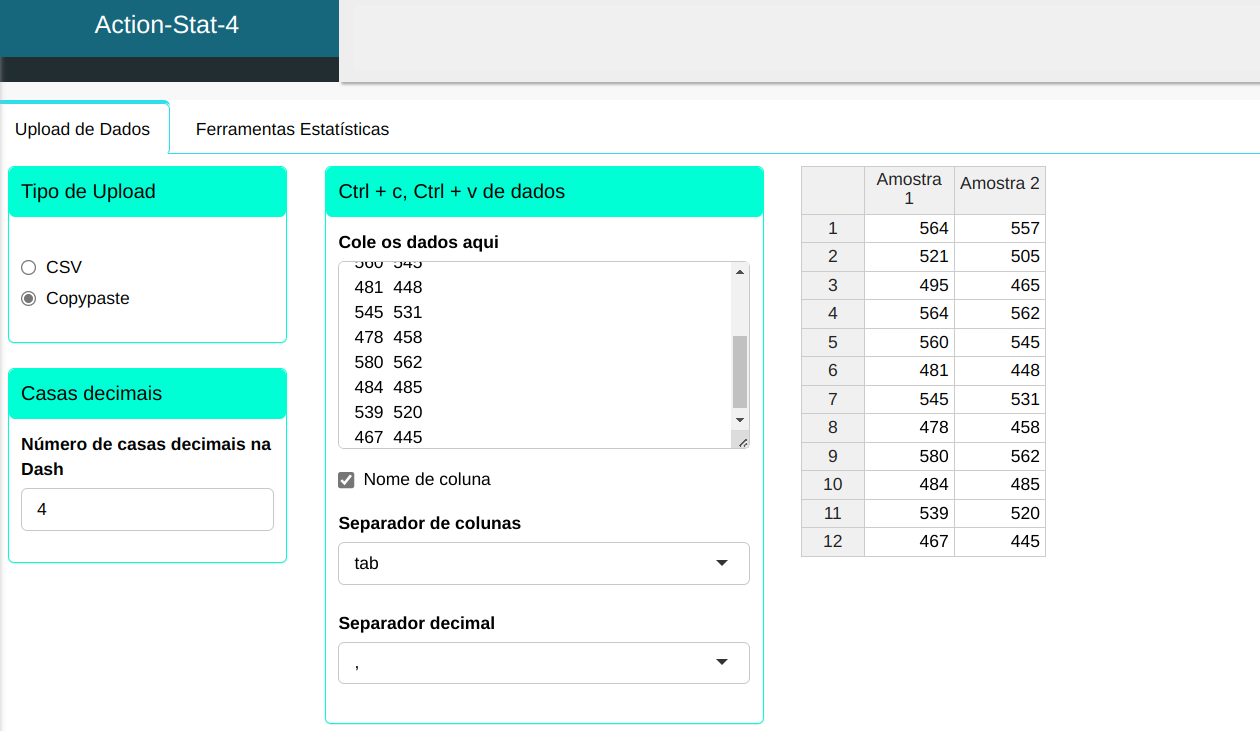
O teste de Wilcoxon será conduzido utilizando as configurações apresentadas na figura abaixo.
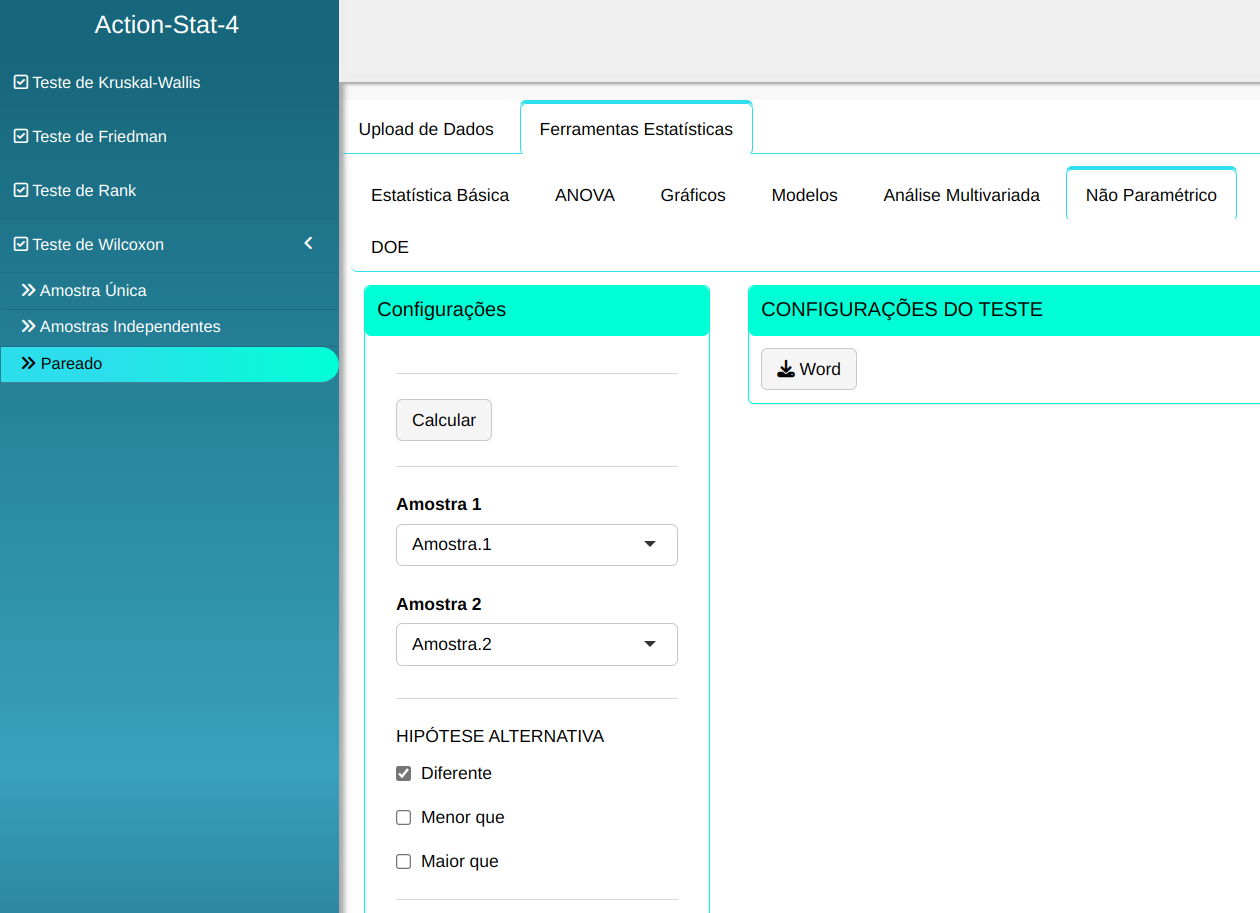
Clicando em Calcular obtemos os resultados e também é possível gerar a análise e baixar em formato Word.

Os resultados são:
Tabela da Estatística do Teste (Wilcoxon)
| Valores | |
|---|---|
| Estatística | 77 |
| P-valor | 0.001 |
| Hipótese Nula | 0 |
| Limite Inferior | 9 |
| (Pseudo) Mediana | 16.75 |
| Limite Superior | 23.5 |
| Nível de Confiança | 0.95 |
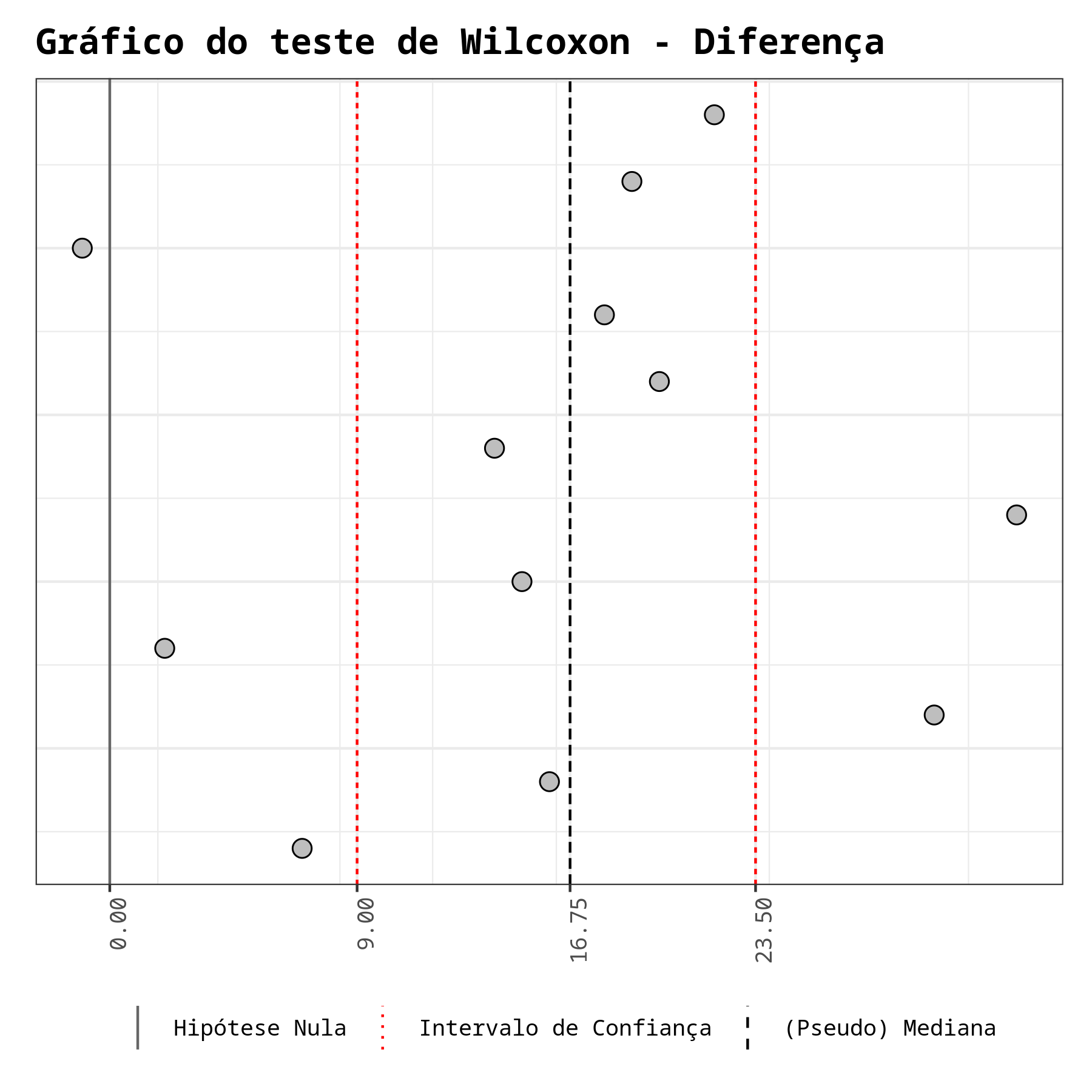
A estatística do teste é W = 77. Como o P-valor = 0,000976563 < 5% então, ao nível de significância de 5% existem evidências de diferença entre as duas amostras.