1. Análise Gráfica

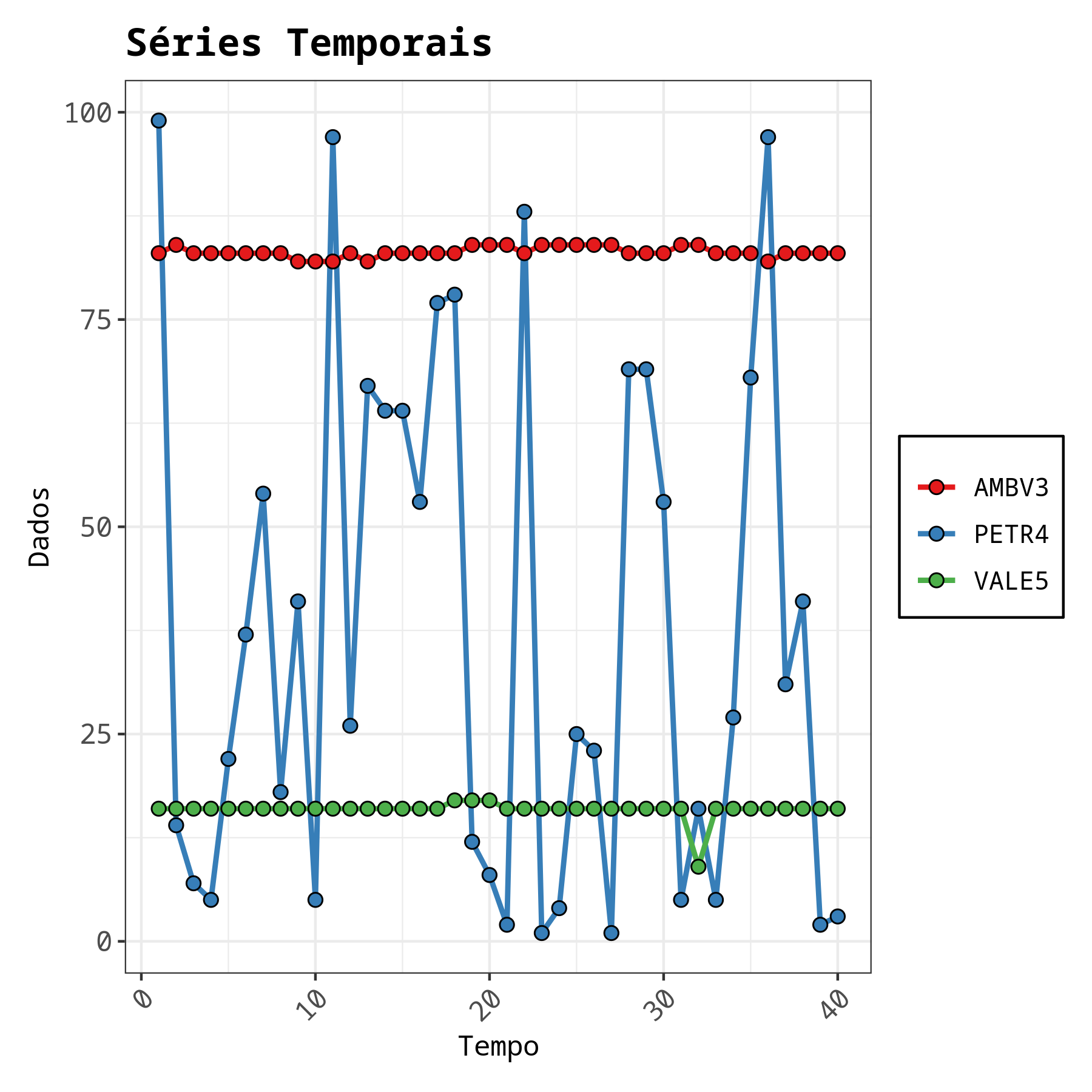
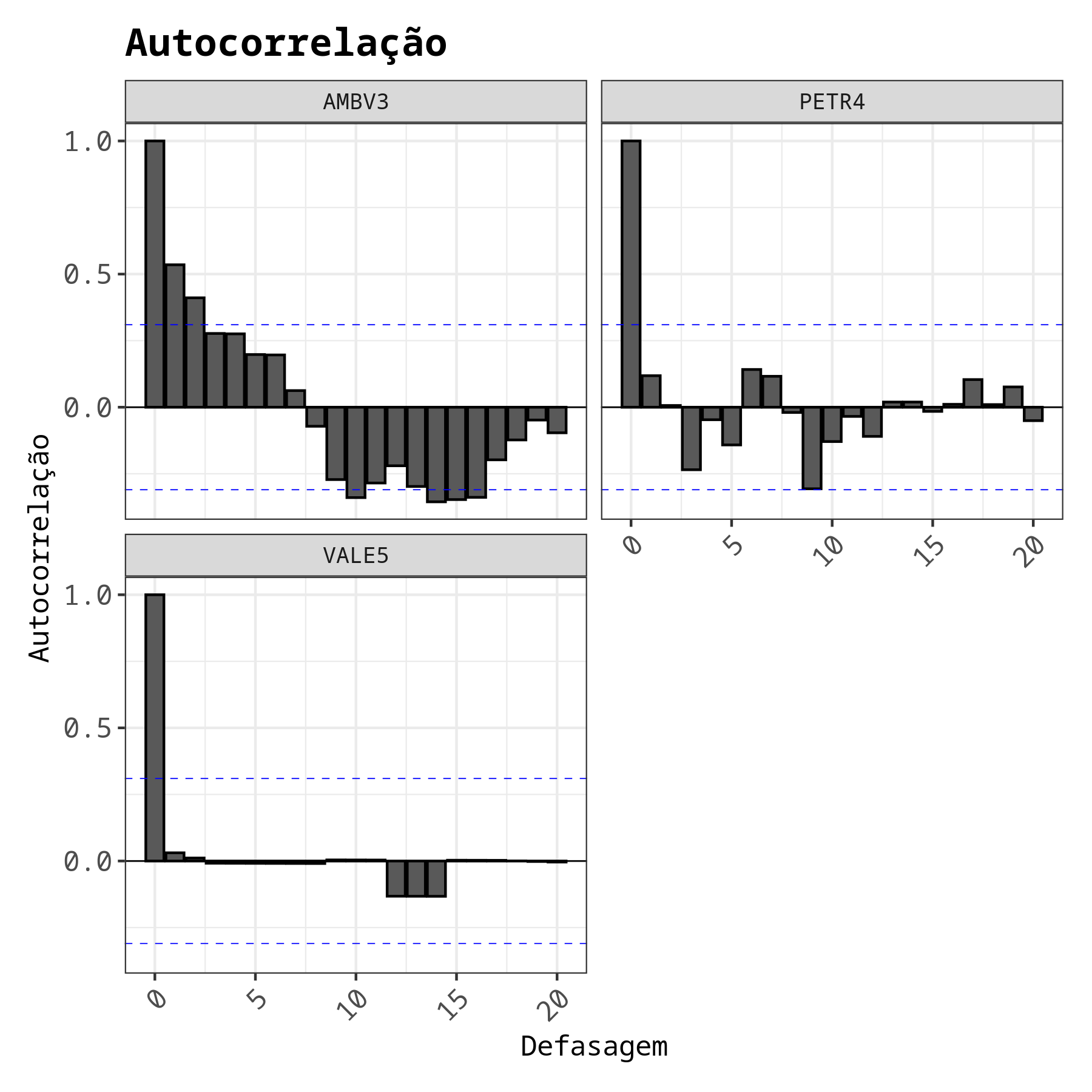
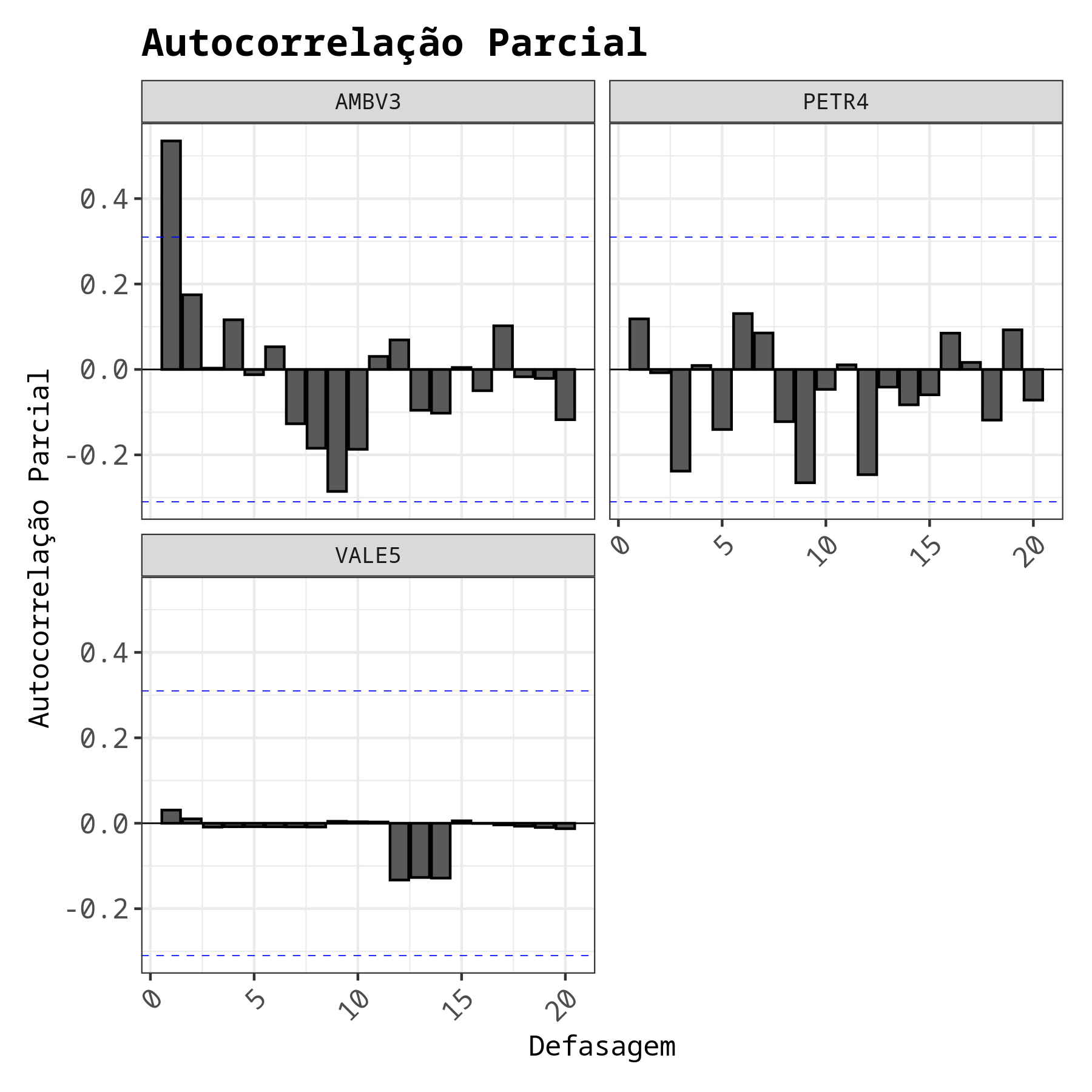
Frequentemente temos que lidar com experimentos que evoluem no tempo. Para o melhor entendimento destes tipos de experimentos, a análise gráfica é uma ferramenta essencial. Na análise gráfica é possível visualizar os gráficos da série temporal, da função de auto-correlação, da função de auto-correlação parcial e da covariância. Com o gráfico da série temporal é possível identificar de forma subjetiva se os dados apresentam algum comportamento especial, como, por exemplo tendência ou sazonalidade. Já os gráficos da FAC e da FACP auxiliam na identificação de possíveis modelos para o ajuste dos dados.

Exemplo:

Análise gráfica dos ativos financeiros AMBV3, PETR4 e VALE5.

AMBV3	PETR4	VALE5
83	99	16
84	14	16
83	7	16
83	5	16
83	22	16
83	37	16
83	54	16
83	18	16
82	41	16
82	5	16
82	97	16
83	26	16
82	67	16
83	64	16
83	64	16
83	53	16
83	77	16
83	78	17
84	12	17
84	8	17
84	2	16
83	88	16
84	1	16
84	4	16
84	25	16
84	23	16
84	1	16
83	69	16
83	69	16
83	53	16
84	5	16
84	16	9
83	5	16
83	27	16
83	68	16
82	97	16
83	31	16
83	41	16
83	2	16
83	3	16

---

Faremos o Upload dos dados no sistema.

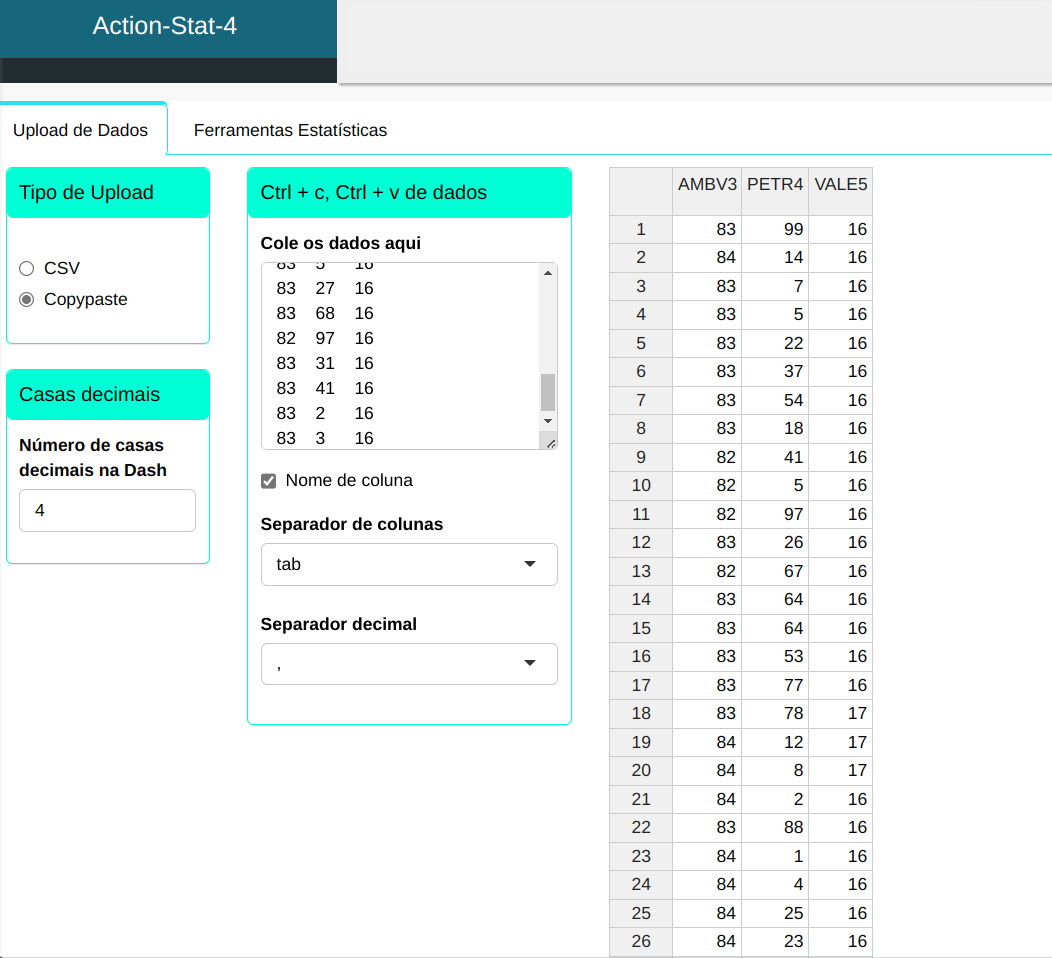
A análise gráfica será realizada conforme a configuração apresentada na figura abaixo.

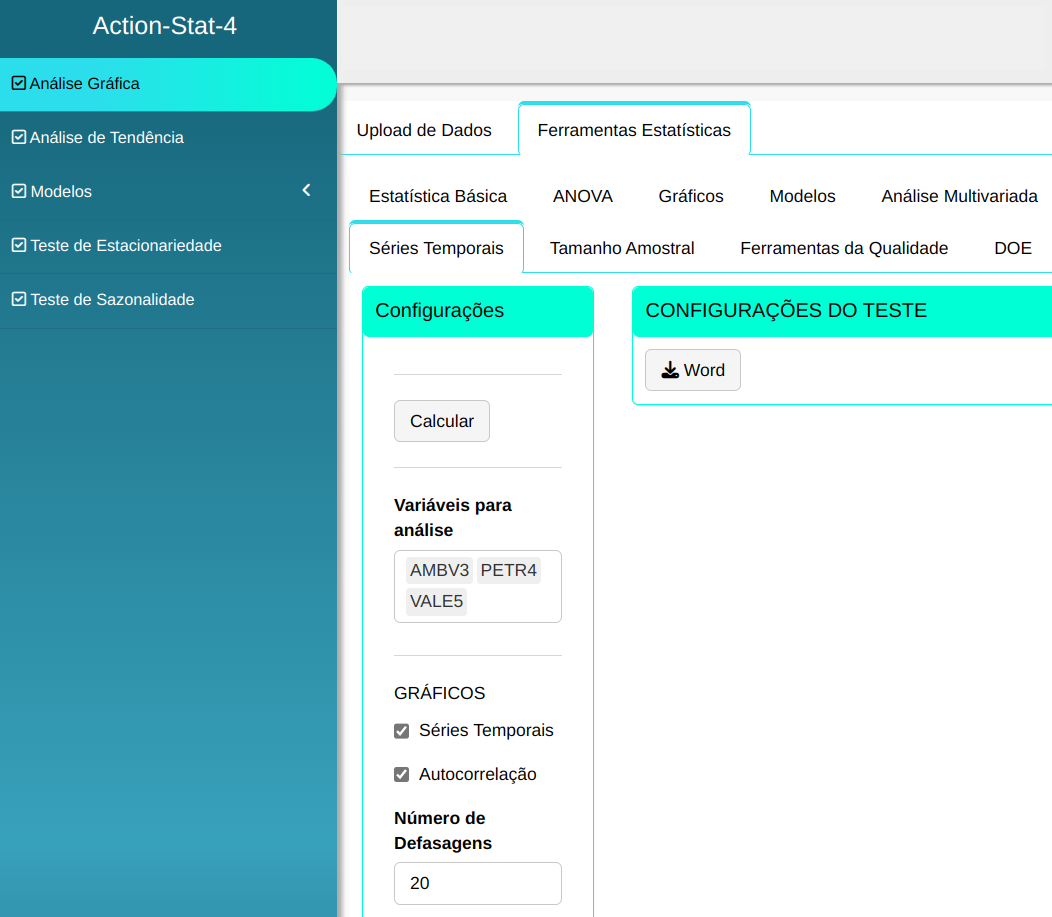
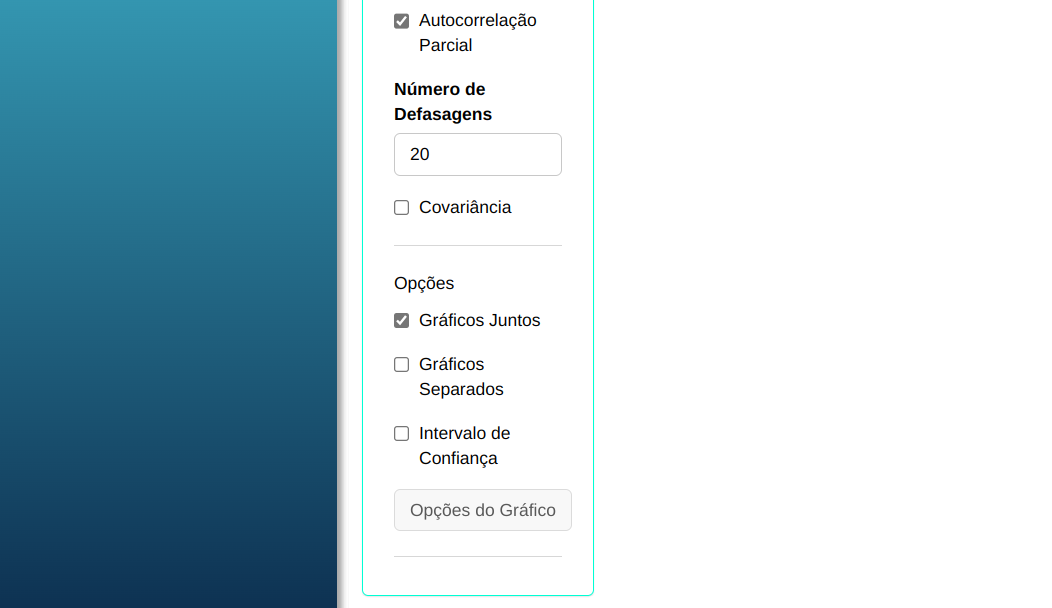
Em seguida, clique em Calcular para obter os resultados e também pode descarregá-las em formato Word.

Os resultados são: