4. Testes de Estacionariedade

Quase a totalidade dos modelos propostos para séries temporais, apresentam como suposição a estacionariedade. Assim, uma questão fundamental é saber quando que uma série temporal é estacionária. Na ferramenta Testes de Estacionariedade três testes estão disponíveis para verificar a estacionariedade da série.

Exemplo:

Realizaremos o teste para os seguintes dados:

AMBV3
84,06
83,85
83,56
83,47
83,27
82,81
82,2
82,06
81,62
80,77
81,3
81,92
82,75
82,77
82,84
82,82
82,72
82,29
81,18
80,11
80,27
80,21
79,92
79,96
80,19
80,17
80,17
79,85
81
80,44
79,96
79,85
79,82
80,11
80,2
80,31
81,18
80,81
81,15
81,32
81,21
81,4
81,1
81,4
82,27
82,15
81,78
81,69
81,34
81,88

---

Realizaremos o upload dos dados no sistema

O teste será realizado conforme a configuração apresentada na figura abaixo

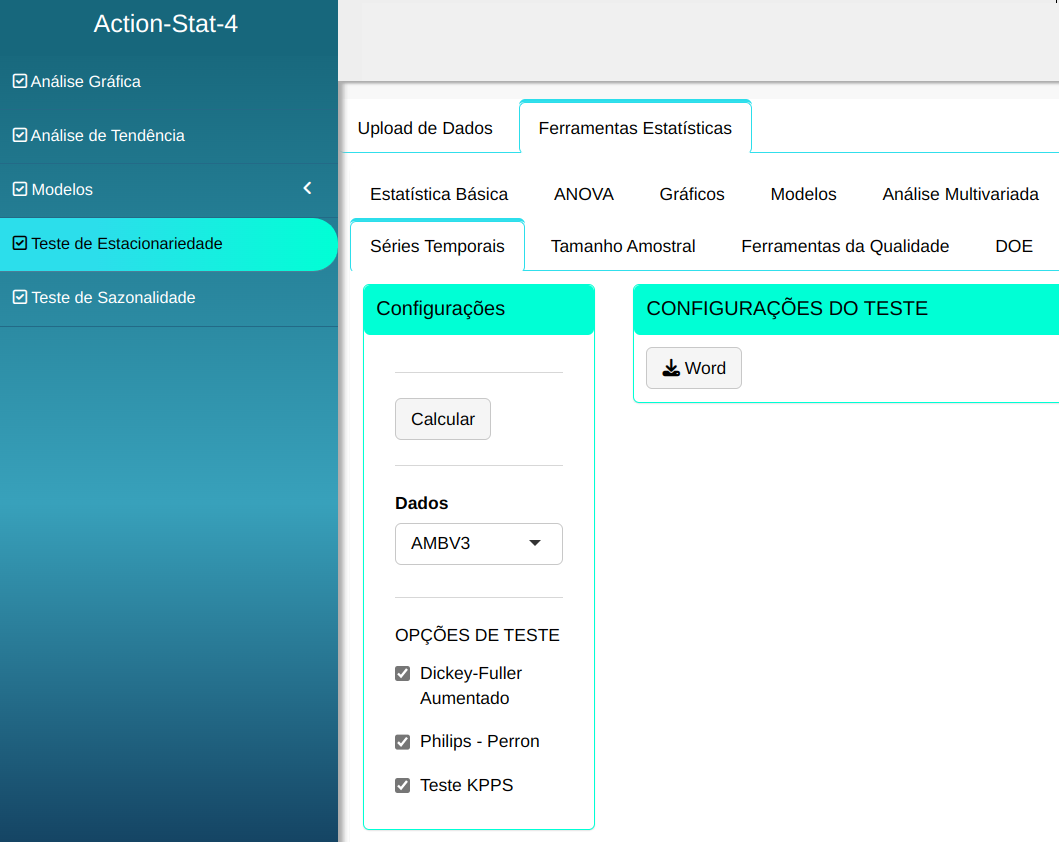
Clique em Calcular para obter os resultados e baixá-los em formato Word.

Os resultados são:

Teste de Dickey-Fuller Aumentado

	Dickey-Fuller
Estatística	-1.90501089436462
P-Valor	0.612390335192691
Tamanho da Amostra	50
Hipótese Nula	Existe pelo menos uma raiz unitária
Hipótese Alternativa	Não existe raiz unitária

---

Teste de Phillips-Perron

	Dickey-Fuller Z(alpha)
Estatística	-6.09026378709285
P-Valor	0.753893665311693
Tamanho da Amostra	50
Hipótese Nula	Existe pelo menos uma raiz unitária
Hipótese Alternativa	Não existe raiz unitária

---

Teste KPSS

	KPSS Level
Estatística	0.540460035842587
P-Valor	0.0325540459813994
Tamanho da Amostra	50
Hipótese Nula	A série temporal é estácionaria
Hipótese Alternativa	A série temporal apresenta raiz

---