5. Testes de Sazonalidade

Algumas séries temporais apresentam um comportamento conhecido como sazonalidade. A sazonalidade de uma série temporal é o número de observações que a série leva para repetir o padrão. Na ferramenta Testes de Sazonalidade, é possível realizar dois testes para verificar se a série apresenta sazonalidade.

Exemplo:

Realizaremos o teste com o seguinte conjunto de dados:

AMBV3
84,06
83,85
83,56
83,47
83,27
82,81
82,20
82,06
81,62
80,77
81,30
81,92
82,75
82,77
82,84
82,82
82,72
82,29
81,18
80,11
80,27
80,21
79,92
79,96
80,19
80,17
80,17
79,85
81,00
80,44
79,96
79,85
79,82
80,11
80,20
80,31
81,18
80,81
81,15
81,32
81,21
81,40
81,10
81,40
82,27
82,15
81,78
81,69
81,34
81,88

---

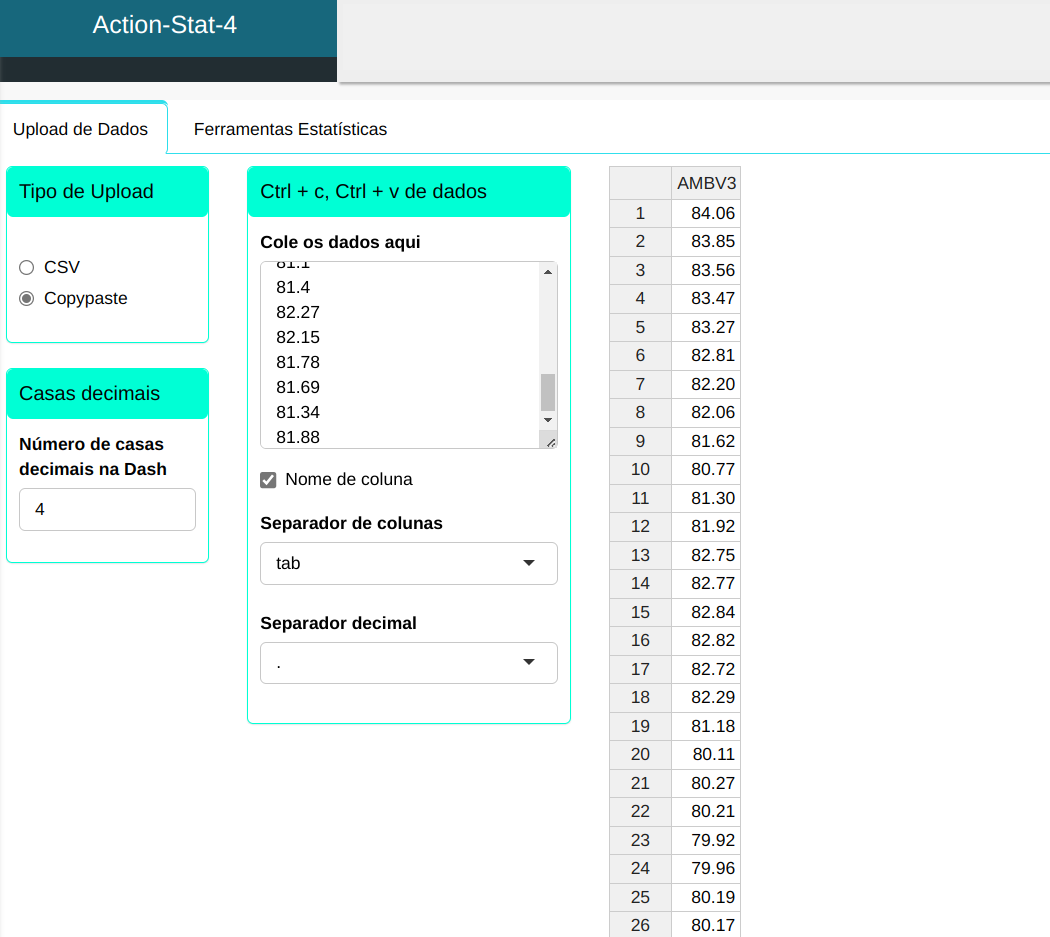
Faremos o upload dos dados no sistema.

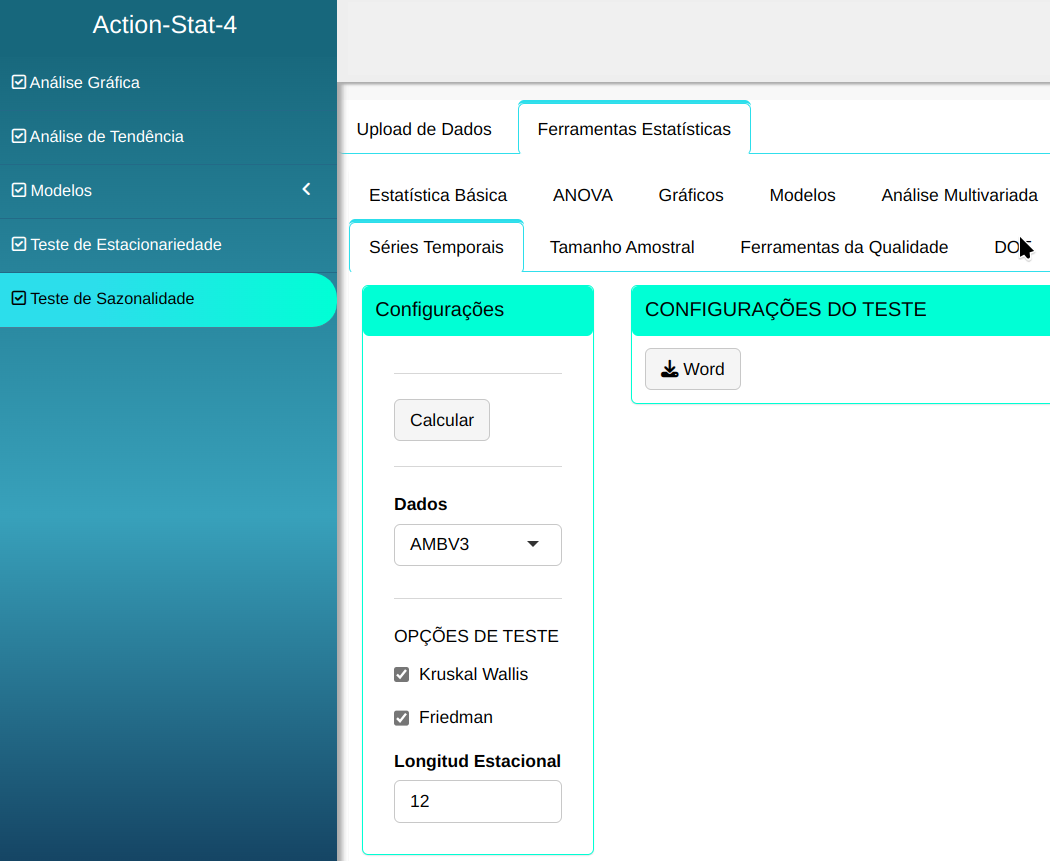
O Testes é elaborado, conforme a configuração apresentada na figura abaixo.

Em seguida, clique em Calcular para obter os resultados e também pode descarregá-las em formato Word.

Os resultados são:

Teste de Kruskal-Wallis

	Kruskal-Wallis chi-squared
Estatística	28.0688775510204
P-Valor	0.003159616205745
Tamanho da Amostra	50
Longitud Estacional	12
Hipótese Nula	Não há sazonalidade determinística
Hipótese Alternativa	Há sazonalidade determinística

---

Teste de Friedman

	Friedman chi-squared
Estatística	24.6153846153846
P-Valor	0.0103740819044975
Tamanho da Amostra	50
Longitud Estacional	12
Hipótese Nula	Não há sazonalidade determinística
Hipótese Alternativa	Há sazonalidade determinística

---