2. Intervalo de Confiança
A partir dos dados do intervalo de confiança é possível obter o tamanho amostral da população para a média e para a proporção.
Exemplo 1:
Suponha que uma pequena amostra piloto de n=10, extraída de uma população, forneceu os valores $\overline{x}$=15 e $s^2$ =16. Qual o tamanho amostral necessário para estimar a média populacional $\mu$ com erro amostral de no máximo 0,5 e com nível de confiança 1- $\alpha$ =0,95?
Então calcularemos o tamanho da amostra considerando os seguintes valores
| Desvio padrão - s | Nível de significância | Erro máximo amostral |
| $\quad\qquad$ 4 | $\quad\qquad$ 0,05 | $\qquad\qquad$0,5 |
Para realizar a análise configuramos conforme a figura de abaixo com os dados da tabela.
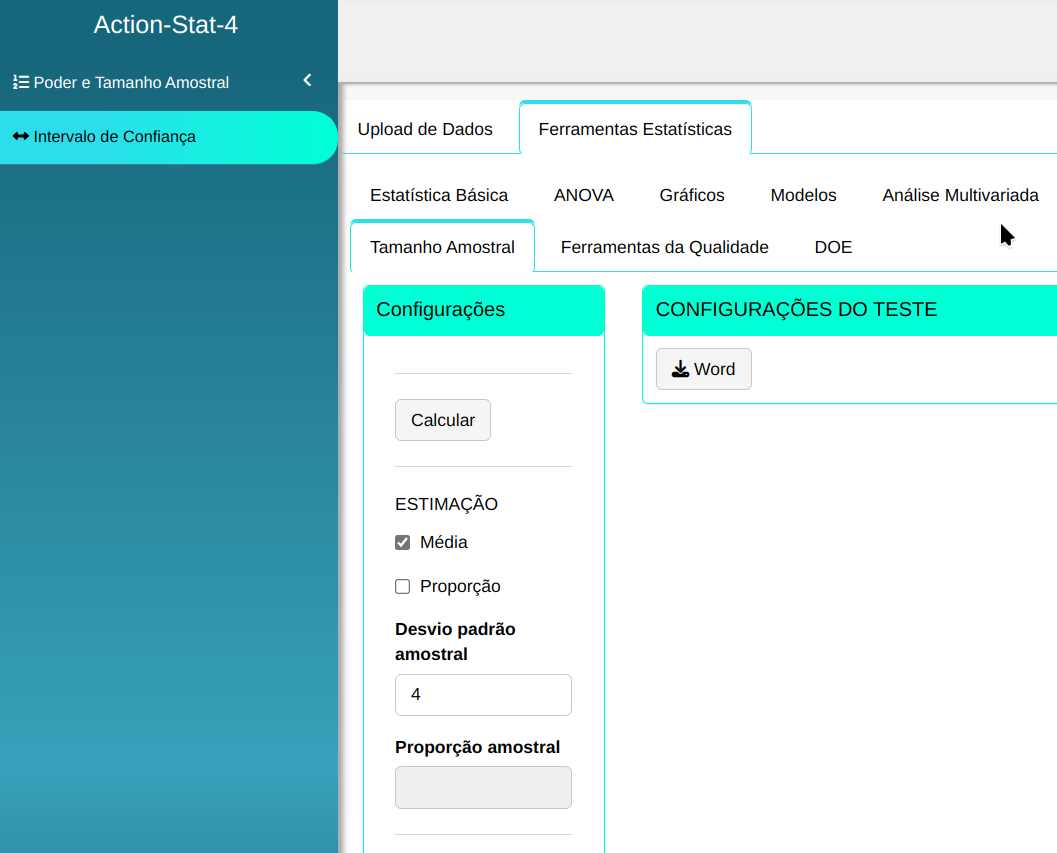
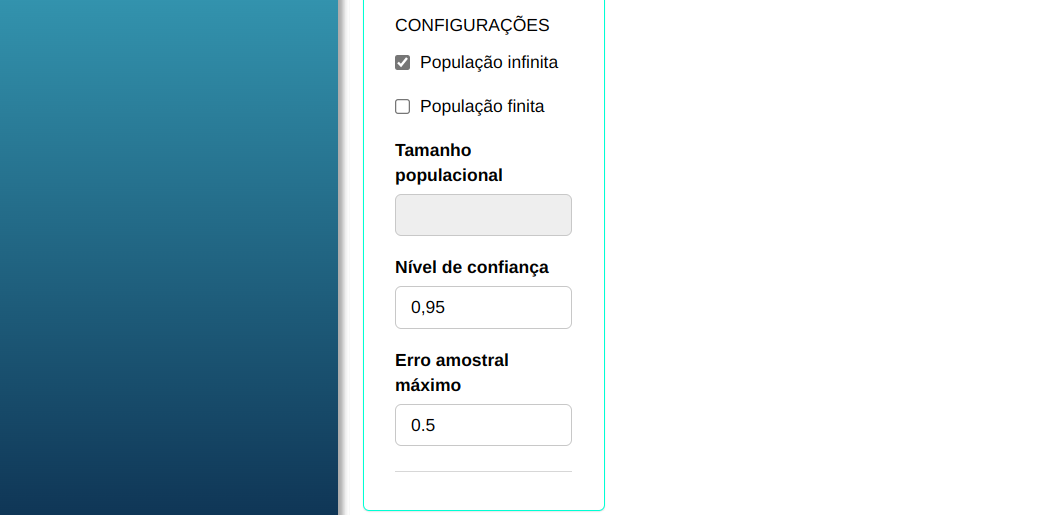
Em seguida, clique em Calcular para obter os resultados e também pode descarregá-los em formato Word.

Os resultados são:
Cálculo do Tamanho da Amostra
| tab | |
|---|---|
| Tamanho Amostral | 246 |
| Erro Amostral Máximo | 0.5 |
| Desvio-Padrão Amostral | 4 |
| Tamanho da População | Inf |
| Nível de Confiança | 0.95 |
Com isso concluímos que, o tamanho amostral necessário para estimar a média populacional com um erro amostral de no máximo 0,5 e um nível de confiança de 95%, é aproximadamente 246.
Exemplo 2:
Suponha que em uma pesquisa de mercado foi estimado que 60% das pessoas entrevistadas preferem a marcar A de um analgésico. Essa informação é baseada em pesquisas anteriores. Calcule o tamanho amostral para que o erro amostral de $\hat{p}$ seja menor que o erro de 0,03 e confiança 1- $\alpha$ = 95%.
Então calcularemos o tamanho da amostra considerando os seguintes valores
| Proporção amostral | Nível de significância | Erro máximo amostral |
| $\quad\qquad$ 0,6 | $\quad\qquad$ 0,05 | $\qquad\qquad$0,03 |
Para realizar a análise configuramos conforme a figura de abaixo com os dados da tabela.
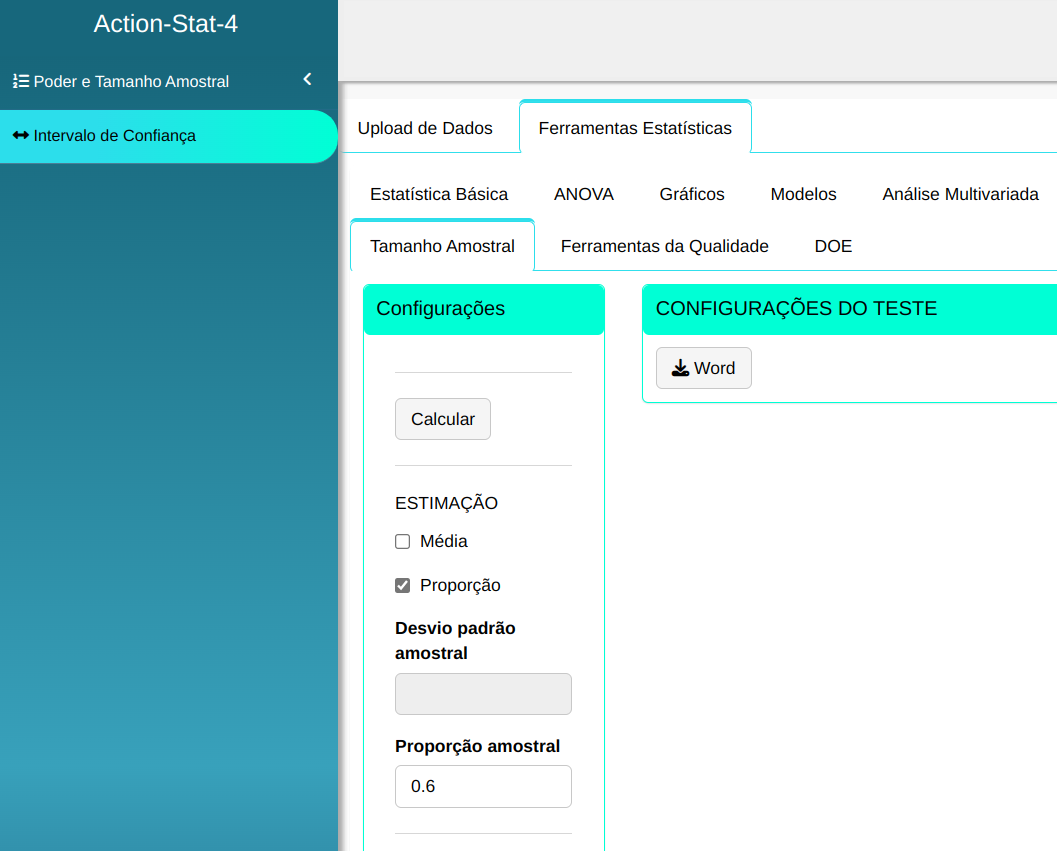
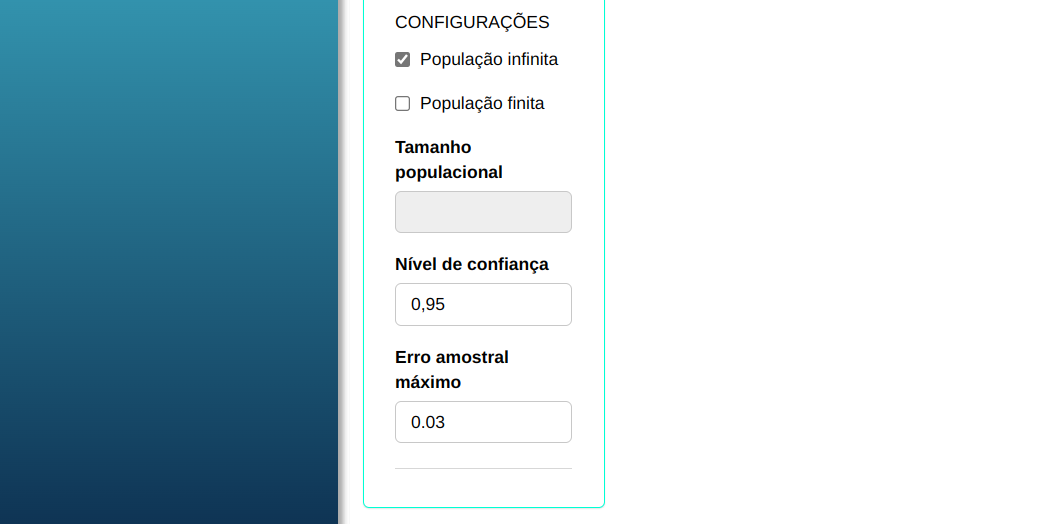
Clique em Calcular para visualizar os resultados e baixá-los em formato Word.

Os resultados são:
Cálculo do Tamanho da Amostra
| tab | |
|---|---|
| Tamanho Amostral | 1025 |
| Erro Amostral Máximo | 0.03 |
| Proporção Amostral | 0.6 |
| Tamanho da População | Inf |
| Nível de Confiança | 0.95 |
Com isso concluímos que, o tamanho amostral necessário para estimar a proporção populacional com um erro amostral de no máximo 0,03 e um nível de confiança de 95%, é aproximadamente 1025.