4. Anova
A ANOVA é um método utilizado para testar diferenças significativas entre as médias de grupos de dados. Ela é frequentemente aplicada em pesquisas experimentais para comparar os efeitos de diferentes tratamentos. O teste calcula a estatística F, que corresponde à razão entre a variação entre os grupos e a variação dentro dos grupos.
Exemplo 1:
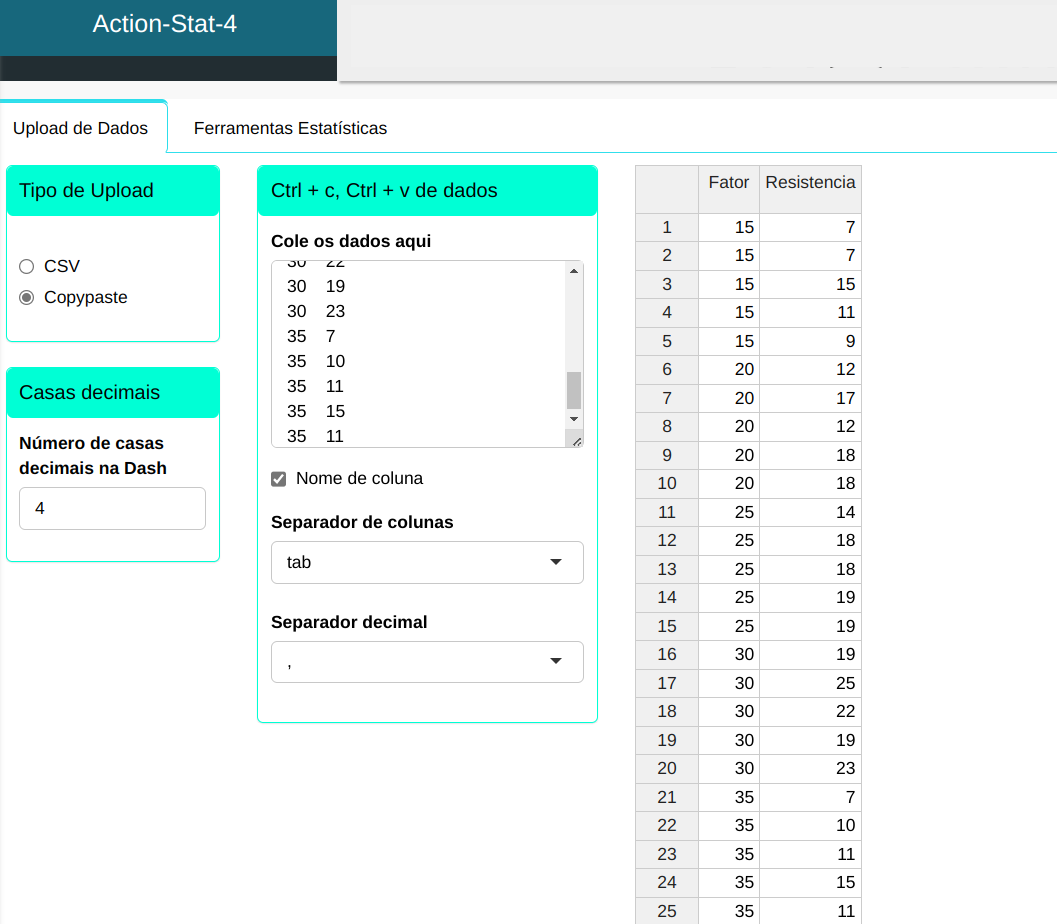
Considere o processo de produção de uma fibra sintética, onde o experimentador quer conhecer a influência da porcentagem de algodão na resistência da fibra. Para isto, foi realizado um experimento totalmente aleatorizado, onde diversos níveis de porcentagem de algodão foram avaliados com respeito à resistência da fibra. Um ponto importante na montagem do experimento é que para cada nível do fator (porcentagem de algodão), os outros fatores que influenciam o processo devém apresentar um padrão homogêneo de variabilidade. No experimento, tomamos 5 níveis para a porcentagem de algodão e 5 replicações. Os valores estão na tabela abaixo:
| Fator | Resistência |
|---|---|
| 15 | 7 |
| 15 | 7 |
| 15 | 1 |
| 15 | 11 |
| 15 | 9 |
| 20 | 12 |
| 20 | 17 |
| 20 | 12 |
| 20 | 18 |
| 20 | 18 |
| 25 | 14 |
| 25 | 18 |
| 25 | 18 |
| 25 | 19 |
| 25 | 19 |
| 30 | 19 |
| 30 | 25 |
| 30 | 22 |
| 30 | 19 |
| 30 | 23 |
| 35 | 7 |
| 35 | 10 |
| 35 | 11 |
| 35 | 15 |
| 35 | 11 |
| Número de níveis | Observação por nível | Desvio padrão |
| $\quad\qquad$ 5 | $\quad\qquad$ 5 | 5.151698749 |
Fazemos a análise e configuramos de acordo com a figura abaixo.
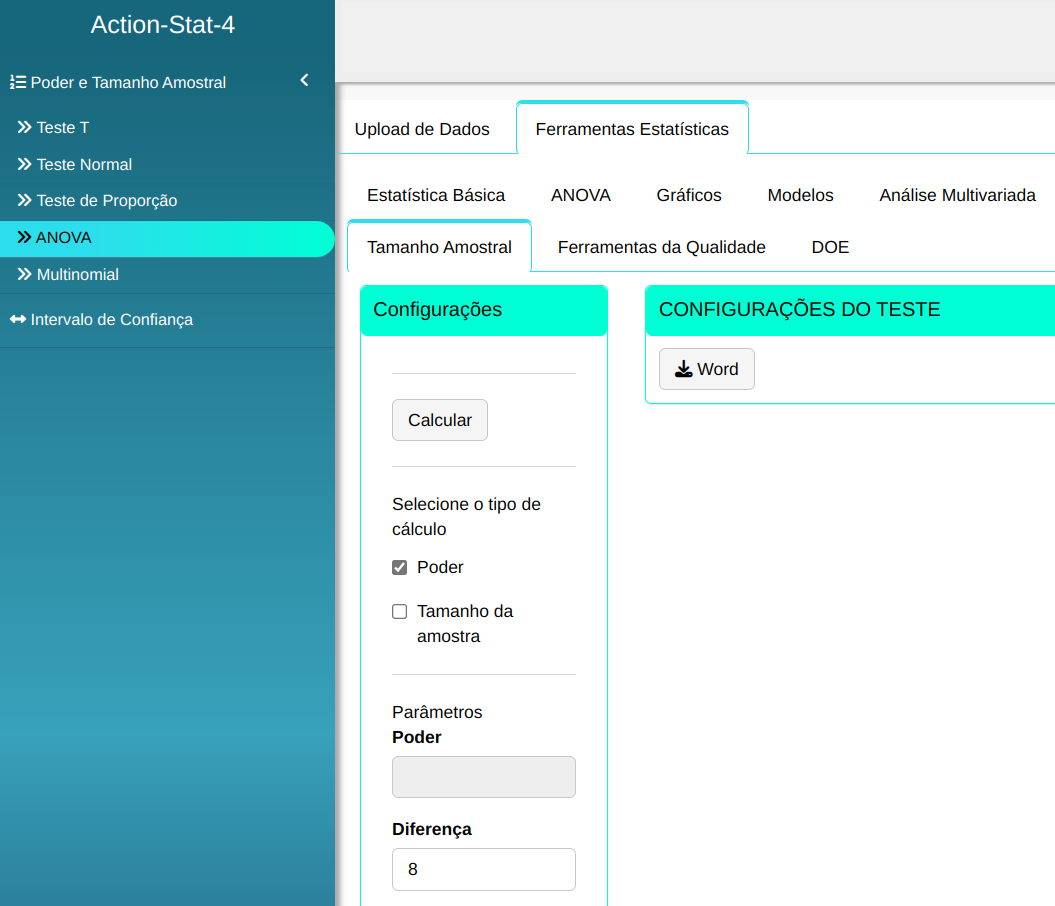
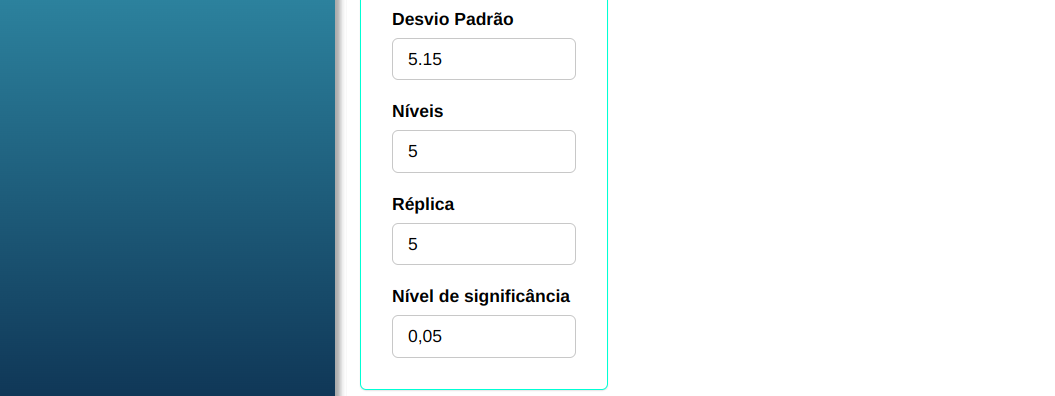
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.
Os resultados são:
Poder e Tamanho da amostra - ANOVA
| V1 | |
|---|---|
| Poder | 0.3812579 |
| Níveis | 5.0000000 |
| Réplica | 5.0000000 |
| Diferença | 8.0000000 |
| Desvio padrão | 5.1500000 |
| Nível de significância | 0.0500000 |
Então, concluímos que, para um nível de significância $\alpha$ = 0,05, o teste tem um poder de, aproximadamente, 38,1%.
Exemplo 2:
No exemplo anterior, calcule o número mínimo de réplicas para que o teste detecte uma diferença $\Delta$ = 8 com um poder de, no mínimo, 0,9.

Fazemos a análise e configuramos de acordo com a figura abaixo.
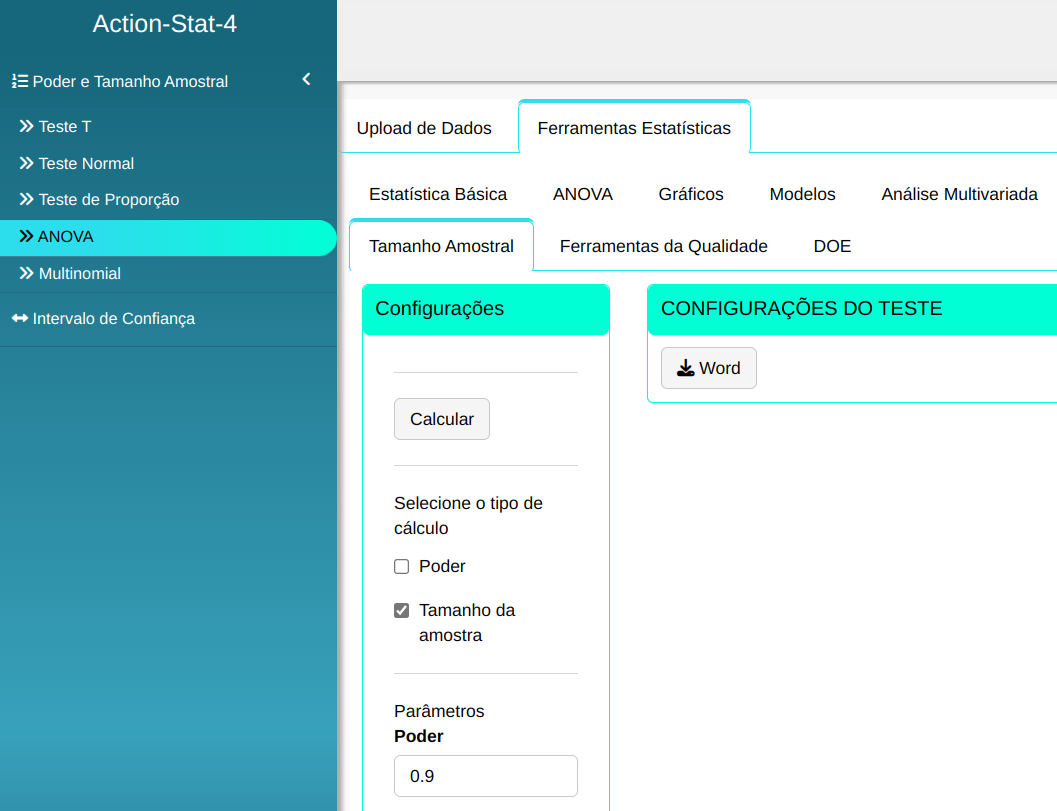
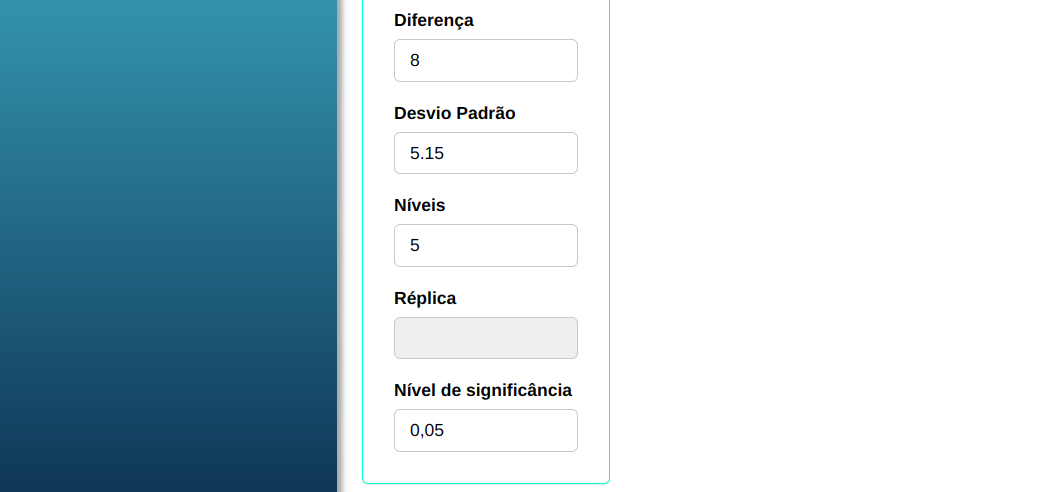
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.
Os resultados são:
Poder e Tamanho da amostra - ANOVA
| V1 | |
|---|---|
| Poder | 0.90 |
| Níveis | 5 |
| Réplica | 14 |
| Diferença | 8 |
| Desvio padrão | 5.15 |
| Nível de significância | 0.05 |
Então concluímos que são necessárias 14 réplicas para que o teste tenha um poder de 90%