5. Multinomial
Utilizando o teste Qui-Quadrado calculamos o poder do teste de hipóteses ou o tamanho da amostra necessário para ter um determinado poder para o teste.
Exemplo 1:
Um fabricante garante que 90% das peças que fornece à linha de produção de uma determinada fábrica concorda com as especificações exigidas. A análise de uma amostra de 200 peças revelou 25 defeituosas. A um nível de 5%, calcule o poder do teste em detectar a diferença entre a proporção nula de 0,9 e uma, possível proporção real de 0,8.
Usaremos os dados da tabela abaixo
| n | $\mathbf{p_0}$ | $\mathbf{p_1}$ | $\mathbf{\alpha}$ |
| 200 | (0,9;0,1) | (0,8;0,2) | 0,05 |
| p0 | p1 |
|---|---|
| 0,9 | 0,8 |
| 0,1 | 0,2 |
Os dados serão carregados no sistema.
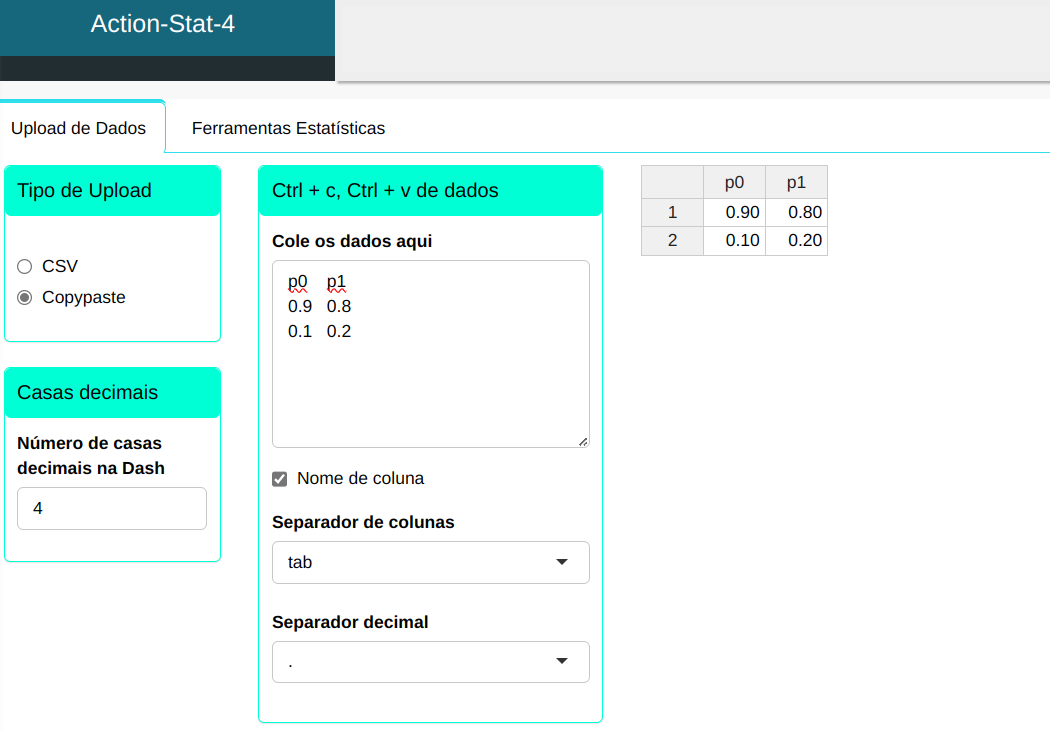
Para realizar a análise, conforme a configuração apresentada na figura a seguir.
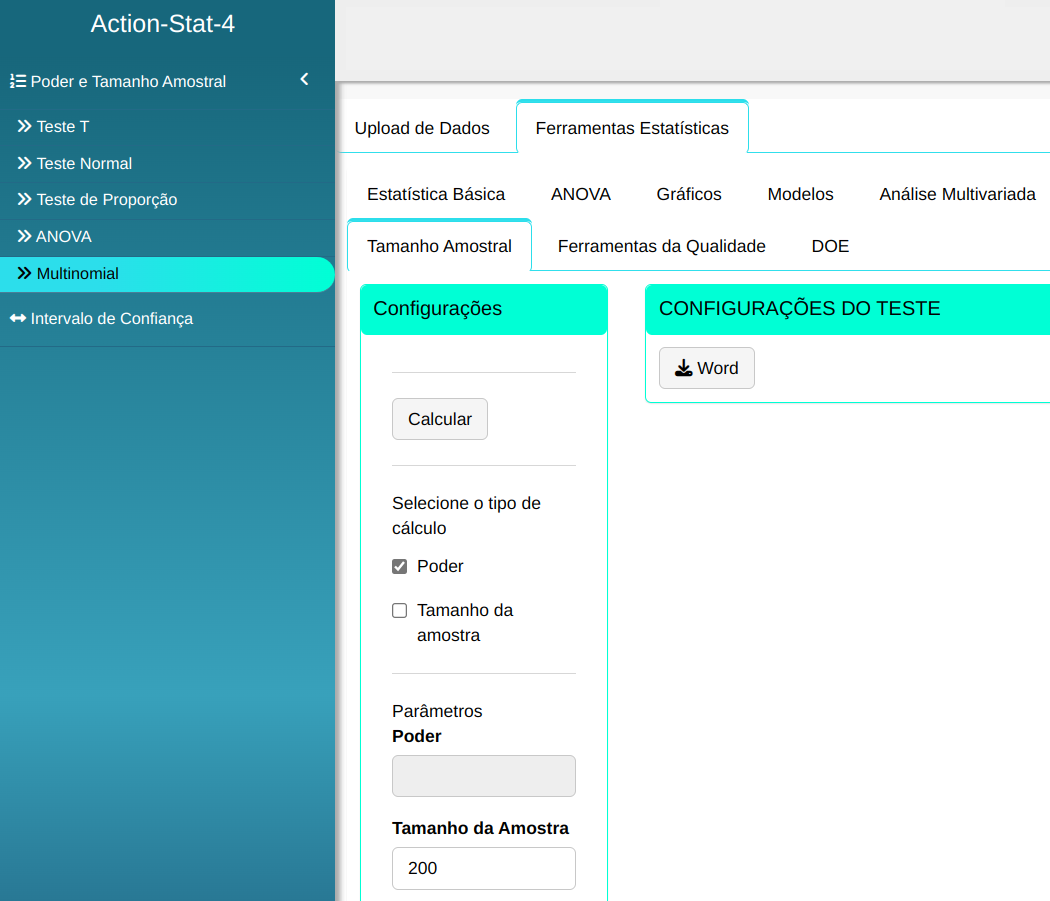
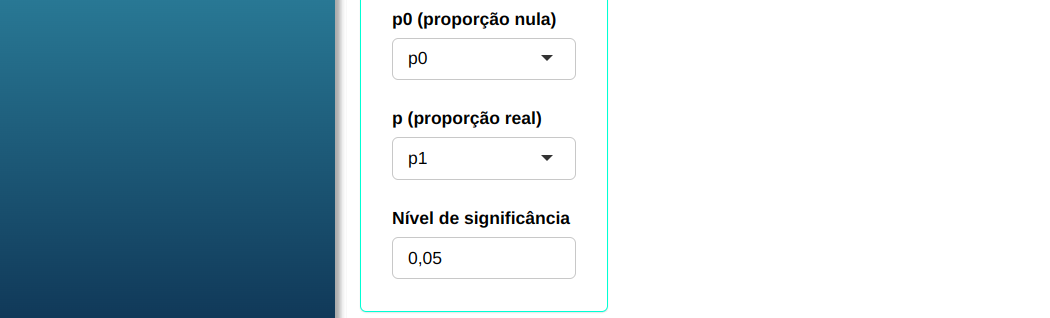
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e baixá-las em formato Word.

Os resultados são:
Resultado da análise
| Aviso | |
| Poder | 0.9970571 |
| Tamanho da amostra | 200 |
| p0 | 0.9 0.1 |
| p | 0.8 0.2 |
| Nível de significância | 0.05 |
Com isso, concluímos que o poder do teste em detectar a diferença entre a proporção nula de 0,9 e uma, possível proporção real de 0,8 é de aproximadamente 99,71%.
Exemplo 2:
A um nível de significância de 5%, calcule o tamanho amostral necessário para o teste de hipóteses detectar com um poder de, no mínimo 0,9, uma diferença entre a proporção da hipótese nula $p_0$ = 0,9 e uma, possível proporção real p = 0,87.
Usaremos os dados da tabela abaixo:
| $\mathbf{p_0}$ | $\mathbf{p_1}$ | $\mathbf{\alpha}$ | Poder |
| (0,9;0,1) | (0,87;0,13) | 0,05 | 0,9 |
| p0 | p1 |
|---|---|
| 0,90 | 0,87 |
| 0,10 | 0,13 |
Os dados serão carregados no sistema.
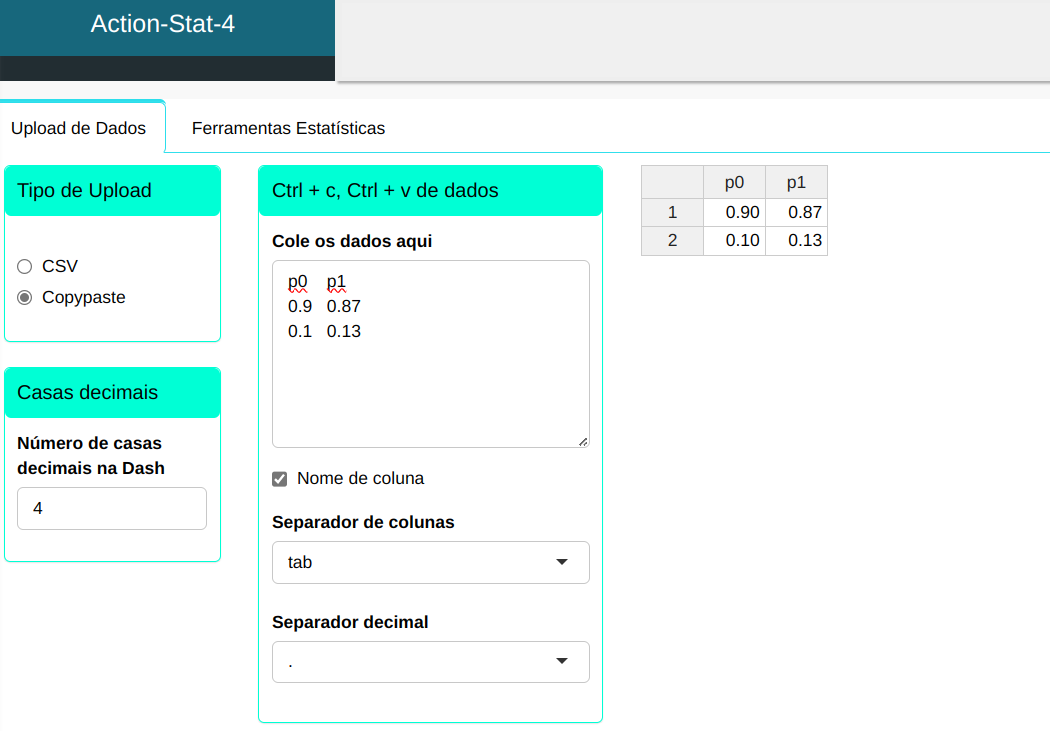
Para realizar a análise, conforme a configuração apresentada na figura a seguir.
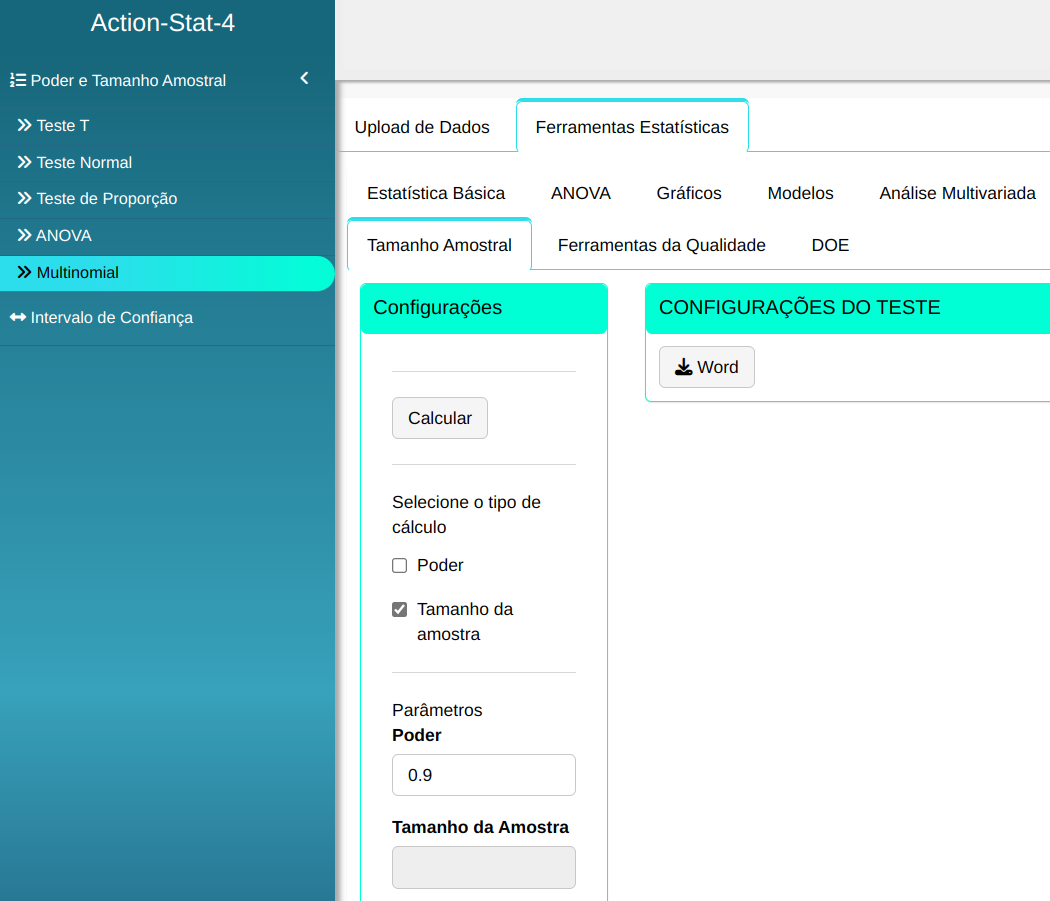
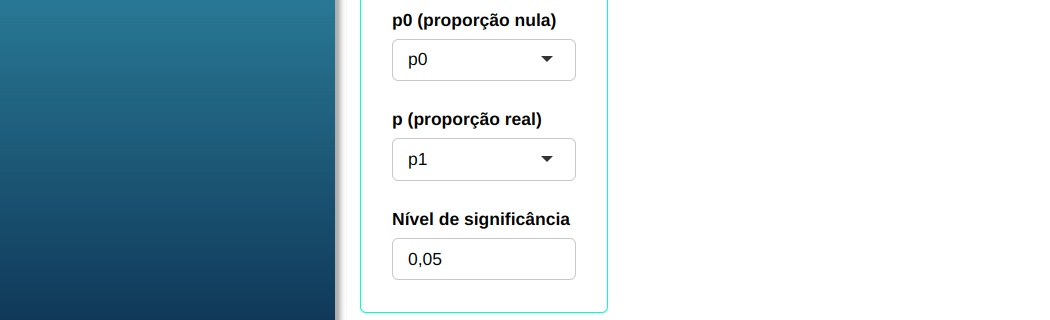
Em seguida, clique em Calcular para obter os resultados e tTambém pode descarregá-las em formato Word.

Os resultados são:
Resultado da análise
| Aviso | |
| Poder | 0.9 |
| Tamanho da amostra | 1051 |
| Proporção | 0.9 0.1 |
| Proporção hipotética | 0.87 0.13 |
| Nível de significância | 0.05 |
Concluímos então que, para que o teste detecte esta pequena diferença com poder de, no mínimo 0,9, é necessária uma amostra de tamanho 1051, no mínimo.