3. Teste de Proporção
Aqui o teste de uma proporção é utilizado para calcular o poder do teste ou o tamanho da amostra.
Exemplo 1:
Um fabricante garante que 90% das peças que fornece à linha de produção de uma determinada fábrica concorda com as especificações exigidas. A análise de uma amostra de 200 peças revelou 25 defeituosas. Calcule o poder do teste em se detectar a diferença entre a proporção $p_0$ = 0,9 da hipótese nula e uma proporção real $p$ = 0,8 a um nível de significância de 5%.
Usamos os dados da tabela abaixo:
| $\mathbf{n}$ | $\mathbf{\alpha}$ | $\mathbf{p}$ | $\mathbf{p_0}$ |
| 200 | 0,05 | 0,8 | 0,9 |
Fazemos a análise e configuramos conforme a figura de abaixo.
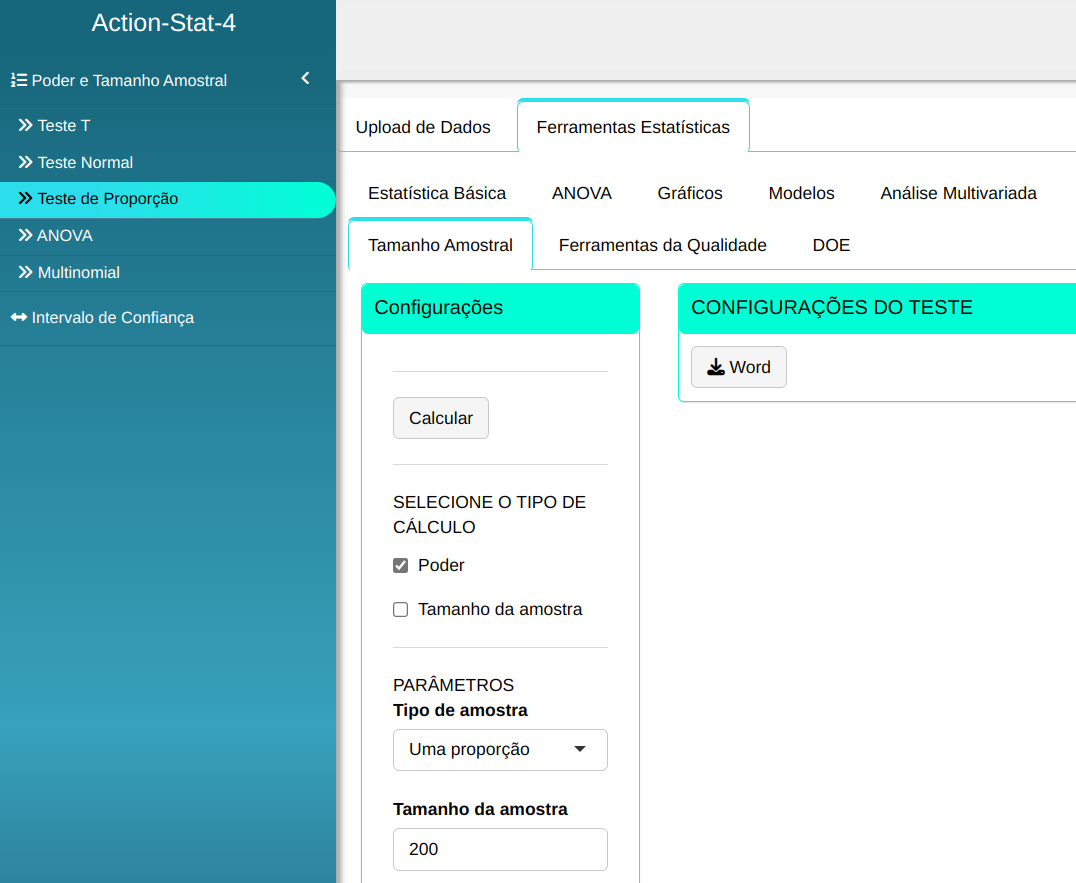
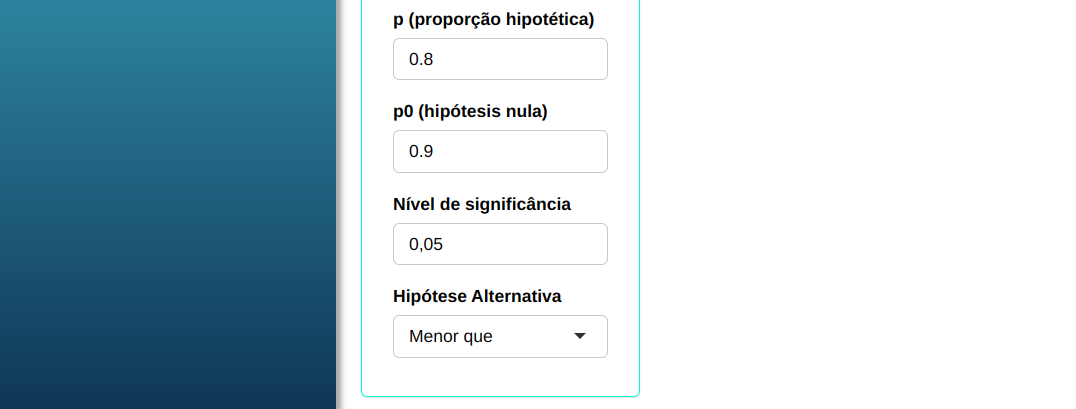
Em seguida, clique em Calcular para obter os resultados e também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Resultado da análise
| Aviso | |
| Poder | 0.9910723 |
| Tamanho da amostra | 200 |
| p | 0.8 |
| p0 | 0.9 |
| Nível de significância | 0.05 |
| Hipótese Alternativa | Menor que |
Com isso, concluímos que o teste tem poder de, aproximadamente 99,1% em detectar uma diferença entre a proporção da hipótese nula $p_0$ = 0,9 e uma possível proporção real $p$ = 0,8.
Exemplo 2:
Um fabricante garante que 90% das peças que fornece à linha de produção de uma determinada fábrica concorda com as especificações exigidas. A análise de uma amostra de 200 peças revelou 25 defeituosas. Calcule o tamanho amostral necessário para que o teste tenha um poder de no mínimo 0,9 em detectar a diferença entre a proporção da hipótese nula $p_0$ = 0,9 e uma, possível proporção real de 0,85.
Usamos os dados da tabela abaixo:
| $\mathbf{Poder}$ | $\mathbf{\alpha}$ | $\mathbf{p}$ | $\mathbf{p_0}$ |
| 0,9 | 0,05 | 0,85 | 0,9 |
Fazemos a análise e configuramos conforme a figura de abaixo.
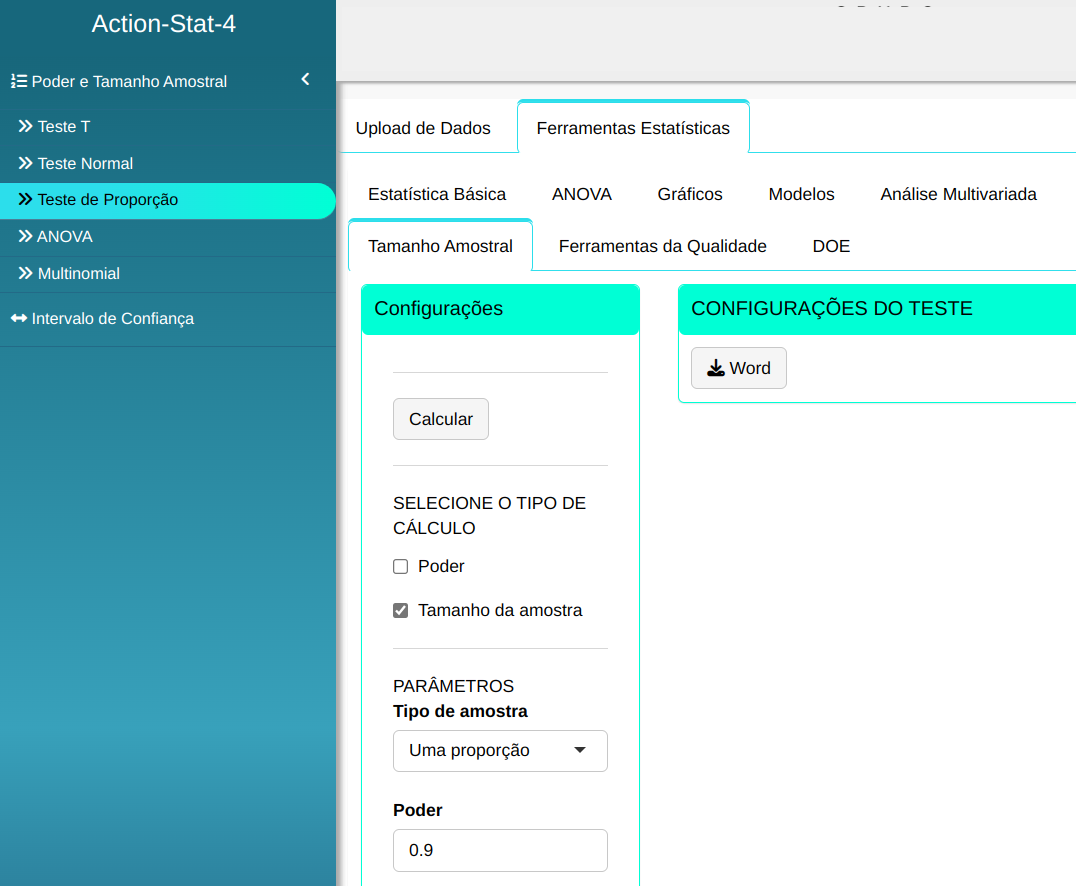
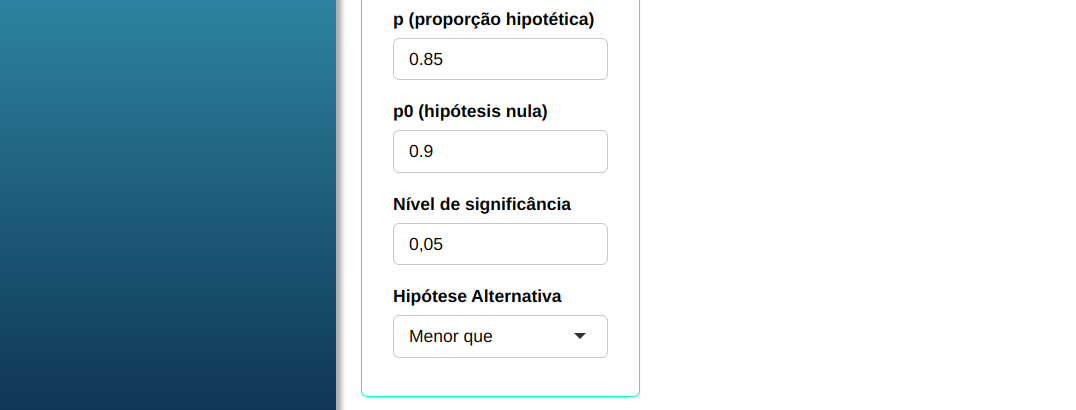
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Resultado da análise
| Aviso | |
| Poder | 0.9 |
| Tamanho da amostra | 372 |
| Proporção hipotética | 0.85 |
| Proporção | 0.9 |
| Nível de significância | 0.05 |
| Hipótese Alternativa | Menor que |
Exemplo 3:
Dadas duas amostras de tamanhos $n_1$ = 100, $n_2$ = 100, calcule o poder do teste de duas proporções em detectar às duas proporções reais $p_1$ = 0,88 e $p_2$ = 0,70 de cada amostra com nível de significância $\alpha$ = 0,05.
Utilizamos os dados da tabela abaixo:
| $\mathbf{n_1}$ | $\mathbf{n_2}$ | $\mathbf{\alpha}$ | $\mathbf{p_1}$ | $\mathbf{p_2}$ |
| 100 | 100 | 0,05 | 0,88 | 0,70 |
Fazemos a análise e configuramos conforme a figura de abaixo.
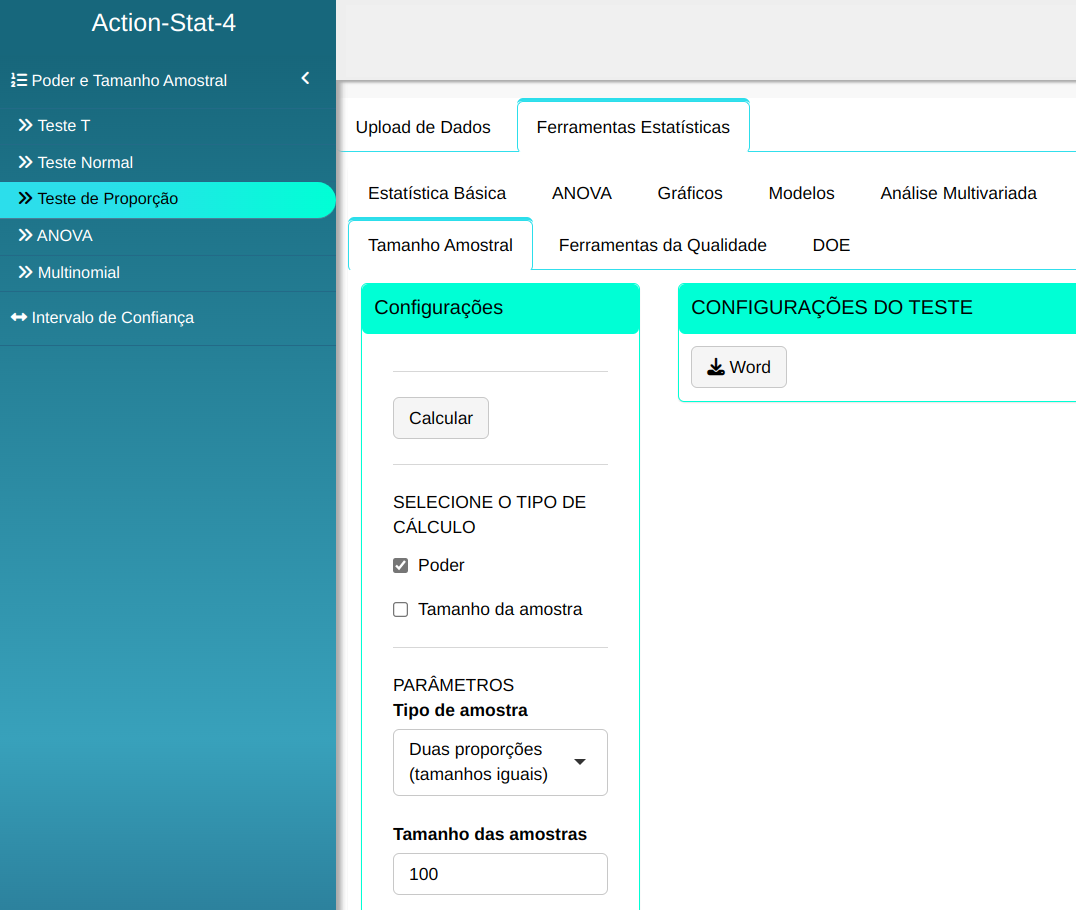
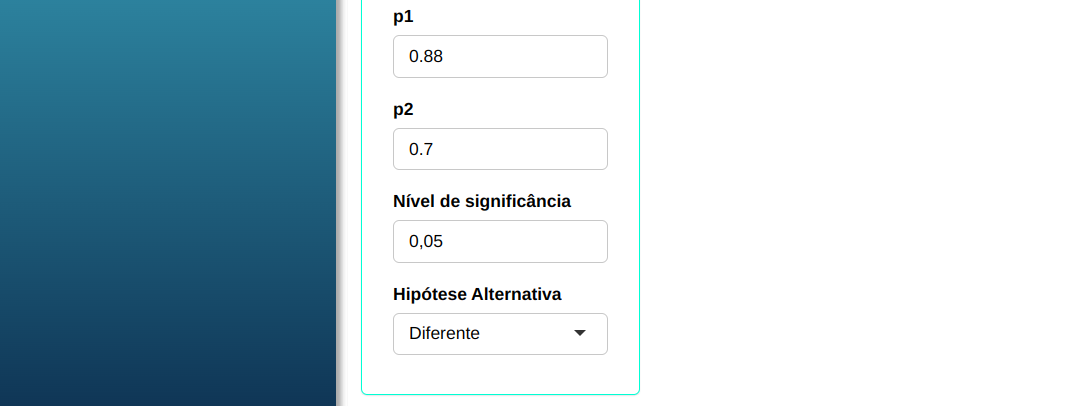
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Resultado da análise
| Aviso | |
| Poder | 0.8915324 |
| Tamanho da amostra | 100 |
| p1 | 0.88 |
| p2 | 0.7 |
| Nível de significância | 0.05 |
| Hipótese Alternativa | Diferente |
Exemplo 4:
Calcule o tamanho de duas amostras para que o teste de duas proporções detecte às duas proporções reais $p_1$ = 0,88 e $p_2$ = 0,80 com poder de, no mínimo 0,9 com nível de significância $\alpha$ = 0,05
Use os dados da tabela abaixo:
| $\mathbf{Poder}$ | $\mathbf{\alpha}$ | $\mathbf{p_1}$ | $\mathbf{p_2}$ |
| 0,9 | 0,05 | 0,88 | 0,80 |
Fazemos a análise e configuramos conforme a figura de abaixo.
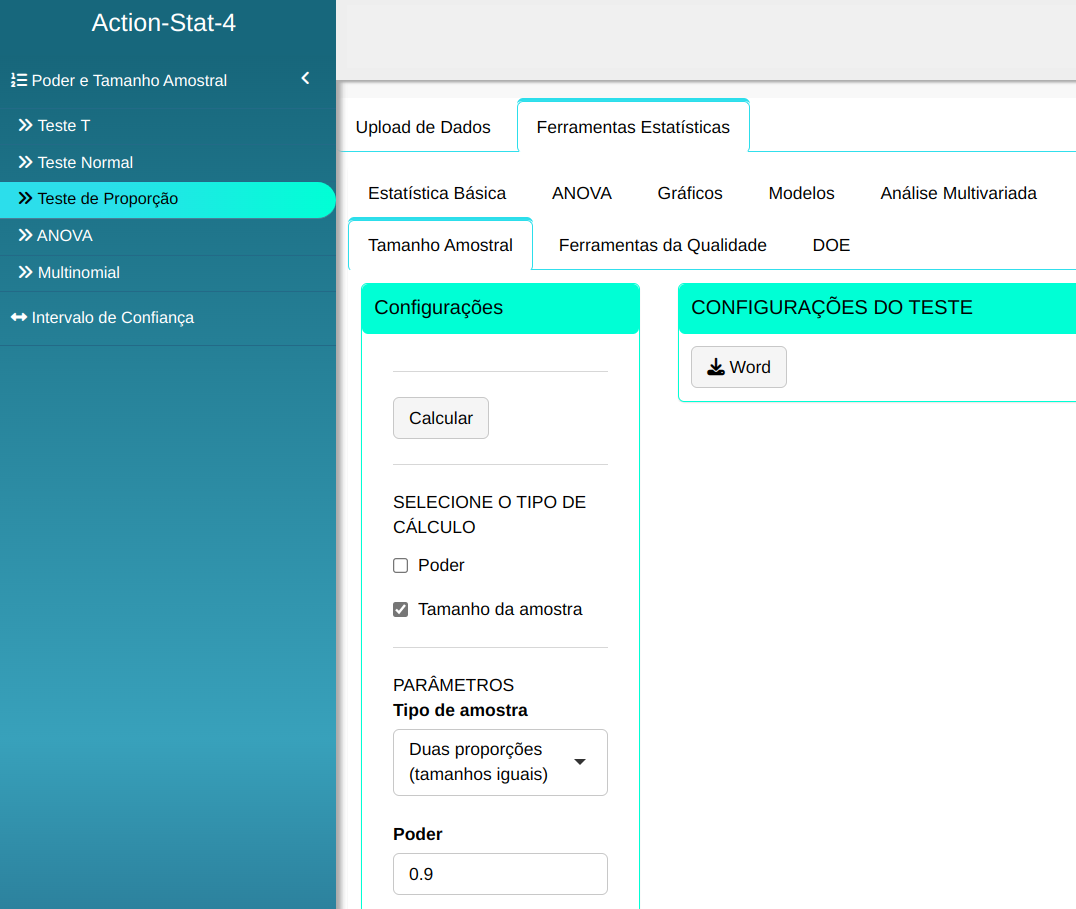
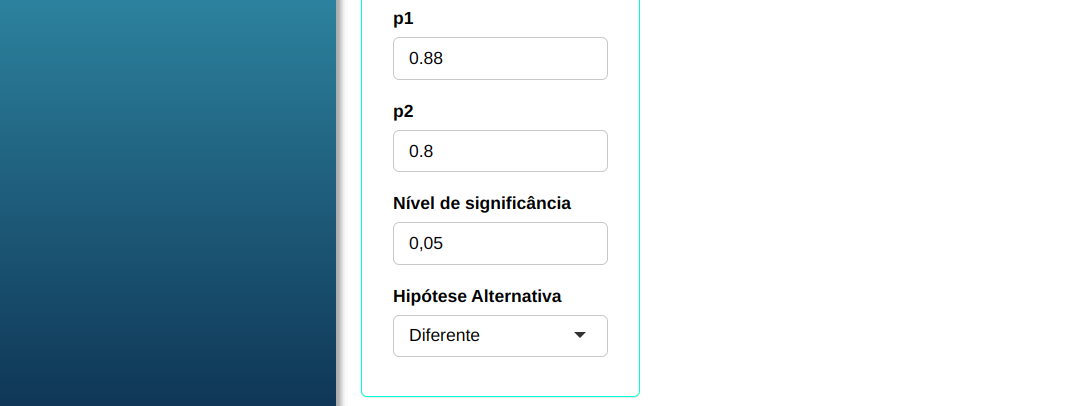
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Resultado da análise
| Aviso | |
| Poder | 0.9 |
| Tamanho da amostra | 435 |
| p1 | 0.88 |
| p2 | 0.8 |
| Nível de significância | 0.05 |
| Hipótese Alternativa | Diferente |
Exemplo 5:
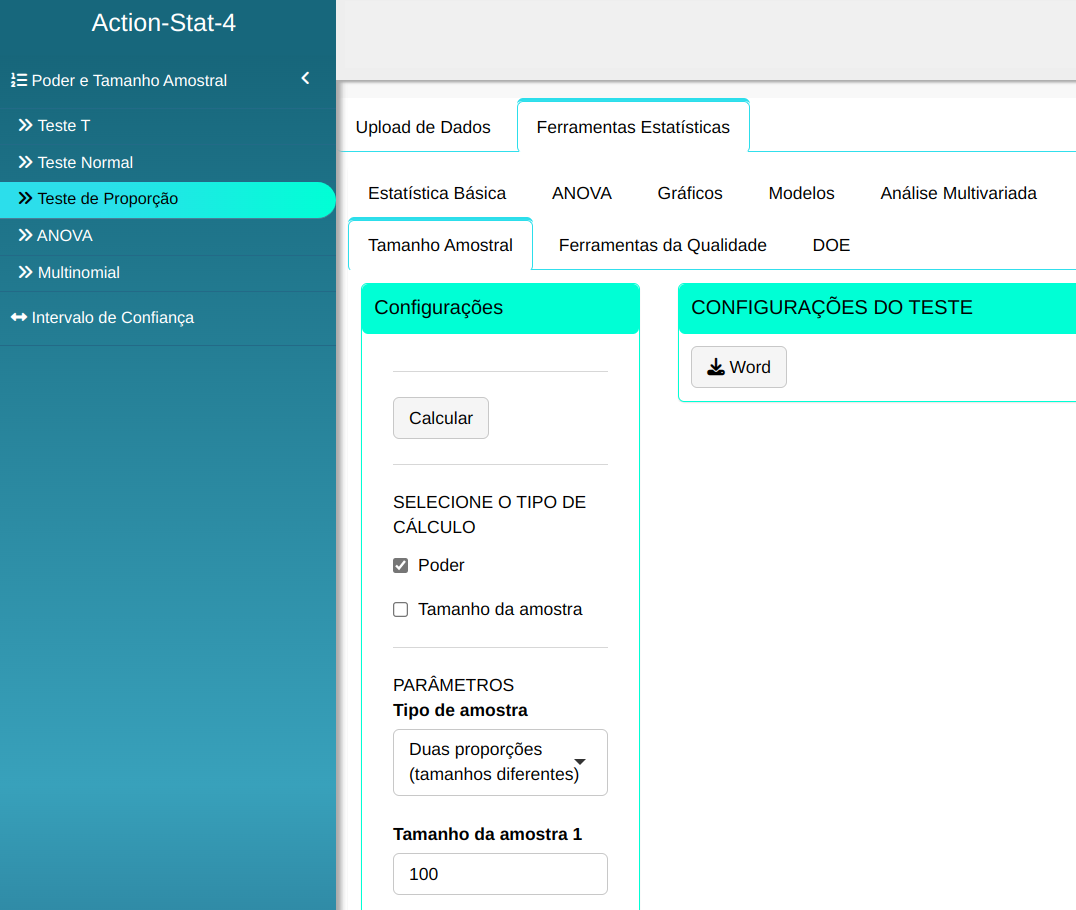
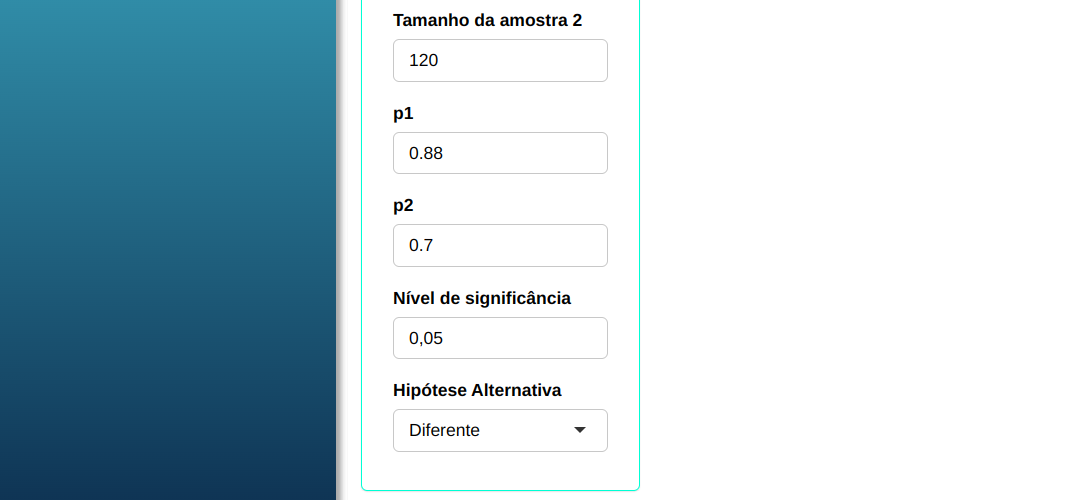
Dadas duas amostras de tamanhos $n_1$ = 100, $n_2$ = 120, calcule o poder do teste de duas proporções em detectar às duas proporções reais $p_1$ = 0,88 e $p_2$ = 0,70 de cada amostra com nível de significância $\alpha$ = 0,05
Utilizamos os dados da tabela abaixo:
| $\mathbf{n_1}$ | $\mathbf{n_2}$ | $\mathbf{\alpha}$ | $\mathbf{p_1}$ | $p_2$ |
| 100 | 120 | 0,05 | 0,88 | 0,70 |
Fazemos a análise e configuramos conforme a figura de abaixo.
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Resultado da análise
| Aviso | |
| Poder | 0.9157088 |
| Tamanho da amostra 1 | 100 |
| Tamanho da amostra 2 | 120 |
| p1 | 0.88 |
| p2 | 0.7 |
| Nível de significância | 0.05 |
| Hipótese Alternativa | Diferente |
Exemplo 6:
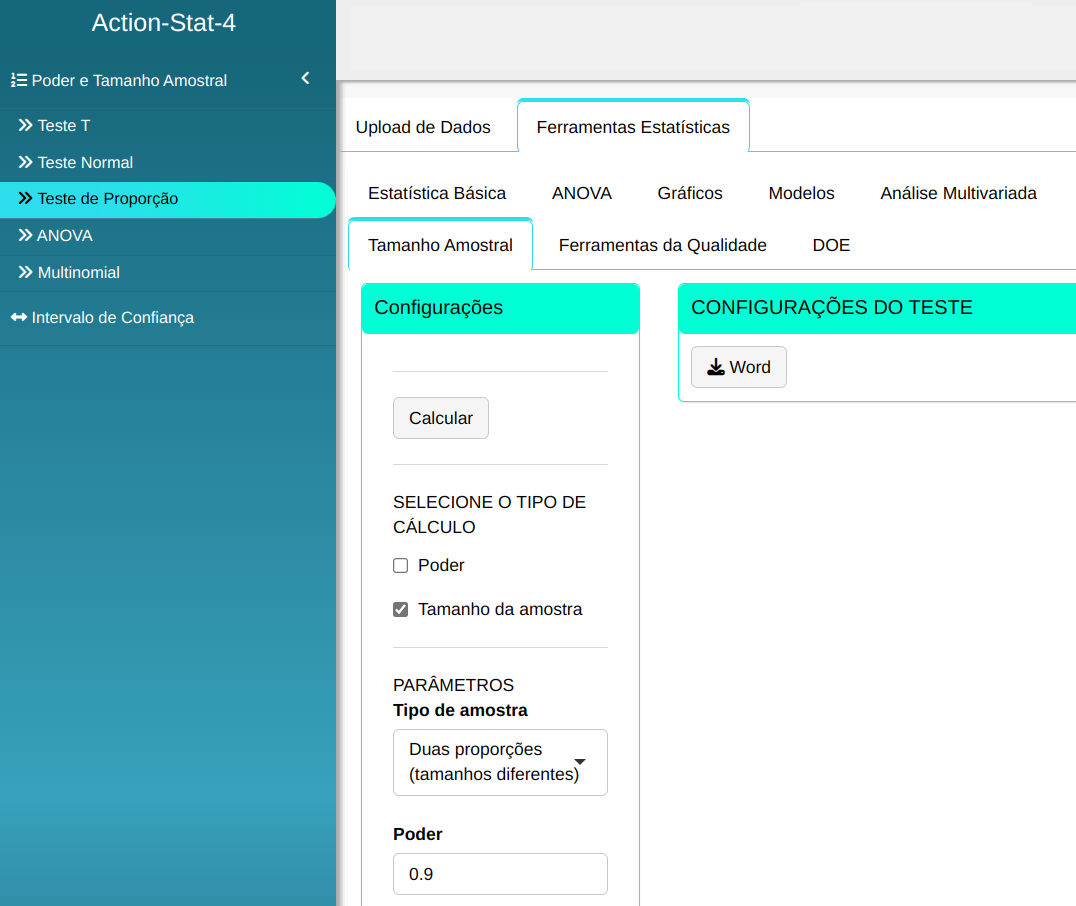
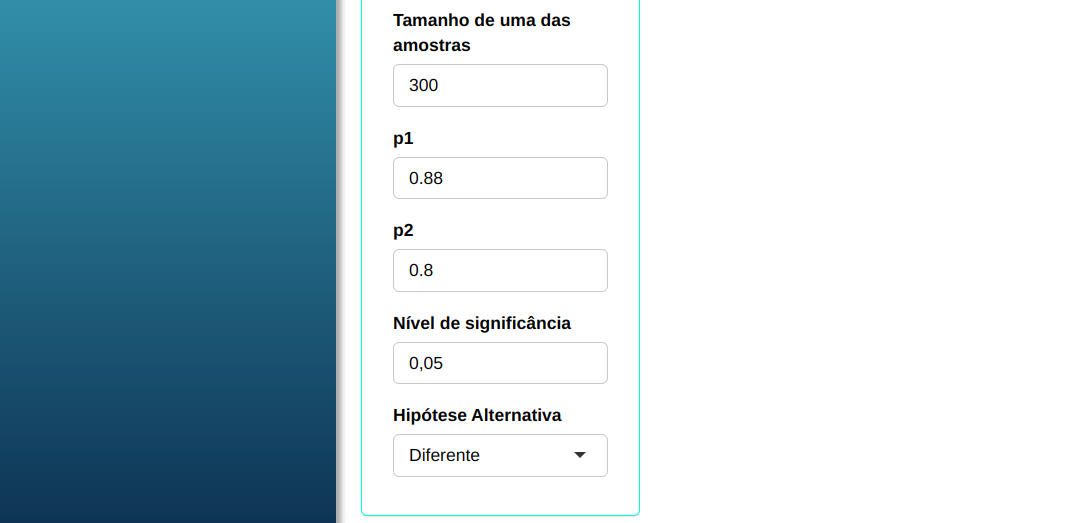
Dado o tamanho de uma amostra igual a $n_1$ = 300, calcule o tamanho da outra amostra para que o teste de duas proporções detecte as duas proporções reais $p_1$ = 0,88 e $p_2$ = 0,80 com poder de, no mínimo 0,9, com nível de significância $\alpha$ = 0,05.
Use os dados da tabela abaixo:
| $\mathbf{Poder}$ | $\mathbf{\alpha}$ | $\mathbf{p_1}$ | $\mathbf{p_2}$ | $\mathbf{n_1}$ |
| 0,9 | 0,05 | 0,88 | 0,80 | 300 |
Fazemos a análise e configuramos conforme a figura de abaixo.
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Resultado da análise
| Aviso | |
| Poder | 0.9 |
| Tamanho da amostra 1 | 300 |
| Tamanho da amostra 2 | 791 |
| p1 | 0.88 |
| p2 | 0.8 |
| Nível de significância | 0.05 |
| Hipótese Alternativa | Diferente |