2. Teste Normal
Aqui o Teste Normal é utilizado para calcular o poder do teste ou o tamanho da amostra.
Exemplo 1:
Um supervisor da qualidade quer testar, com base numa amostra aleatória de tamanho n = 35 e para um nível de significância $\alpha$ = 0,05, se a profundidade média de um furo numa determinada peça é 72,4mm. Qual o poder do teste em detectar uma diferença de 1,2 entre a média real da população e a média estabelecida pela hipótese nula se sabemos, de informações anteriores, que $\sigma$ = 2,1 mm?
Primeiro vamos estabelecer as hipóteses:
$\qquad \quad \begin{cases} H_0: \mu = 72,4 \text{ mm} \cr H_1: \mu \neq 72,4 \text{ mm} \end{cases}$
Para o cálculo do poder deste teste de hipóteses, utilizaremos os seguintes dados
| $\mathbf{\sigma}$ | $\mathbf{n}$ | $\mathbf{\alpha}$ | diferença |
| 2,1 | 35 | 0,05 | 1,2 |
Fazemos a análise e configuramos conforme a figura de abaixo.
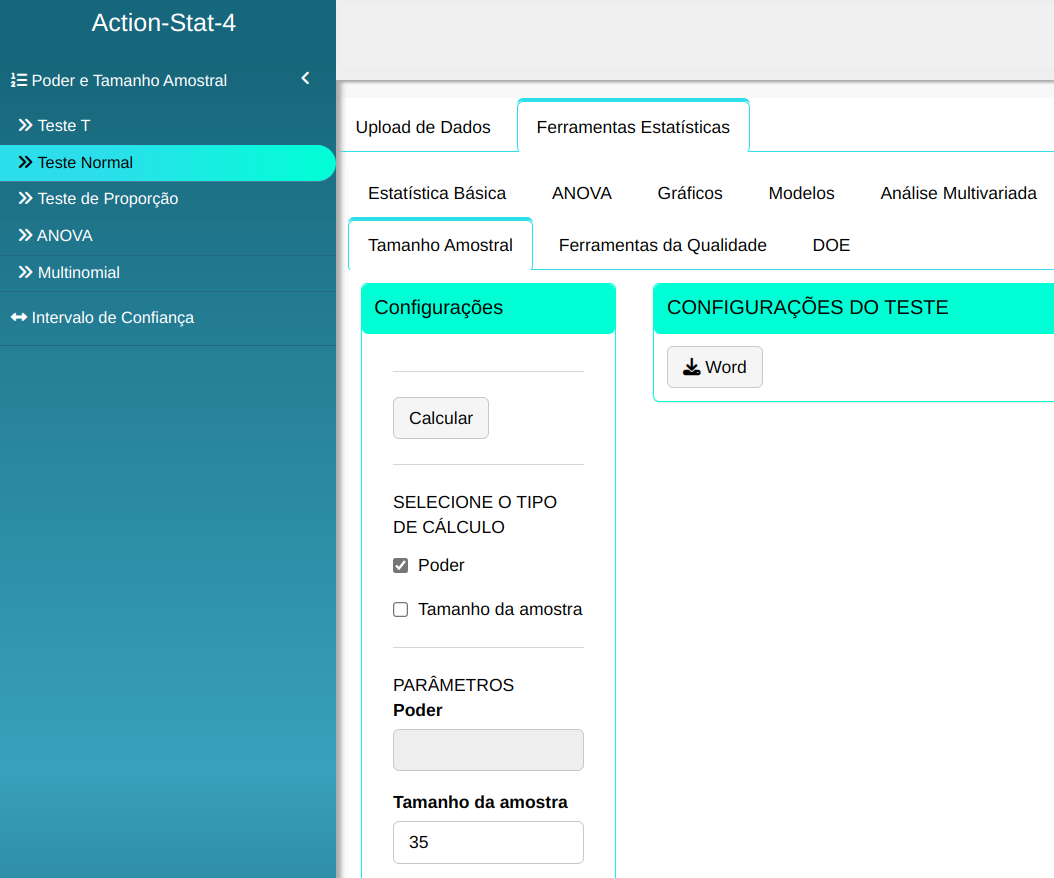
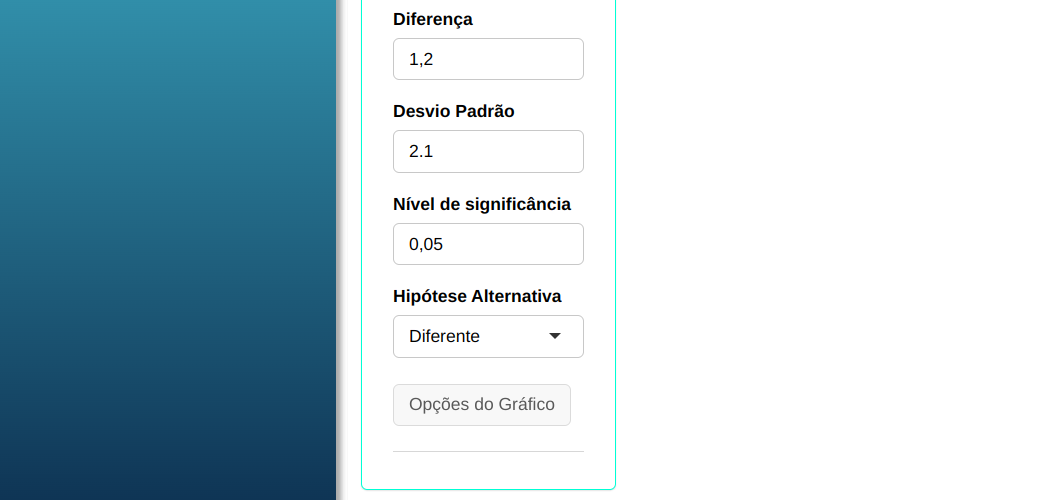
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Teste normal
| V1 | |
|---|---|
| Poder | 0.9222912 |
| Tamanho da amostra | 35 |
| Diferença | 1.2 |
| Desvio padrão | 2.1 |
| Nível de significância | 0.05 |
| Hipótese Alternativa | Diferente |
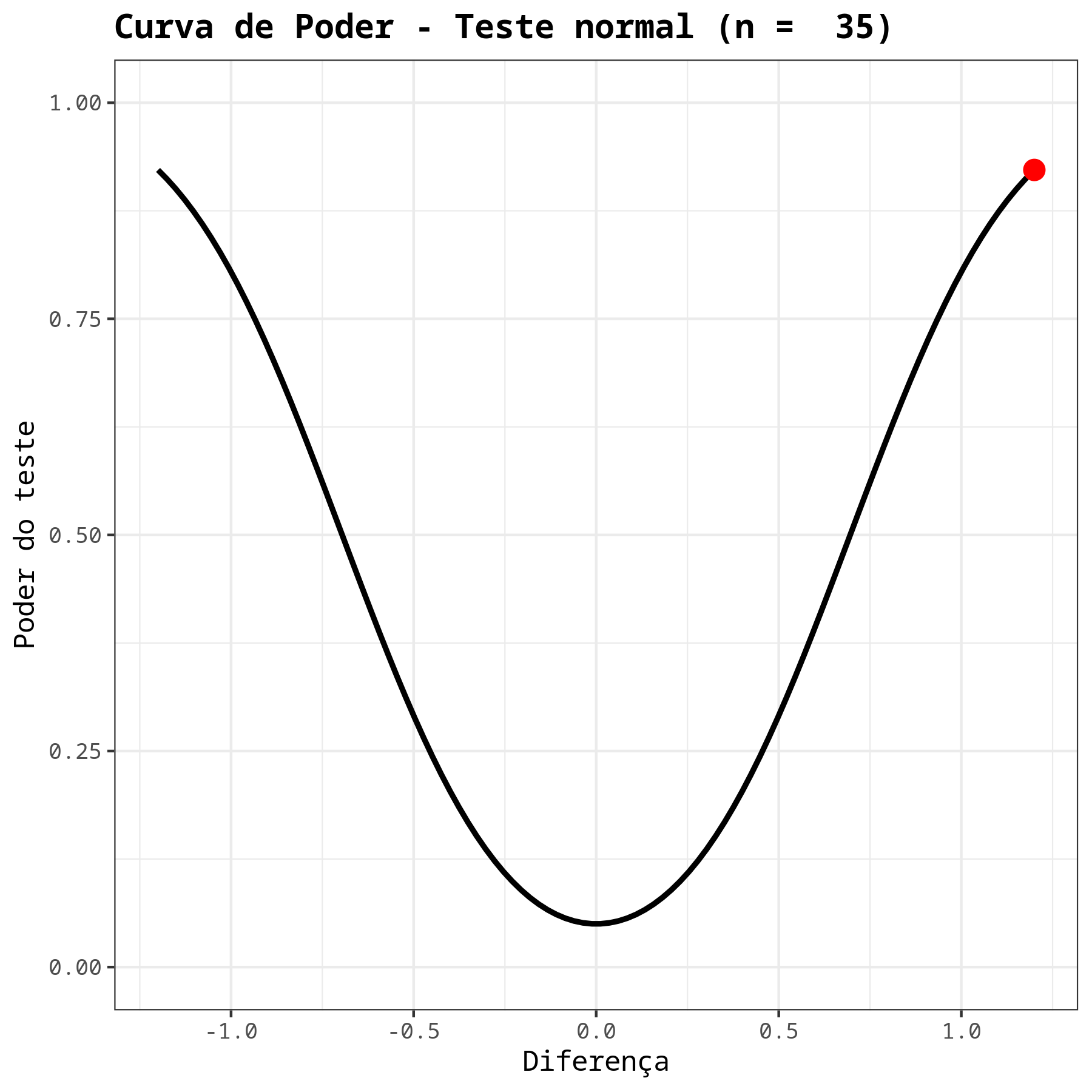
Com isso, concluímos que o poder do teste de hipóteses em detectar uma diferença d = 1,2 entre o valor real da média populacional e o valor estabelecido pela hipótese nula é de, aproximadamente, 92,23%.
Exemplo 2:
Qual o tamanho amostral necessário para que, a um nível de significância $\alpha$ = 0,05, um teste de hipóteses normal detecte uma diferença d = 0,6 entre a média populacional e a média estabelecida pela hipótese nula com poder de, no mínimo 0,9 sabendo de informações anteriores, que $\sigma$ = 2,1 mm?
Primeiro vamos estabelecer as hipóteses:
$\qquad \quad \begin{cases} H_0: \mu = 72,4 \text{ mm} \cr H_1: \mu \neq 72,4 \text{ mm} \end{cases}$
Usaremos os dados da tabela abaixo:
| $\mathbf{\sigma}$ | Poder | $\mathbf{\alpha}$ | diferença |
| 2,1 | 0,9 | 0,05 | 0,6 |
Fazemos a análise e configuramos conforme a figura de abaixo.
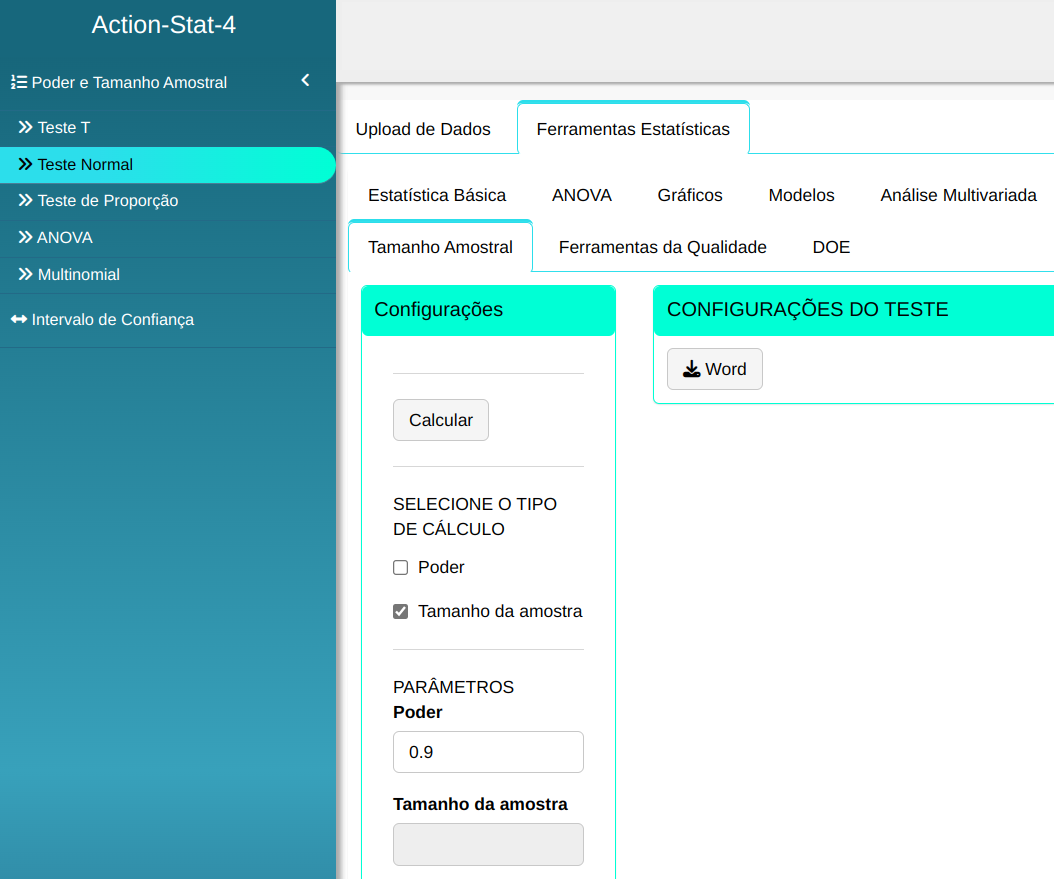
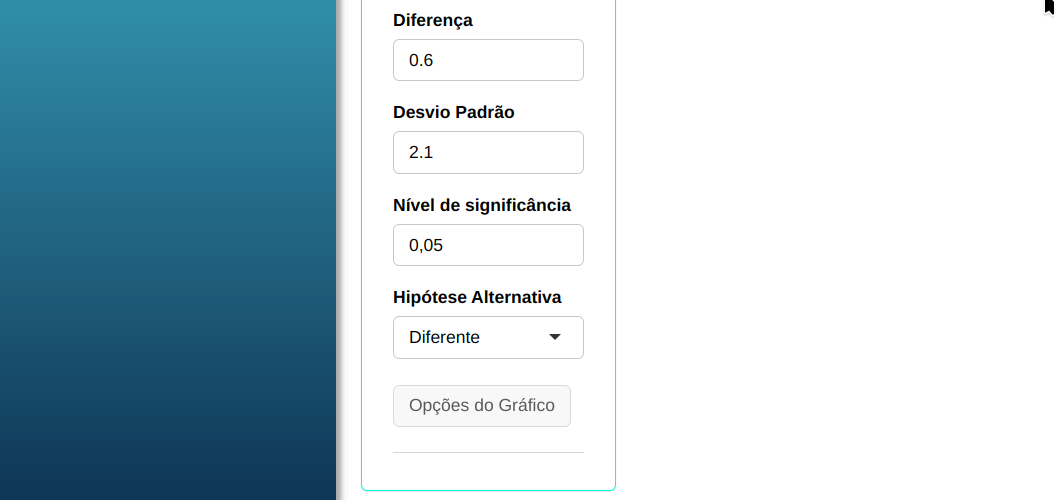
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Teste normal
| V1 | |
|---|---|
| Poder | 0.9 |
| Tamanho da amostra | 129 |
| Diferença | 0.6 |
| Desvio padrão | 2.1 |
| Nível de significância | 0.05 |
| Hipótese Alternativa | Diferente |
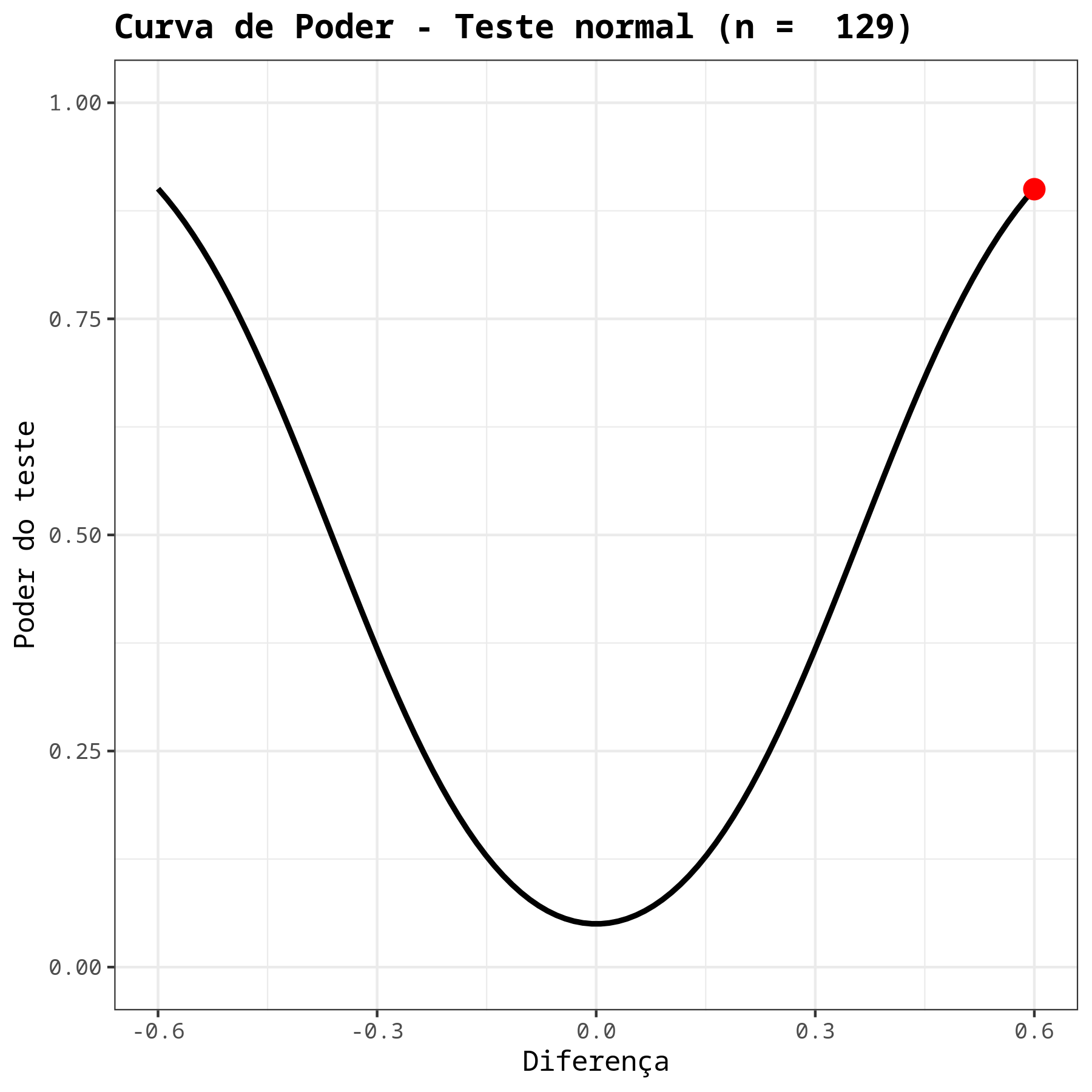
Portanto, para que o teste detecte uma diferença de 0,6 com um poder de, no mínimo 0,9, é necessário um tamanho amostral de 129 elementos.
Exemplo 3:
O gerente de produção de uma empresa tem como objetivo avaliar a performance de uma nova metodologia de ensino para novos operários contratados. Com a metodologia antiga, tem-se uma taxa média de 4 erros por operário na primeira semana de trabalho. Em uma amostra de 25 operários foi aplicada a nova metodologia e observou-se que a média foi de 5 erros por semana com desvio padrão de 2. Com essas informações calcule o poder do teste em se detectar uma diferença d = 0,25 entre a taxa verdadeira e a taxa da hipótese nula com um nível de significância $\alpha$ = 0,05.
Utilizaremos os dados da tabela abaixo:
| $\mathbf{\sigma}$ | $\mathbf{n}$ | $\mathbf{\alpha}$ | diferença |
| 2 | 25 | 0,05 | 1 |
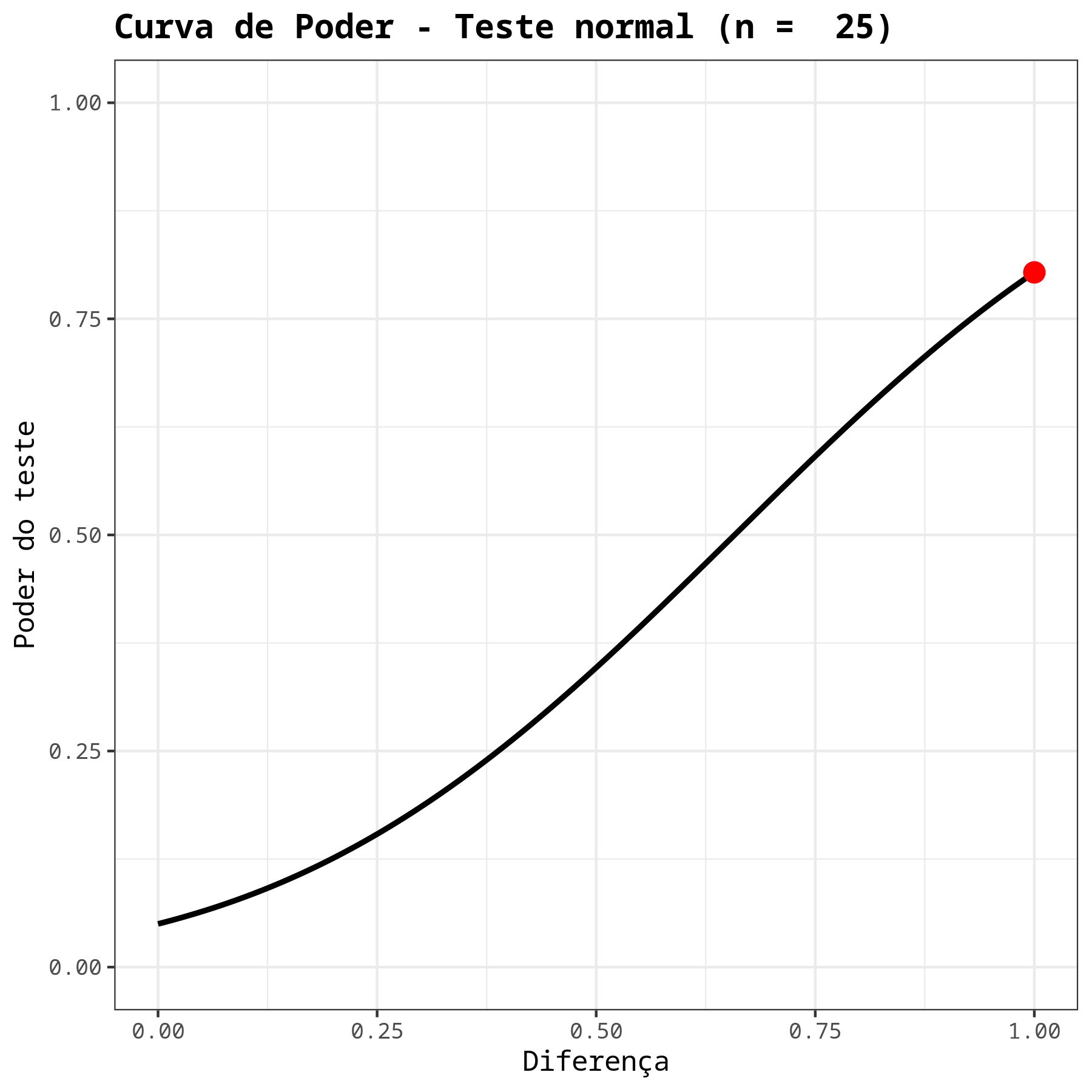
Fazemos a análise e configuramos conforme a figura de abaixo.
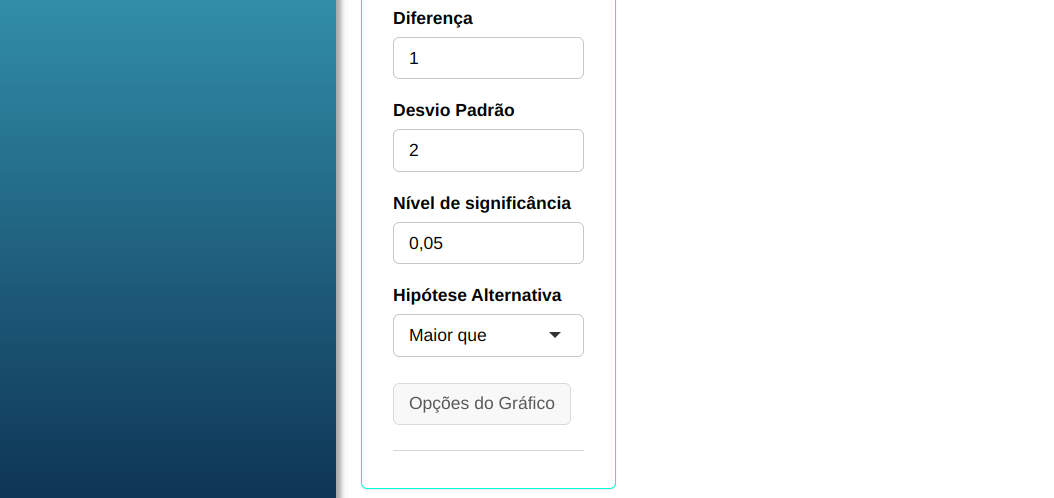
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Teste normal
| V1 | |
|---|---|
| Poder | 0.8037649 |
| Tamanho da amostra | 25 |
| Diferença | 1 |
| Desvio padrão | 2 |
| Nível de significância | 0.05 |
| Hipótese Alternativa | Maior que |
Exemplo 4:
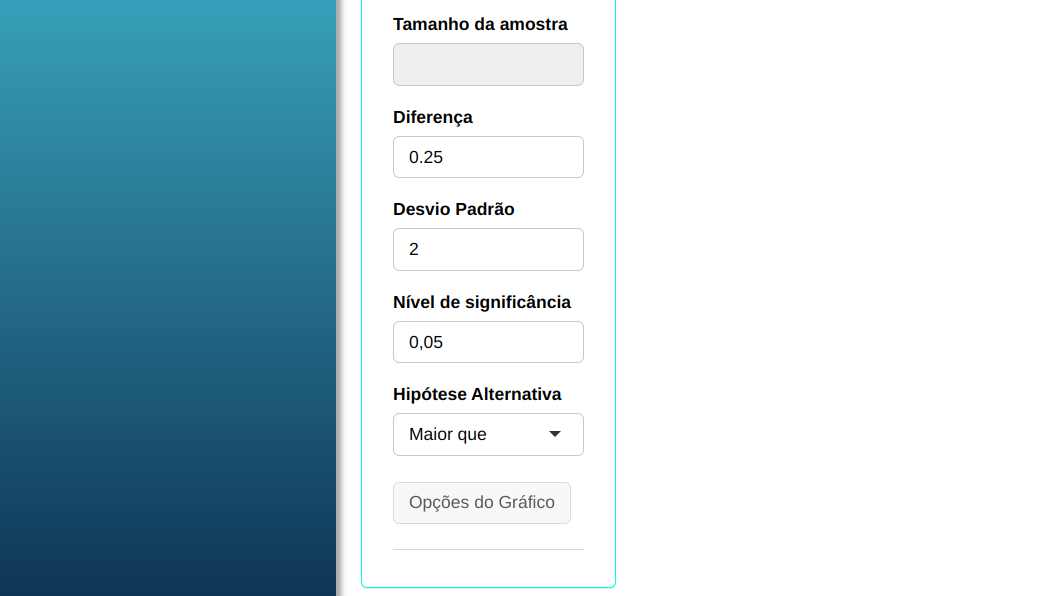
O gerente de produção de uma empresa tem como objetivo avaliar a performance de uma nova metodologia de ensino para novos operários contratados. Com a metodologia antiga, tem-se uma taxa média de 4 erros por operário na primeira semana de trabalho. Em uma amostra de 25 operários foi aplicada a nova metodologia e observou-se que a média foi de 5 erros por semana. Sabendo que o desvio padrão é igual a 2, calcule o tamanho amostral necessário para que o teste detecte uma diferença d = 0,25 entre a taxa real e a taxa assumida pela hipótese nula com poder de, no mínimo, 0,9 a um nível de significância $\alpha$ = 0,05.
Use os dados da tabela abaixo:
| $\mathbf{\sigma}$ | Poder | $\mathbf{\alpha}$ | diferença |
| 2 | 0,9 | 0,05 | 0,25 |
Fazemos a análise e configuramos conforme a figura de abaixo.
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Teste normal
| V1 | |
|---|---|
| Poder | 0.9 |
| Tamanho da amostra | 549 |
| Diferença | 0.25 |
| Desvio padrão | 2 |
| Nível de significância | 0.05 |
| Hipótese Alternativa | Maior que |
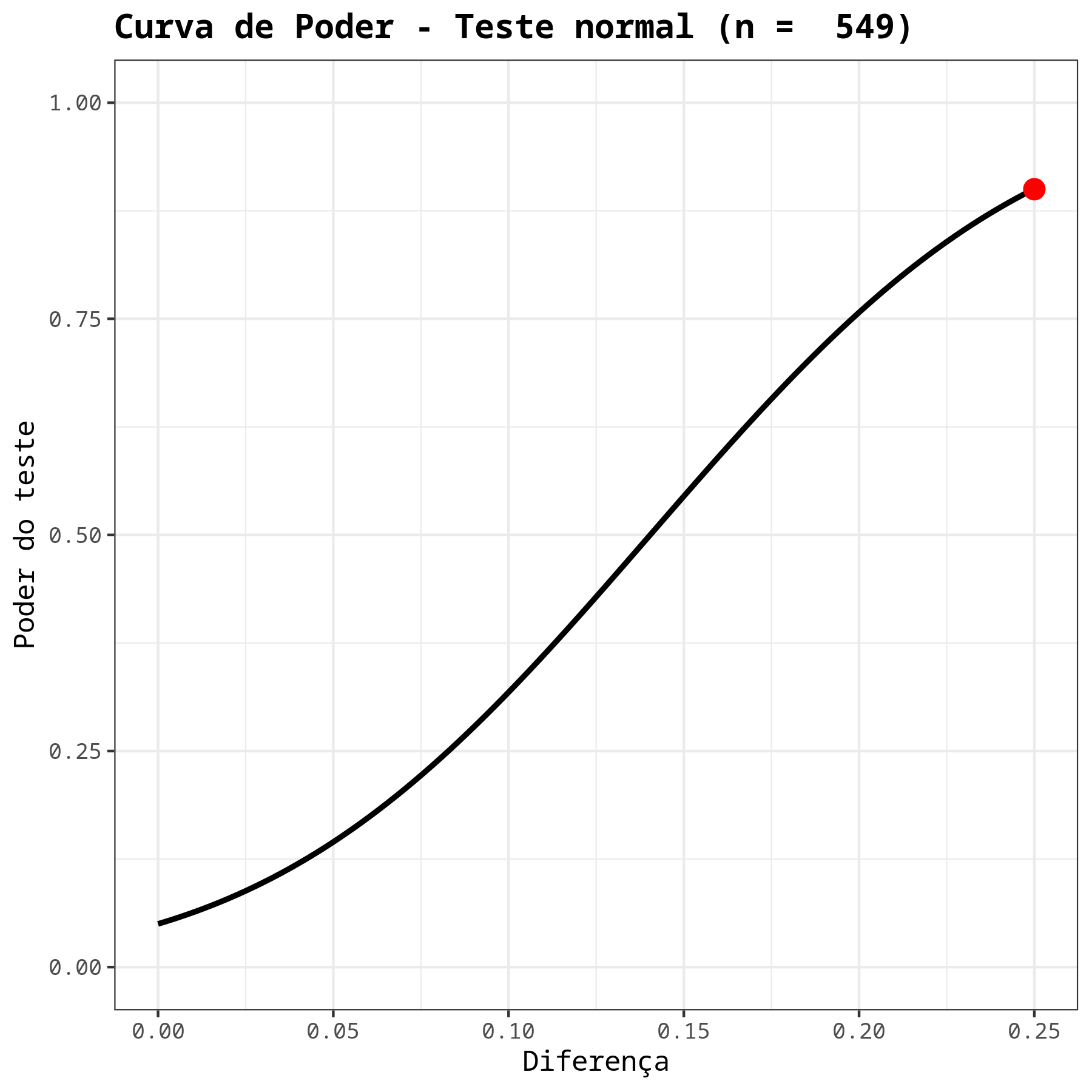
Ou seja, para que o teste detecte uma diferença d = 0,25 com um poder de, no mínimo 0,9, é necessário que tomemos uma amostra de 549 elementos.