1. Teste T
Aqui o Teste T é utilizado para calcular o poder do teste de hipóteses ou o tamanho da amostra.
Exemplo 1:
Um Engenheiro de produção pretende testar, com base nos dados da tabela a seguir e para um nível de significância $\alpha$ = 0,05, se a altura média de uma haste está próxima do valor nominal de 1055 mm. Para isso, foi analisada uma amostra de 20 hastes, cujas medidas encontram-se na tabela.
| 903,88 |
| 1020,7 |
| 934,52 |
| 860,41 |
| 936,78 |
| 1036,92 |
| 915,38 |
| 1214,08 |
| 1039,19 |
| 1086,98 |
| 1098,04 |
| 1014,53 |
| 993,45 |
| 950,38 |
| 1144,94 |
| 1011,26 |
| 1097,79 |
| 1120,19 |
| 941,83 |
| 1066,12 |
Neste caso, estabelecemos as hipóteses
- $H_0$: $\mu =$ 1055
- $H_1$: $\mu \neq $ 1055
Utilizando a ferramenta Resumo descritivo do menu de Estatística Básica do Action, temos que a média amostral é $\overline{X}=$ 1019,3685 e o desvio padrão amostral é s $=$ 91,36863255.
Então calcularemos o poder do teste T considerando os seguintes valores
| $\quad\mathbf{\sigma}$ | $\mathbf{n}$ | nível de significância |
| 91,37 | 20 | $\qquad \quad$ 0,05 |
Para calcular o Poder de um teste de hipóteses, calculamos a probabilidade de se rejeitar a hipótese nula quando esta é realmente falsa, ou seja, a hipótese alternativa é verdadeira. Assim, assumimos um valor x para a hipótese alternativa e o poder do teste é a probabilidade que o teste possui de detectar a diferença d entre o valor x da hipótese alternativa e o valor da hipótese nula.
Faremos o Upload dos dados no sistema.
Para realizar o teste, configuramos conforme a figura abaixo.
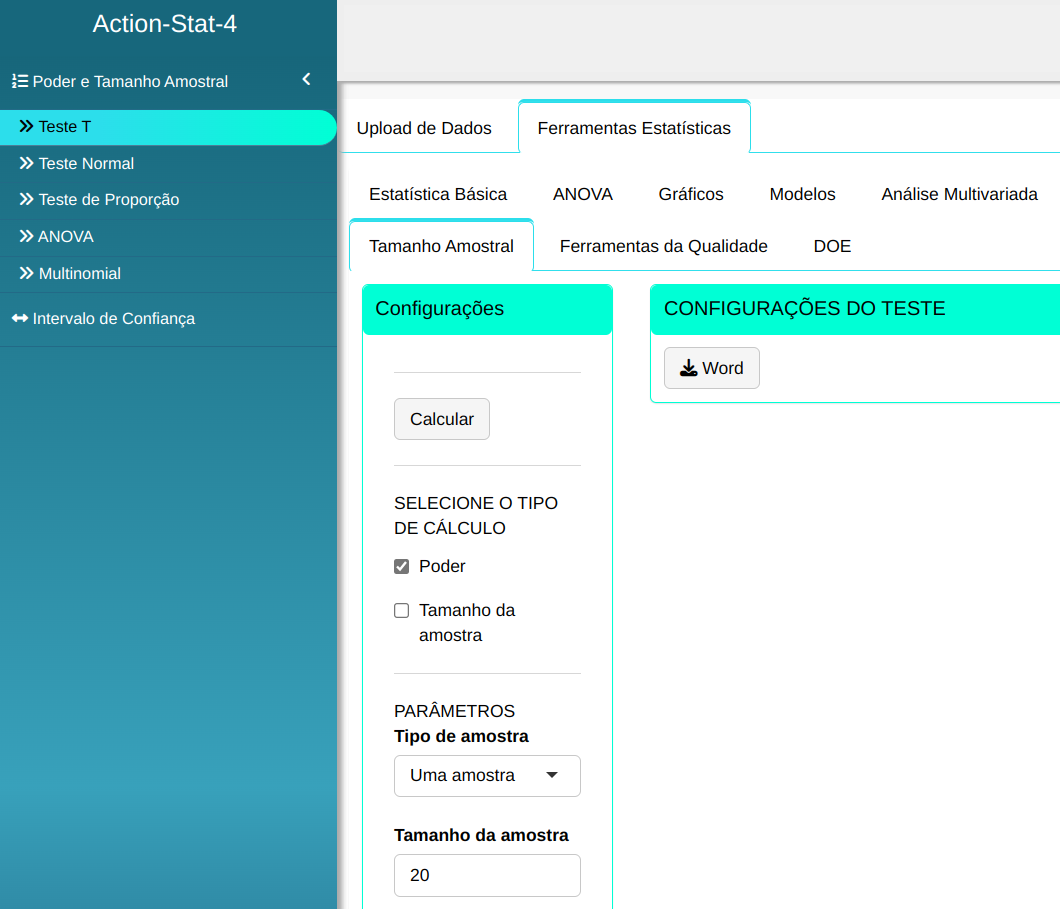
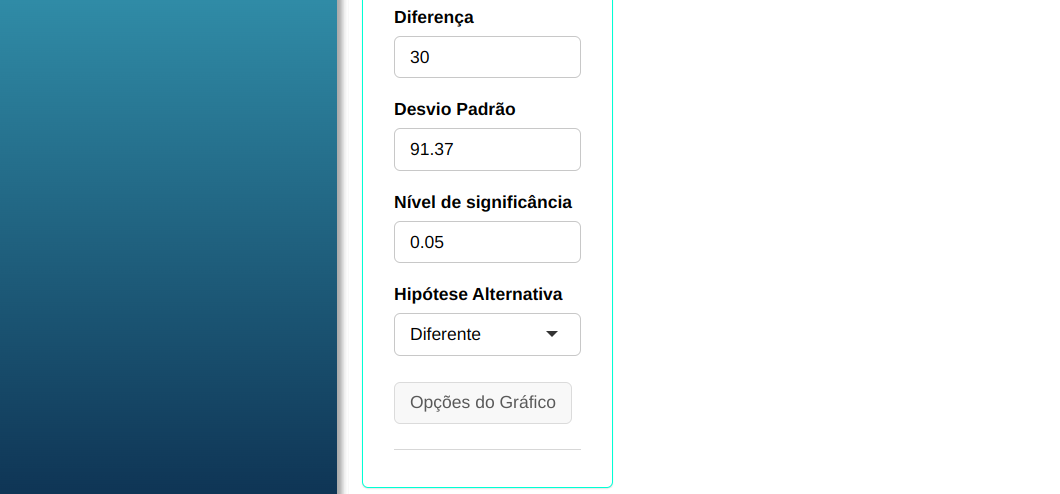
Clique em Calcular para obter os resultados. Também pode baixar os resultados no formato Word.

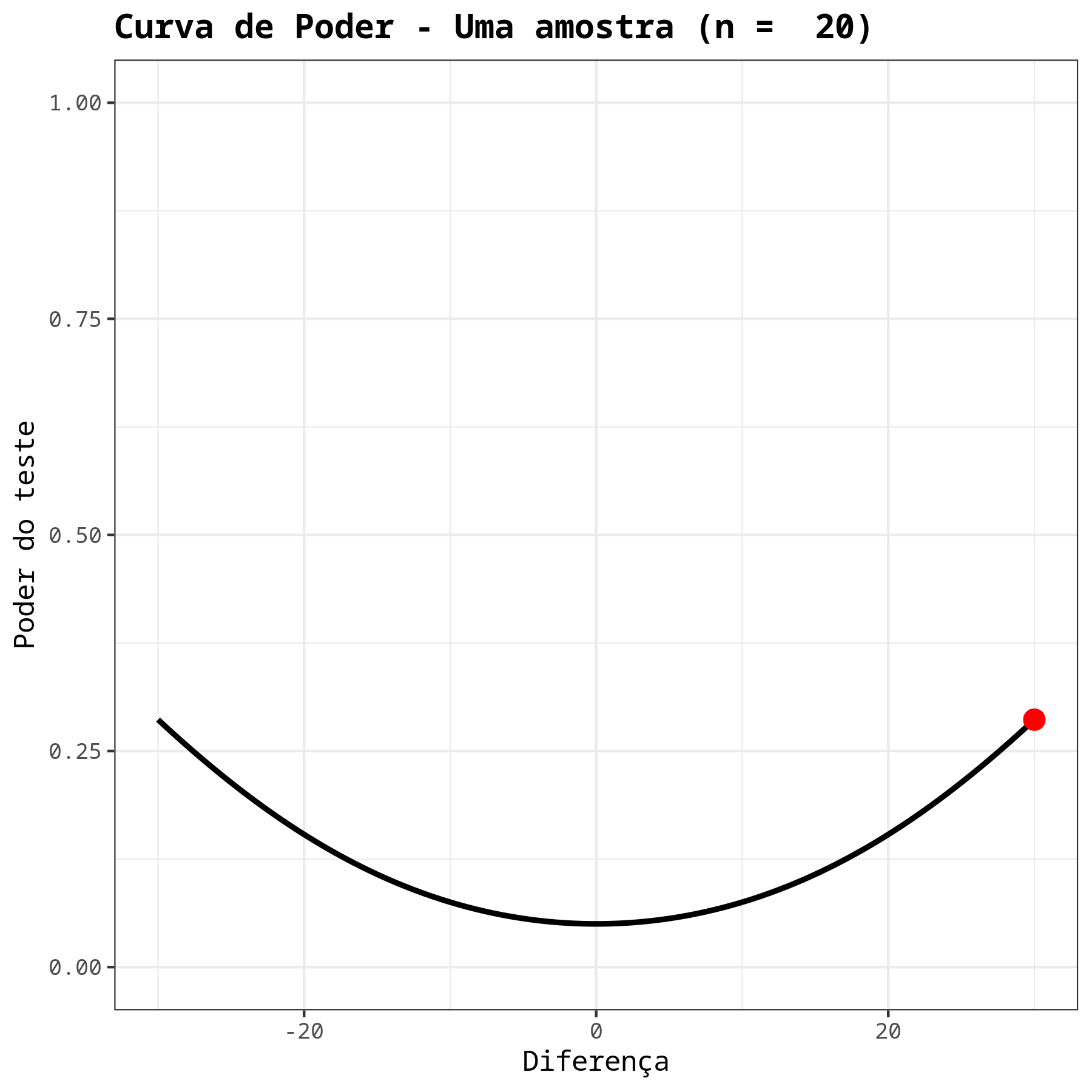
Os resultados são:
Teste T - Uma amostra
| V1 | |
|---|---|
| Poder | 0.2863009 |
| Tamanho da amostra | 20 |
| Diferença | 30 |
| Nível de significância | 0.05 |
| Desvio padrão | 91.37 |
| Hipótese Alternativa | Diferente |
Exemplo 2:
Usando os mesmos dados no exemplo anterior, suponha agora, que se deseje calcular o tamanho amostral necessário para que o teste T detecte uma diferença de 30mm com, no mínimo, um poder de 90%
| 903,88 |
| 1020,7 |
| 934,52 |
| 860,41 |
| 936,78 |
| 1036,92 |
| 915,38 |
| 1214,08 |
| 1039,19 |
| 1086,98 |
| 1098,04 |
| 1014,53 |
| 993,45 |
| 950,38 |
| 1144,94 |
| 1011,26 |
| 1097,79 |
| 1120,19 |
| 941,83 |
| 1066,12 |
Faremos o Upload dos dados no sistema.

Para realizar o teste, configuramos conforme a figura de abaixo.
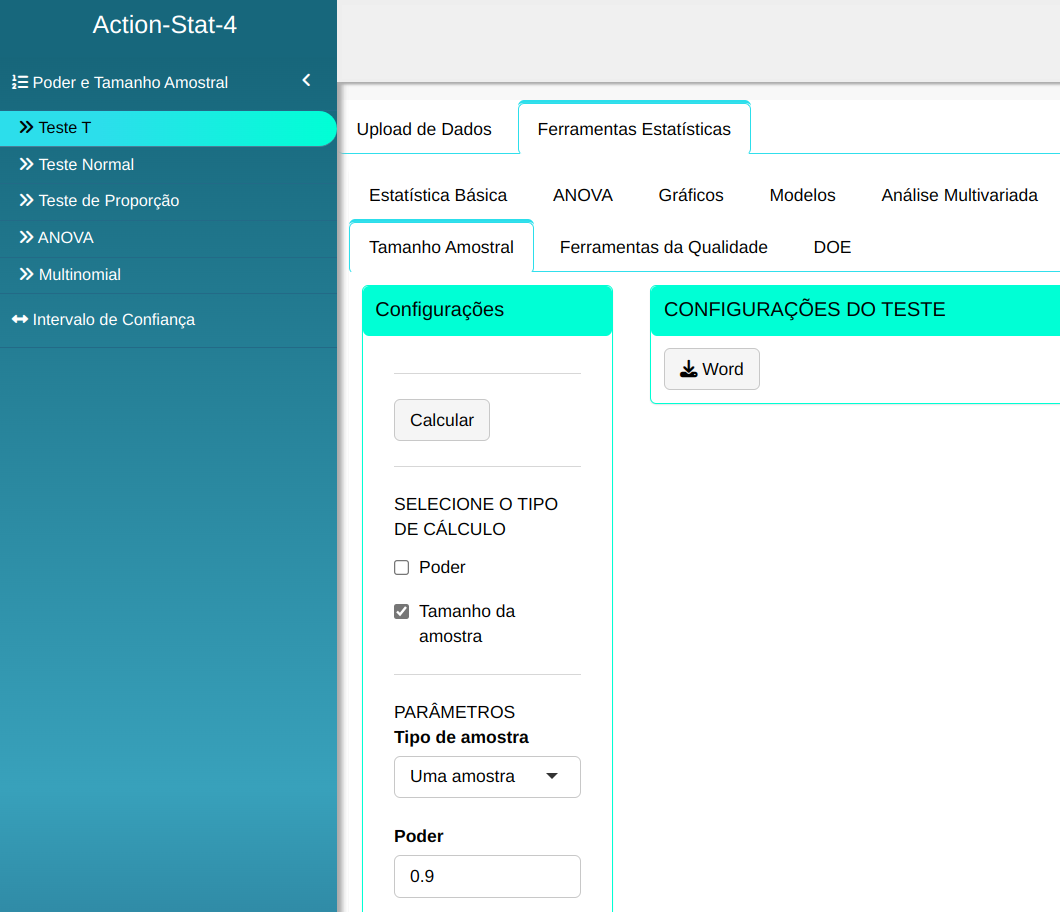
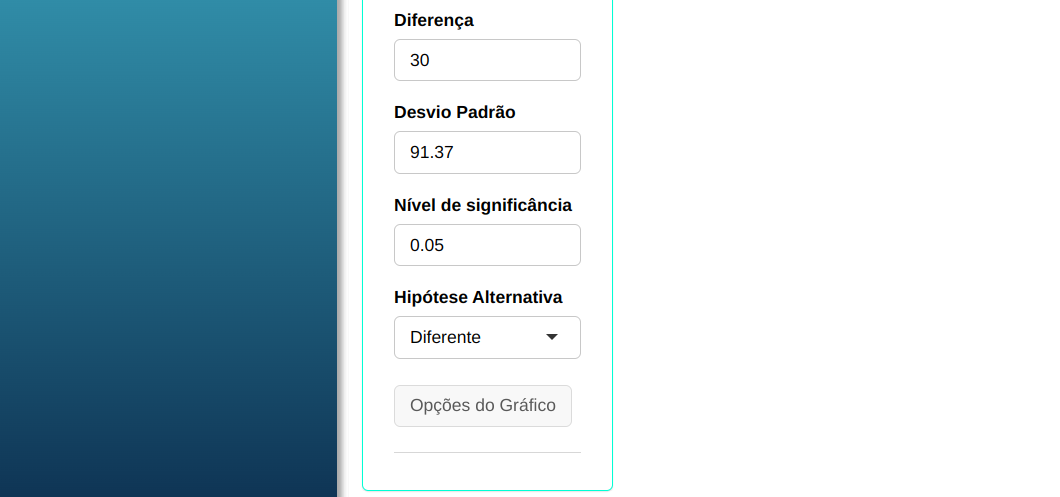
Clique em Calcular para obter os resultados. Também pode baixar os resultados no formato Word.
Os resultados são:
Teste T - Uma amostra
| V1 | |
|---|---|
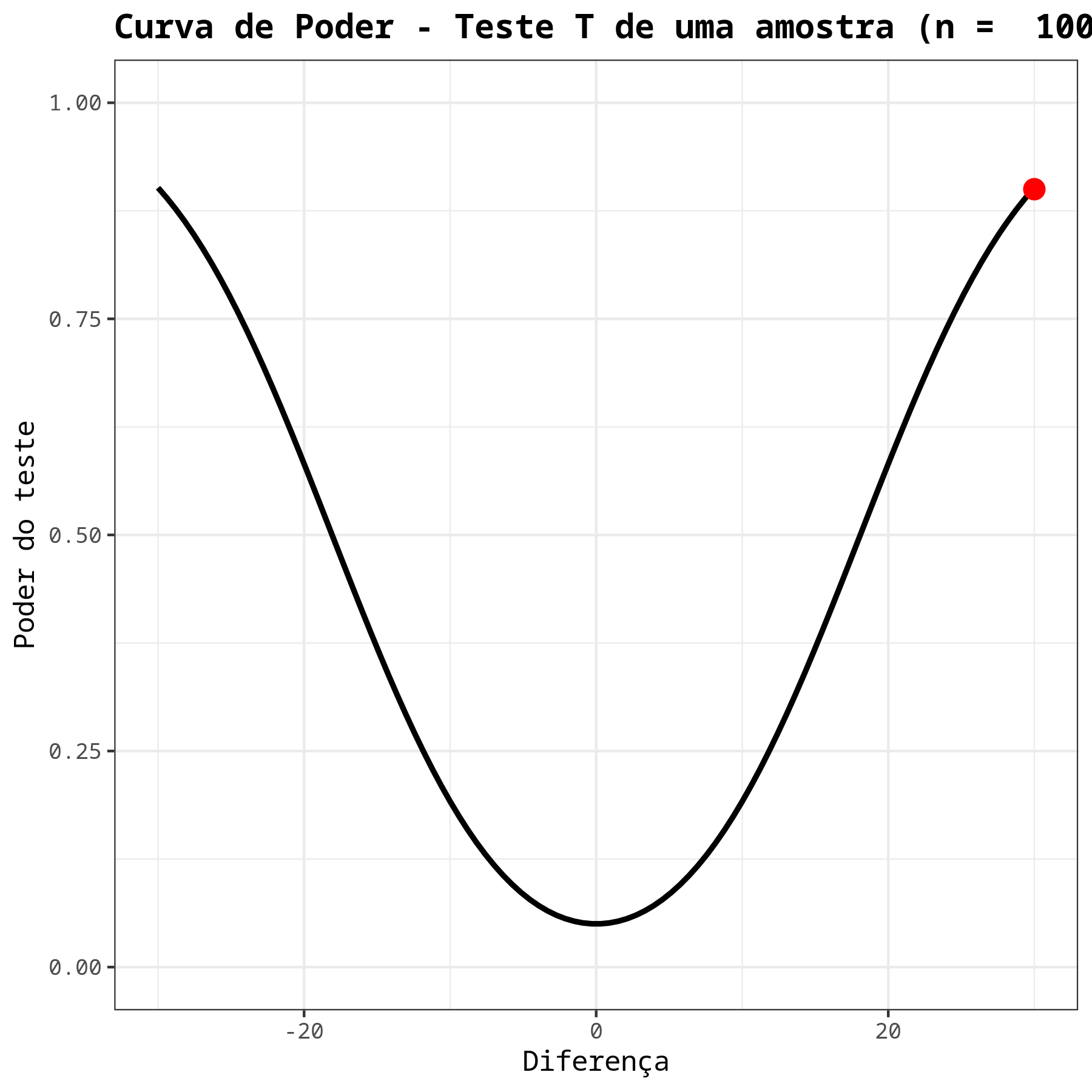
| Poder | 0.9 |
| Tamanho da amostra | 100 |
| Diferença | 30 |
| Nível de significância | 0.05 |
| Desvio padrão | 91.37 |
| Hipótese Alternativa | Diferente |
Exemplo 3:
Considerando os dados abaixo, compare as médias das amostras.
| Amostra 1 | Amostra 2 |
|---|---|
| 976,46 | 982,82 |
| 1106,84 | 949,61 |
| 1073,73 | 1128,40 |
| 1022,91 | 1127,82 |
| 1102,38 | 960,57 |
| 930,62 | 967,27 |
| 1104,27 | 1095,48 |
| 1007,22 | 996,85 |
| 1114,63 | 1087,26 |
| 1093,14 | 1086,14 |
| 923,04 | 937,53 |
| 1044,95 | 1088,24 |
| 929,86 | 1018,75 |
| 1102,16 | 1131,13 |
| 919,15 | 949,66 |
| 962,61 | 1121,67 |
| 1039,07 | 953,73 |
| 1111,61 | 970,52 |
| 1044,90 | 952,71 |
| 1032,52 | 1066,47 |
| 1100,22 | 939,22 |
| 1100,82 | 1052,59 |
| 931,91 | 947,21 |
| 951,91 | 1086,75 |
| 1024,30 | 1124,85 |
Estabelecer as hipóteses:
- $H_0$: $\mu_1 - \mu_2 = $ 0
- $H_1$: $\mu_1 - \mu_2 \neq $ 0
Para calcular o poder do teste T de duas amostras de mesmo tamanho, a fim de detectar uma diferença $\mu_1 - \mu_2 = $30, é necessário determinar o desvio padrão. Por meio da ferramenta Resumo descritivo do Action, obtiveram-se os valores $s_1 = $70,54 e $s_2 = $73,63.
| $\mathbf{n_1 = n_2}$ | $\mathbf{\alpha}$ | Diferença $\mathbf{(\mu_1 - \mu_2)}$ | Desvio-Padrão 1 | Desvio-Padrão 2 |
| $\quad$ 25 | 0,05 | $\qquad$ 30 | $\quad \quad$ 70,54 | $\qquad$ 73,63 |
Faremos o upload dos dados no sistema.
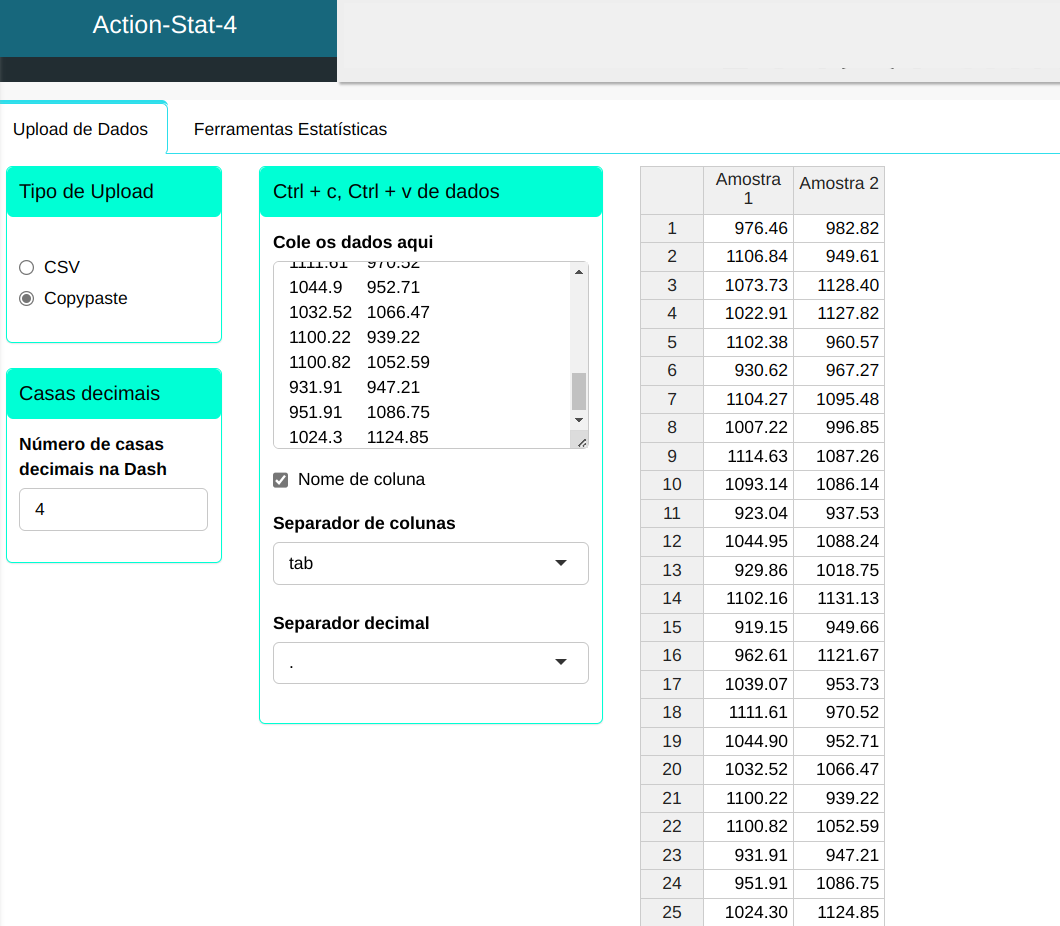
Para realizar o teste, configuramos conforme a figura abaixo.
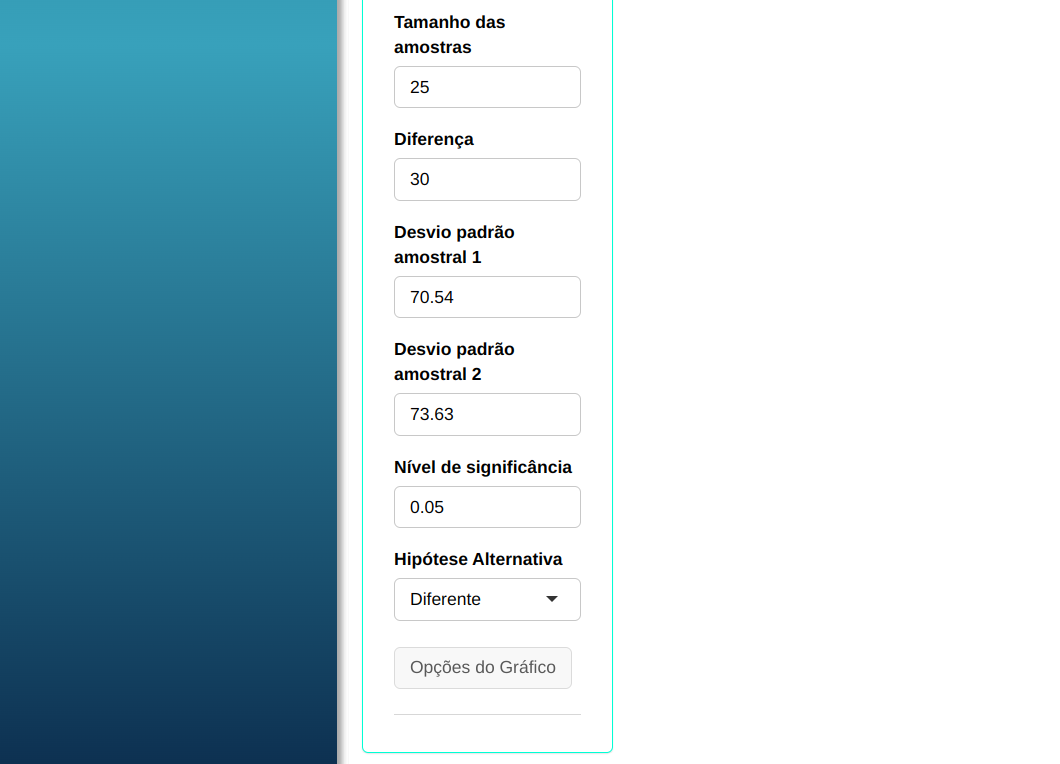
Clique em Calcular para obter os resultados. Também pode baixar os resultados no formato Word.

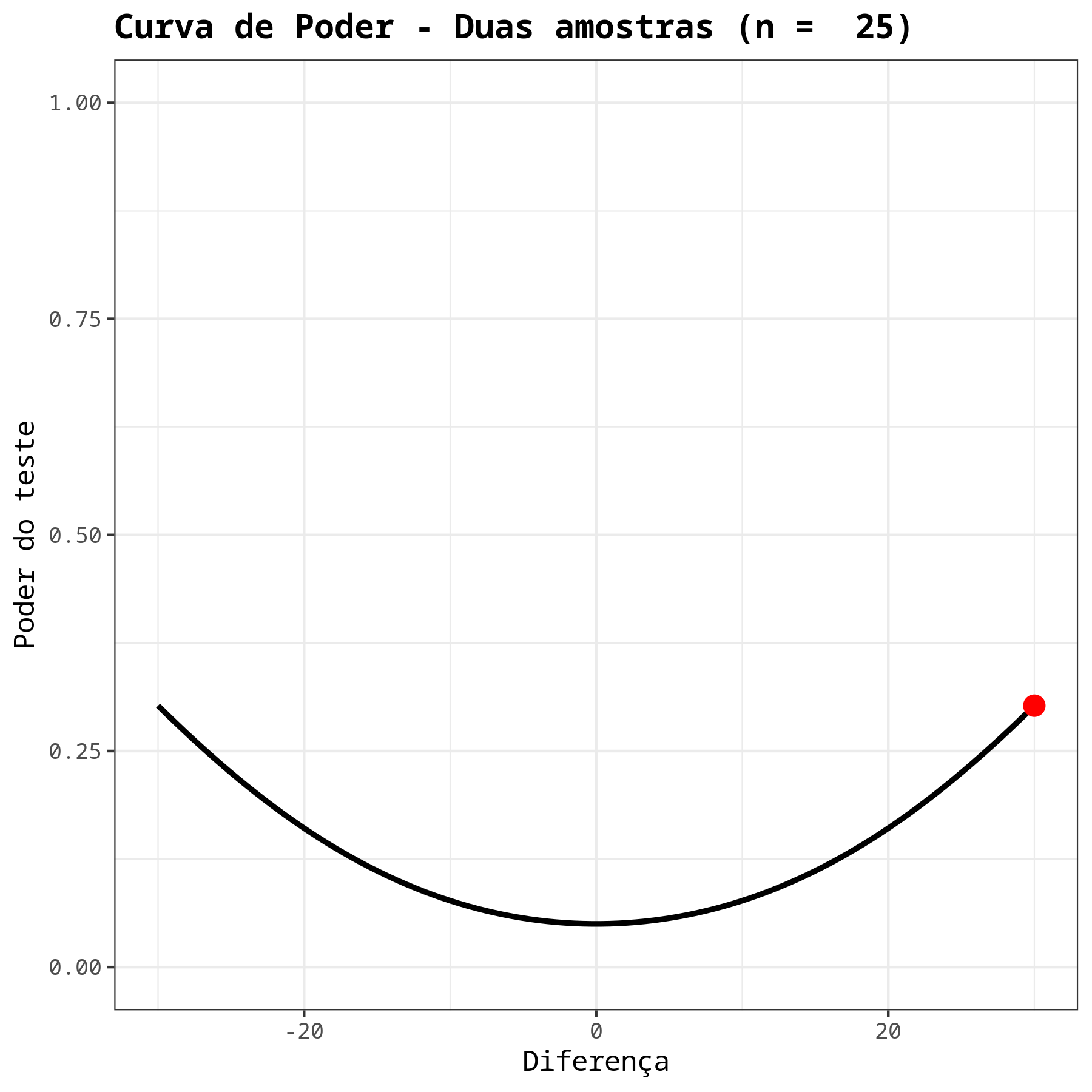
Os resultados são:
Teste T - Duas amostras (tamanhos iguais)
| V1 | |
|---|---|
| Poder | 0.302466 |
| Tamanho da amostra | 25 |
| Diferença | 30 |
| Desvio padrão 1 | 70.54 |
| Desvio padrão 2 | 73.63 |
| Nível de significância | 0.05 |
| Hipótese Alternativa | Diferente |
Exemplo 4:
Suponha agora, com o mesmo conjunto de dados, que queiramos calcular o tamanho amostral necessário para que se detecte uma diferença $\mu_1 - \mu_2 =$ 0,6 com um poder de, no mínimo, 0,9 e um desvio padrão de 1,40434.
| Amostra 1 | Amostra 2 |
|---|---|
| 976,46 | 982,82 |
| 1106,84 | 949,61 |
| 1073,73 | 1128,40 |
| 1022,91 | 1127,82 |
| 1102,38 | 960,57 |
| 930,62 | 967,27 |
| 1104,27 | 1095,48 |
| 1007,22 | 996,85 |
| 1114,63 | 1087,26 |
| 1093,14 | 1086,14 |
| 923,04 | 937,53 |
| 1044,95 | 1088,24 |
| 929,86 | 1018,75 |
| 1102,16 | 1131,13 |
| 919,15 | 949,66 |
| 962,61 | 1121,67 |
| 1039,07 | 953,73 |
| 1111,61 | 970,52 |
| 1044,90 | 952,71 |
| 1032,52 | 1066,47 |
| 1100,22 | 939,22 |
| 1100,82 | 1052,59 |
| 931,91 | 947,21 |
| 951,91 | 1086,75 |
| 1024,30 | 1124,85 |
| Poder | $\mathbf{\alpha}$ | Diferença $\mathbf{(\mu_1 - \mu_2)}$ | Desvio-Padrão sp | |
| $\quad$ 0,9 | 0,05 | $\qquad \quad$ 0,6 | $\quad \quad$ 1,40434 |

Realizaremos o teste e configuramos conforme a figura abaixo.
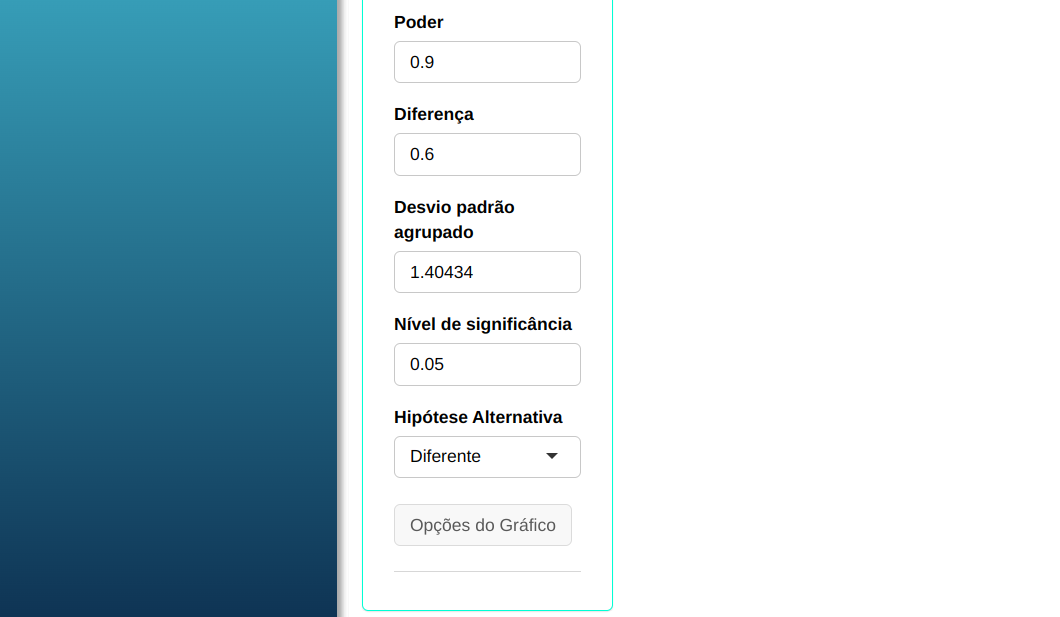
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.
Os resultados são:
Teste T - Duas amostras (tamanhos iguais)
| V1 | |
|---|---|
| Poder | 0.9 |
| Tamanho da amostra | 117 |
| Diferença | 0.6 |
| Desvio padrão | 1.40434 |
| Nível de significância | 0.05 |
| Hipótese Alternativa | Diferente |
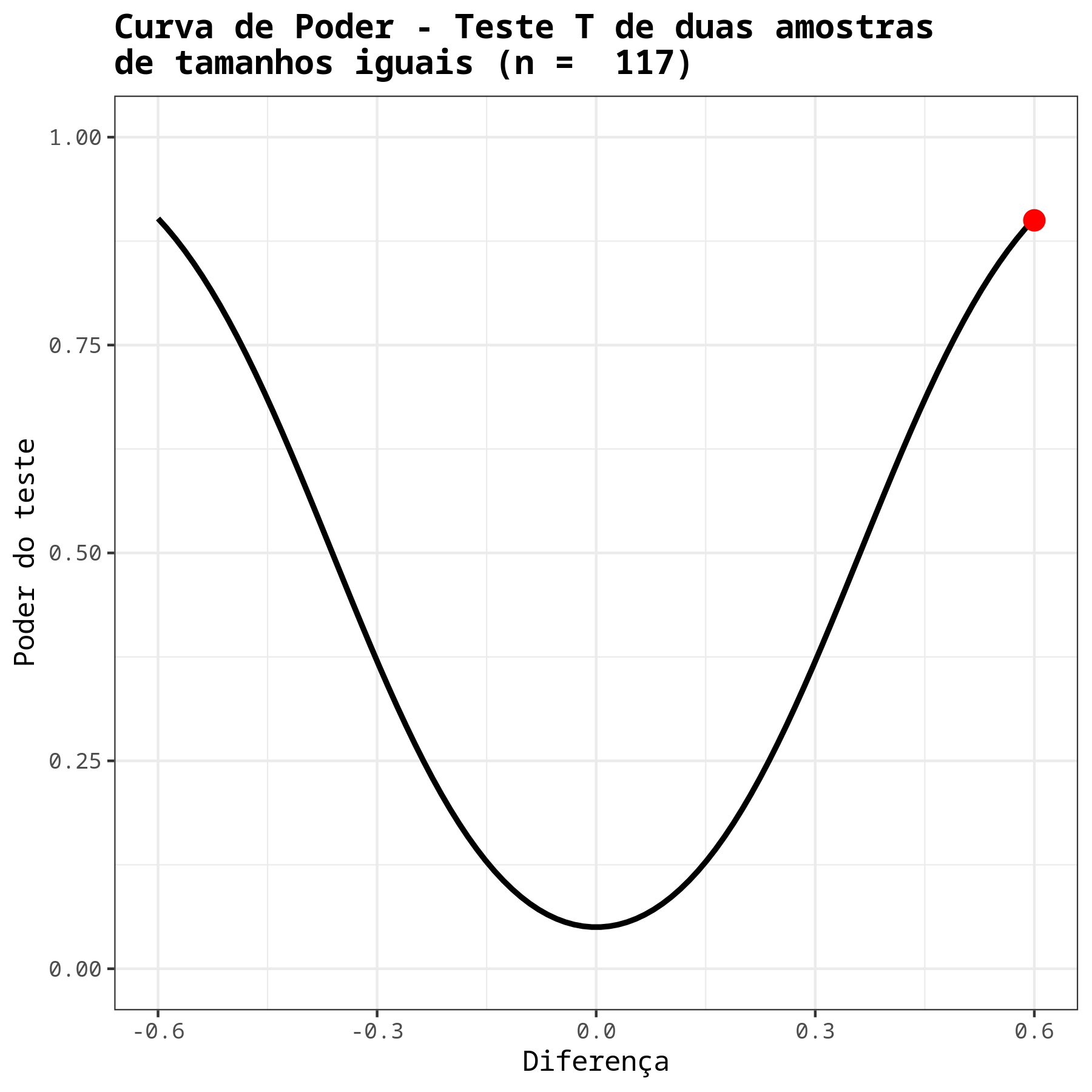
Concluímos então que, para detectar uma diferença de 0,6 com um poder de, no mínimo, 0,9, é necessário que as duas amostras tenham 117 elementos.
Exemplo 5:
Compare as médias das amostras cujas medições estão apresentadas na tabela a seguir.
| Dados | Amostra |
|---|---|
| 18,8 | Amostra 1 |
| 20,504 | Amostra 1 |
| 18,621 | Amostra 1 |
| 19,919 | Amostra 1 |
| 21,117 | Amostra 1 |
| 17,591 | Amostra 1 |
| 18,756 | Amostra 1 |
| 18,977 | Amostra 1 |
| 20,308 | Amostra 1 |
| 18,899 | Amostra 1 |
| 20,835 | Amostra 1 |
| 17,527 | Amostra 1 |
| 17,078 | Amostra 1 |
| 17,62 | Amostra 1 |
| 21,426 | Amostra 1 |
| 19,169 | Amostra 1 |
| 19,29 | Amostra 1 |
| 22,059 | Amostra 1 |
| 18,585 | Amostra 1 |
| 17,89 | Amostra 1 |
| 18,755 | Amostra 1 |
| 19,203 | Amostra 1 |
| 18,419 | Amostra 1 |
| 20,764 | Amostra 1 |
| 21,055 | Amostra 1 |
| 22,284 | Amostra 2 |
| 21,901 | Amostra 2 |
| 25,302 | Amostra 2 |
| 22,447 | Amostra 2 |
| 22,771 | Amostra 2 |
| 22,057 | Amostra 2 |
| 22,881 | Amostra 2 |
| 17,968 | Amostra 2 |
| 23,382 | Amostra 2 |
| 21,043 | Amostra 2 |
| 22,629 | Amostra 2 |
| 22,86 | Amostra 2 |
| 24,515 | Amostra 2 |
| 22,426 | Amostra 2 |
| 21,203 | Amostra 2 |
| 24,62 | Amostra 2 |
| 22,058 | Amostra 2 |
| 23,15 | Amostra 2 |
| 22,787 | Amostra 2 |
| 24,009 | Amostra 2 |
| 21,491 | Amostra 2 |
| 22,699 | Amostra 2 |
| 24,662 | Amostra 2 |
| 21,983 | Amostra 2 |
| 21,917 | Amostra 2 |
| 21,198 | Amostra 2 |
| 22,909 | Amostra 2 |
| 23,327 | Amostra 2 |
| 24,534 | Amostra 2 |
| 21,152 | Amostra 2 |
Estabelecer as hipóteses:
- $H_0$: $\mu_1 - \mu_2 = $ 0
- $H_1$: $\mu_1 - \mu_2 \neq $ 0
Primeiramente, é necessário calcular o desvio padrão. Utilizando a ferramenta Resumo descritivo do Action, obtêm-se os valores $s_1$ = 1,36228 e $s_2$ = 1,43822. Em seguida, deve-se calcular o poder do teste T de duas amostras em detectar uma diferença $\mu_1 - \mu_2 =$ 1,5.
| $\mathbf{n_1}$ | $\mathbf{n_2}$ | $\mathbf{\alpha}$ | Diferença $\mathbf{(\mu_1 - \mu_2)}$ | Desvio-Padrão 1 | Desvio-Padrão 2 |
| 25 | 30 | 0,05 | $\qquad \quad$ 1,5 | $\qquad$ 1,36228 | $\quad$ 1,43822 |
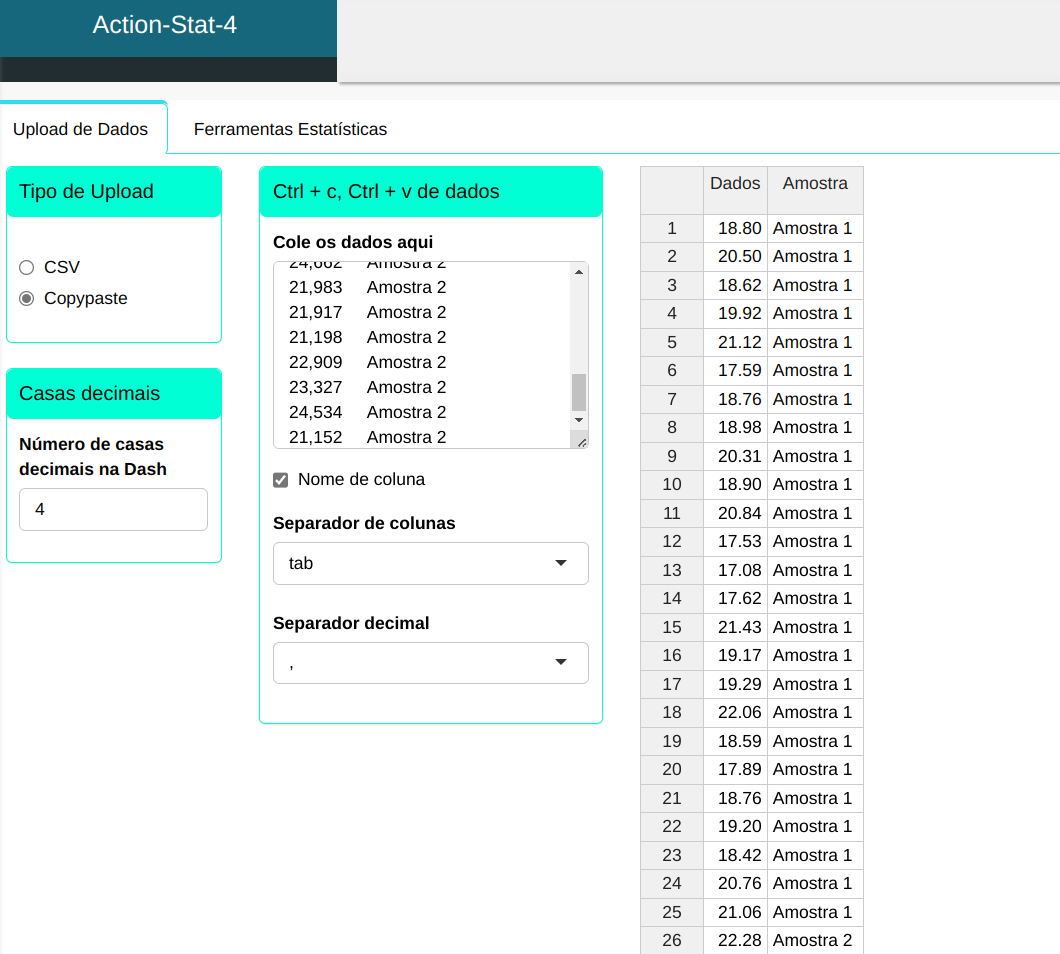
Realizaremos o teste e configuramos conforme a figura abaixo.
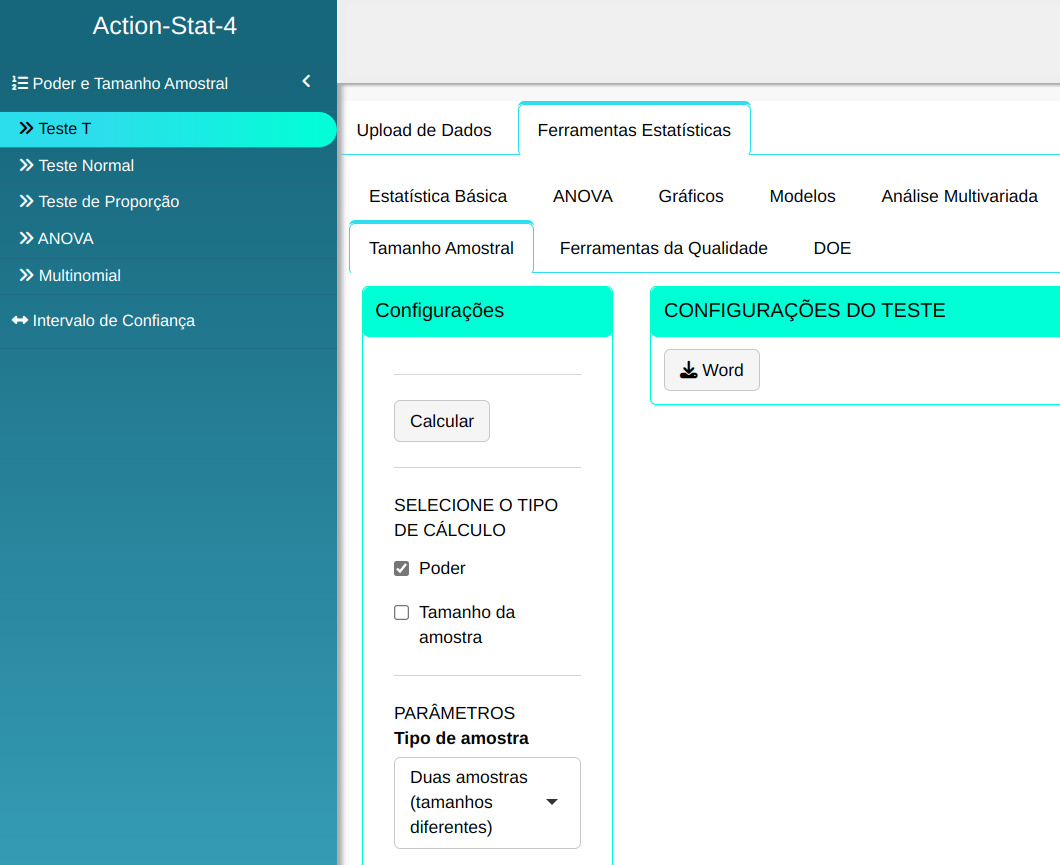
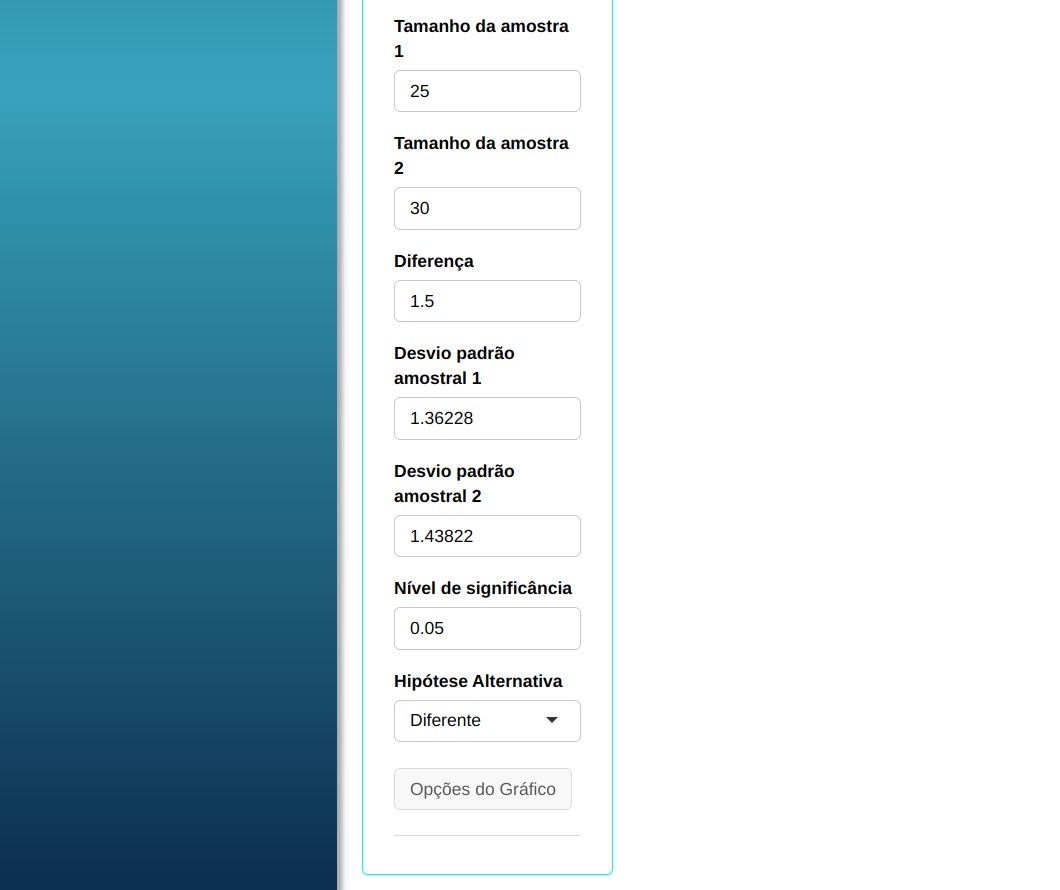
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Teste T - Duas amostras (tamanhos diferentes)
| V1 | |
|---|---|
| Poder | 0.9720551 |
| Tamanho da amostra 1 | 25 |
| Tamanho da amostra 2 | 30 |
| Diferença | 1.5 |
| Desvio padrão 1 | 1.36228 |
| Desvio padrão 2 | 1.43822 |
| Nível de significância | 0.05 |
| Hipótese Alternativa | Diferente |
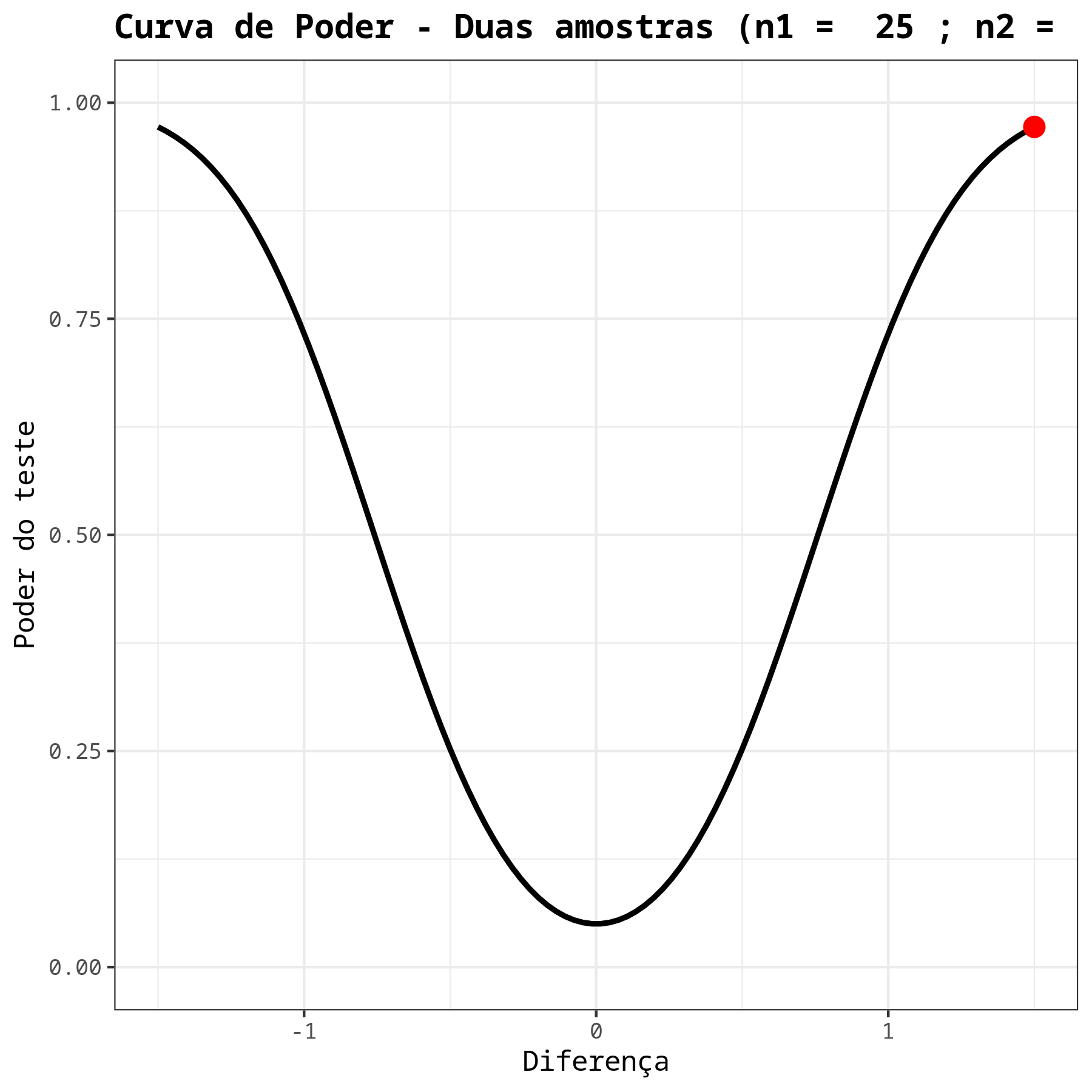
Ou seja, para detectar uma diferença d = 1,5 entre as médias, este teste apresenta um poder de 97,20%
Exemplo 6:
Considerando o exemplo anterior, suponha que, com uma amostra de tamanho 30 e desvio padrão agrupado de 1,40434, deseja-se calcular o tamanho da outra amostra necessário para que o teste T detecte uma diferença de 1,2 com poder de pelo menos 90%.
| Dados | Amostra |
|---|---|
| 18,8 | Amostra 1 |
| 20,504 | Amostra 1 |
| 18,621 | Amostra 1 |
| 19,919 | Amostra 1 |
| 21,117 | Amostra 1 |
| 17,591 | Amostra 1 |
| 18,756 | Amostra 1 |
| 18,977 | Amostra 1 |
| 20,308 | Amostra 1 |
| 18,899 | Amostra 1 |
| 20,835 | Amostra 1 |
| 17,527 | Amostra 1 |
| 17,078 | Amostra 1 |
| 17,62 | Amostra 1 |
| 21,426 | Amostra 1 |
| 19,169 | Amostra 1 |
| 19,29 | Amostra 1 |
| 22,059 | Amostra 1 |
| 18,585 | Amostra 1 |
| 17,89 | Amostra 1 |
| 18,755 | Amostra 1 |
| 19,203 | Amostra 1 |
| 18,419 | Amostra 1 |
| 20,764 | Amostra 1 |
| 21,055 | Amostra 1 |
| 22,284 | Amostra 2 |
| 21,901 | Amostra 2 |
| 25,302 | Amostra 2 |
| 22,447 | Amostra 2 |
| 22,771 | Amostra 2 |
| 22,057 | Amostra 2 |
| 22,881 | Amostra 2 |
| 17,968 | Amostra 2 |
| 23,382 | Amostra 2 |
| 21,043 | Amostra 2 |
| 22,629 | Amostra 2 |
| 22,86 | Amostra 2 |
| 24,515 | Amostra 2 |
| 22,426 | Amostra 2 |
| 21,203 | Amostra 2 |
| 24,62 | Amostra 2 |
| 22,058 | Amostra 2 |
| 23,15 | Amostra 2 |
| 22,787 | Amostra 2 |
| 24,009 | Amostra 2 |
| 21,491 | Amostra 2 |
| 22,699 | Amostra 2 |
| 24,662 | Amostra 2 |
| 21,983 | Amostra 2 |
| 21,917 | Amostra 2 |
| 21,198 | Amostra 2 |
| 22,909 | Amostra 2 |
| 23,327 | Amostra 2 |
| 24,534 | Amostra 2 |
| 21,152 | Amostra 2 |
| Poder | $\mathbf{\alpha}$ | Diferença $\mathbf{(\mu_1 - \mu_2)}$ | Desvio-Padrão sp | |
| $\quad$ 0,9 | 0,05 | $\qquad \quad$ 1,2 | $\quad \quad$ 1,40434 |

Para realizar o teste, configuramos conforme a figura abaixo.
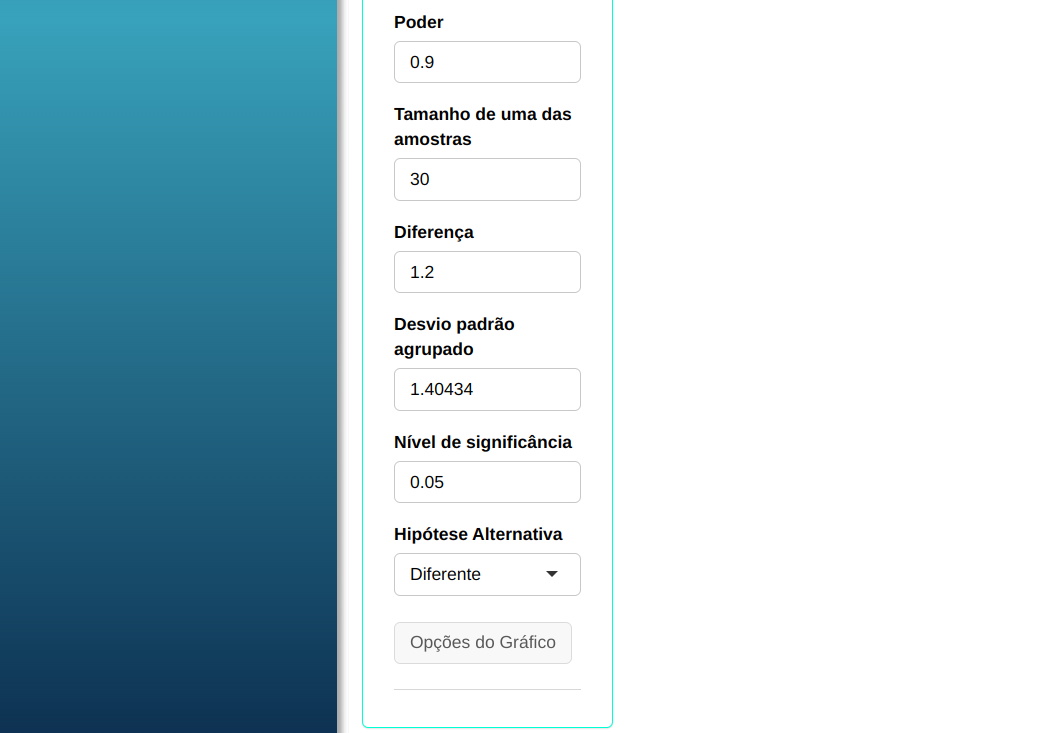
Clique em Calcular para obter os resultados. Também pode baixar os resultados no formato Word.
Os resultados são:
Teste T - Duas amostras (tamanhos diferentes)
| V1 | |
|---|---|
| Poder | 0.9 |
| Tamanho da amostra 1 | 30 |
| Tamanho da amostra 2 | 30 |
| Diferença | 1.2 |
| Desvio padrão | 1.40434 |
| Nível de significância | 0.05 |
| Hipótese Alternativa | Diferente |
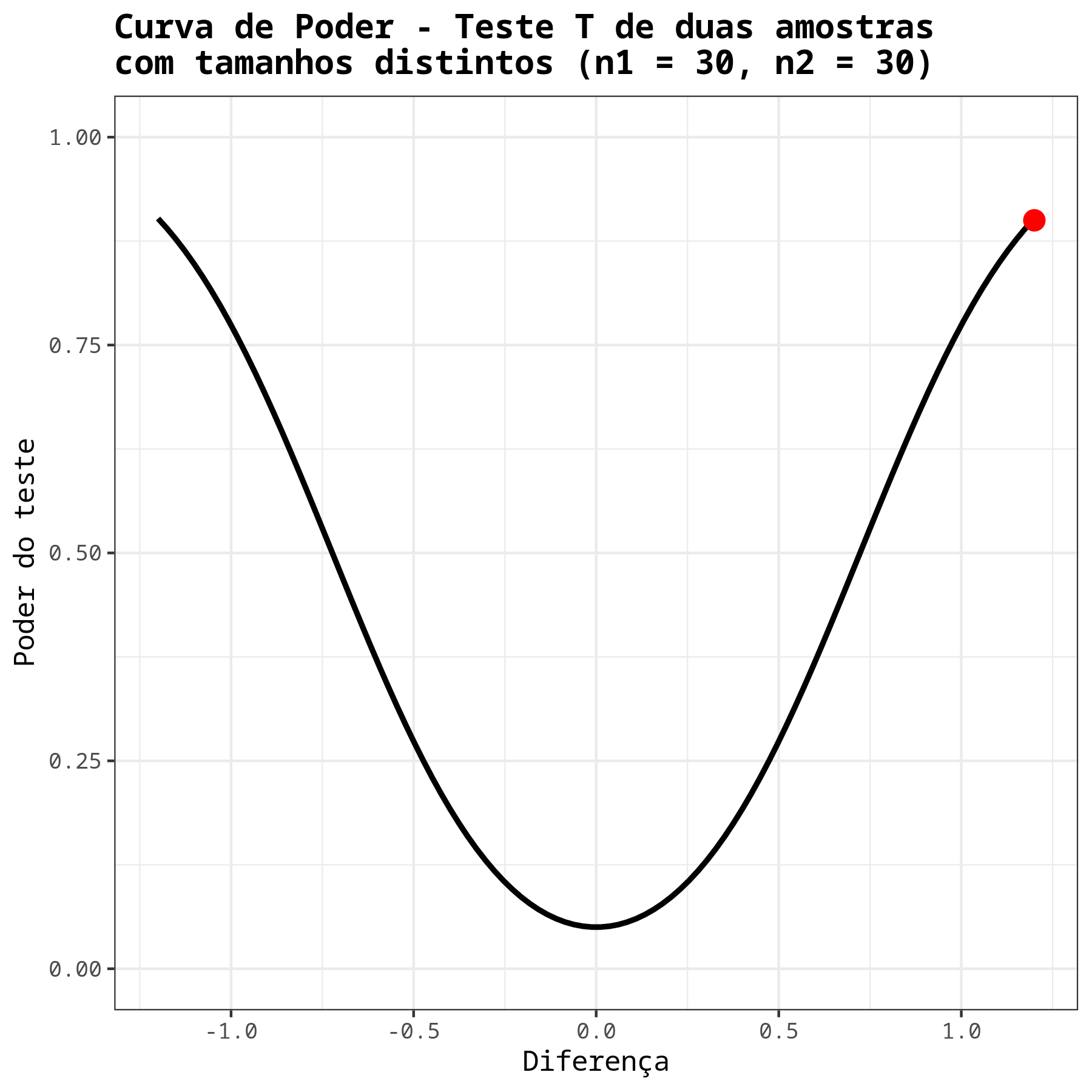
Concluímos então que, com uma das amostras com 30 elementos, para detectar uma diferença de 1,2 com um poder de, no mínimo, 90%, é necessário que a outra amostra também tenha aproximadamente 30 elementos.
Exemplo 7:
Consideremos $X_1,X_2,\ldots, X_{20}$ uma amostra de medições do laboratório da Empresa A e $Y_1,Y_2, \dots , Y_{20} $ uma amostra de miedições do laboratório da Empresa B. Os testes dos dois laboratórios são realizadas no mesmo padrão, por isso, existe uma correlação entre eles, ou seja, as amostras são dependentes. Avalie a compatibilidade das medições entre o laboratório da empresa A e do laboratório da empresa B.
| Laboratório da empresa A (Xi) | Laboratório da empresa B (Yi) | Diferença (Di) |
|---|---|---|
| 1,00552 | 0,01942 | 0,98610 |
| -1,49928 | -0,46512 | -1,03416 |
| 0,21367 | 0,53218 | -0,31851 |
| 0,44658 | -0,14844 | 0,59502 |
| 0,62766 | -0,60021 | 1,22787 |
| 0,31091 | 0,06495 | 0,24596 |
| -0,83878 | 0,33013 | -1,16891 |
| -0,29054 | 0,12116 | -0,41170 |
| -0,08487 | 0,74269 | -0,82756 |
| -1,26465 | -1,64232 | 0,37767 |
| -0,06353 | 0,05497 | -0,11850 |
| -1,07632 | 0,76342 | -1,83974 |
| -1,34134 | 1,74131 | -3,08265 |
| -0,55062 | -0,06392 | -0,48670 |
| 1,61848 | -1,88146 | 3,49994 |
| 0,50997 | -0,76135 | 1,27132 |
| 0,76027 | -0,23009 | 0,99036 |
| 0,68061 | -1,16800 | 1,84861 |
| -1,91464 | 0,88392 | -2,79856 |
| -0,20072 | 0,96512 | -1,16584 |
Então, considerando Di = Xi - Yi e estabelecendo as hipóteses
- $H_0: \mu_D =$ 0
- $H_0: \mu_D \neq $ 0
onde $\mu_D$ será estimado pela média amostral das diferenças, ou seja, D. Utilizando a ferramenta Estatística Básica do Action, temos que a média amostral é D = -0,110499 e o desvio padrão amostral é S = 1,56907778
Faremos o upload dos dados no sistema.
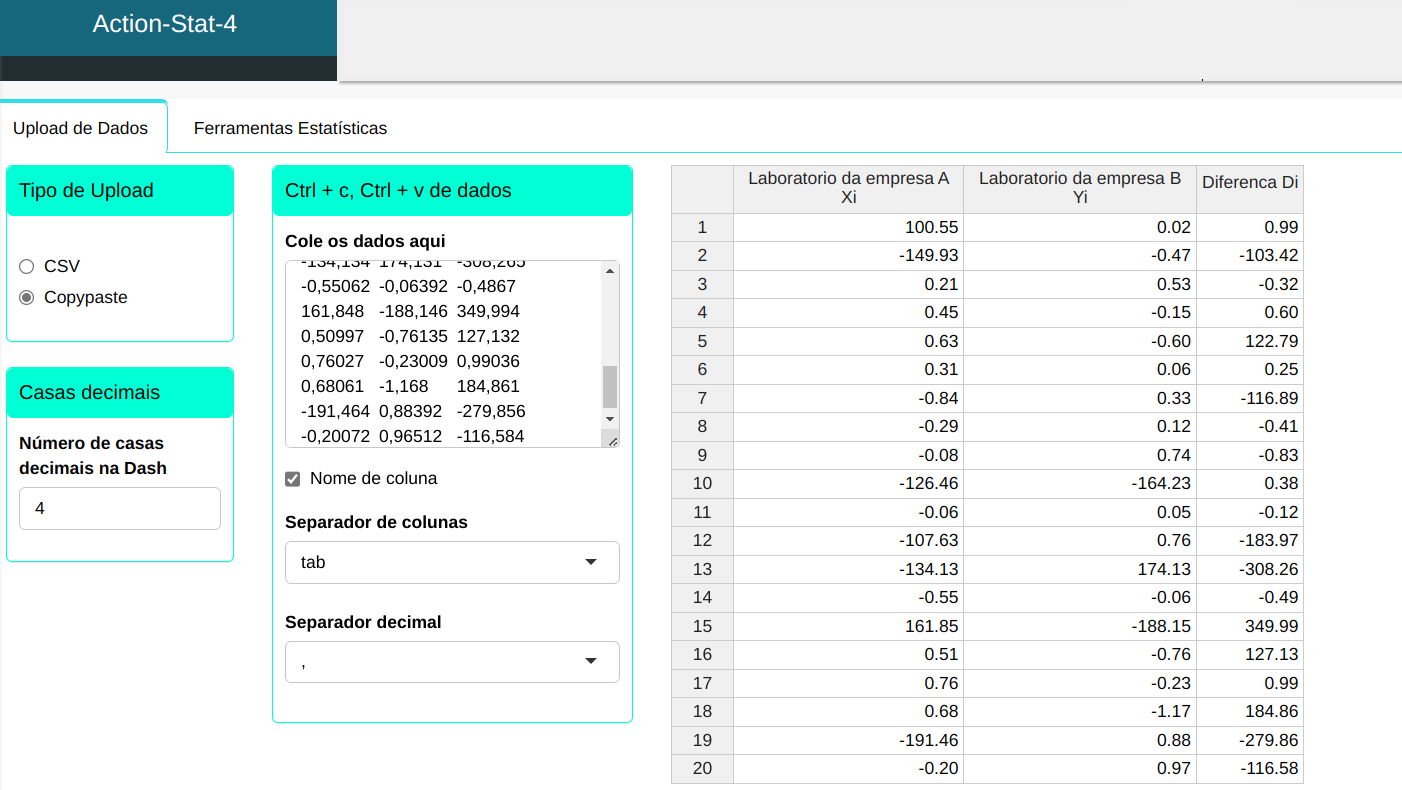
Para realizar o teste, configuramos conforme a figura abaixo.
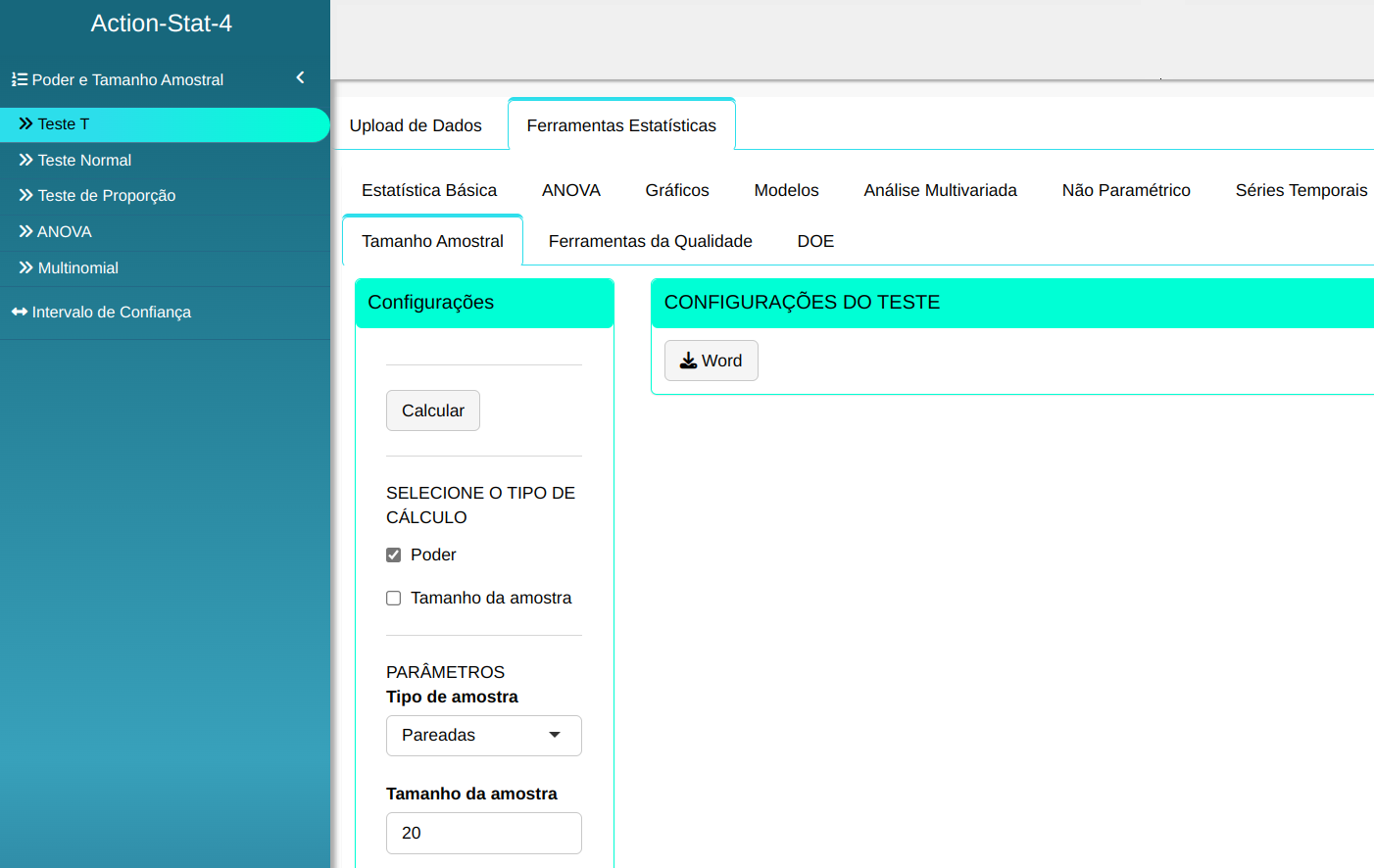
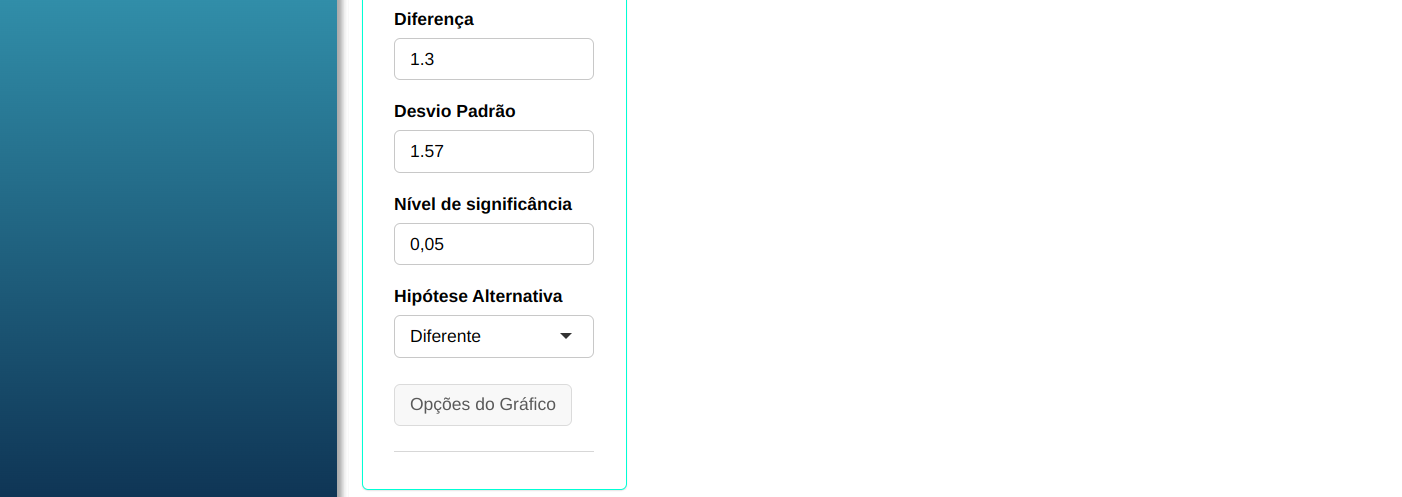
Clique em Calcular para obter os resultados. Também pode baixar os resultados no formato Word.

Os resultados são:
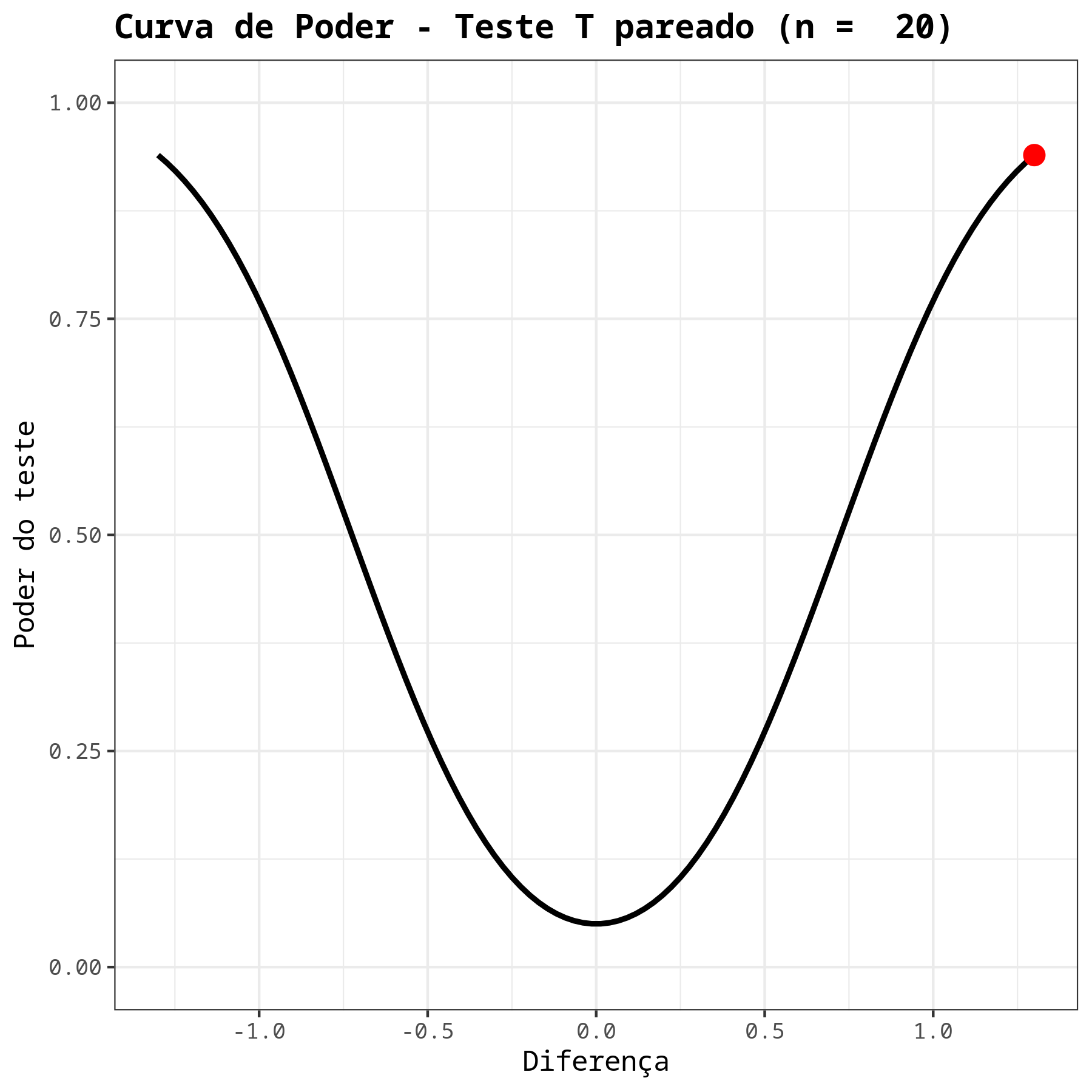
Teste T - Pareado
| V1 | |
|---|---|
| Poder | 0.9394575 |
| Tamanho da amostra | 20 |
| Diferença | 1.3 |
| Nível de significância | 0.05 |
| Desvio padrão | 1.57 |
| Hipótese Alternativa | Diferente |
Exemplo 8:
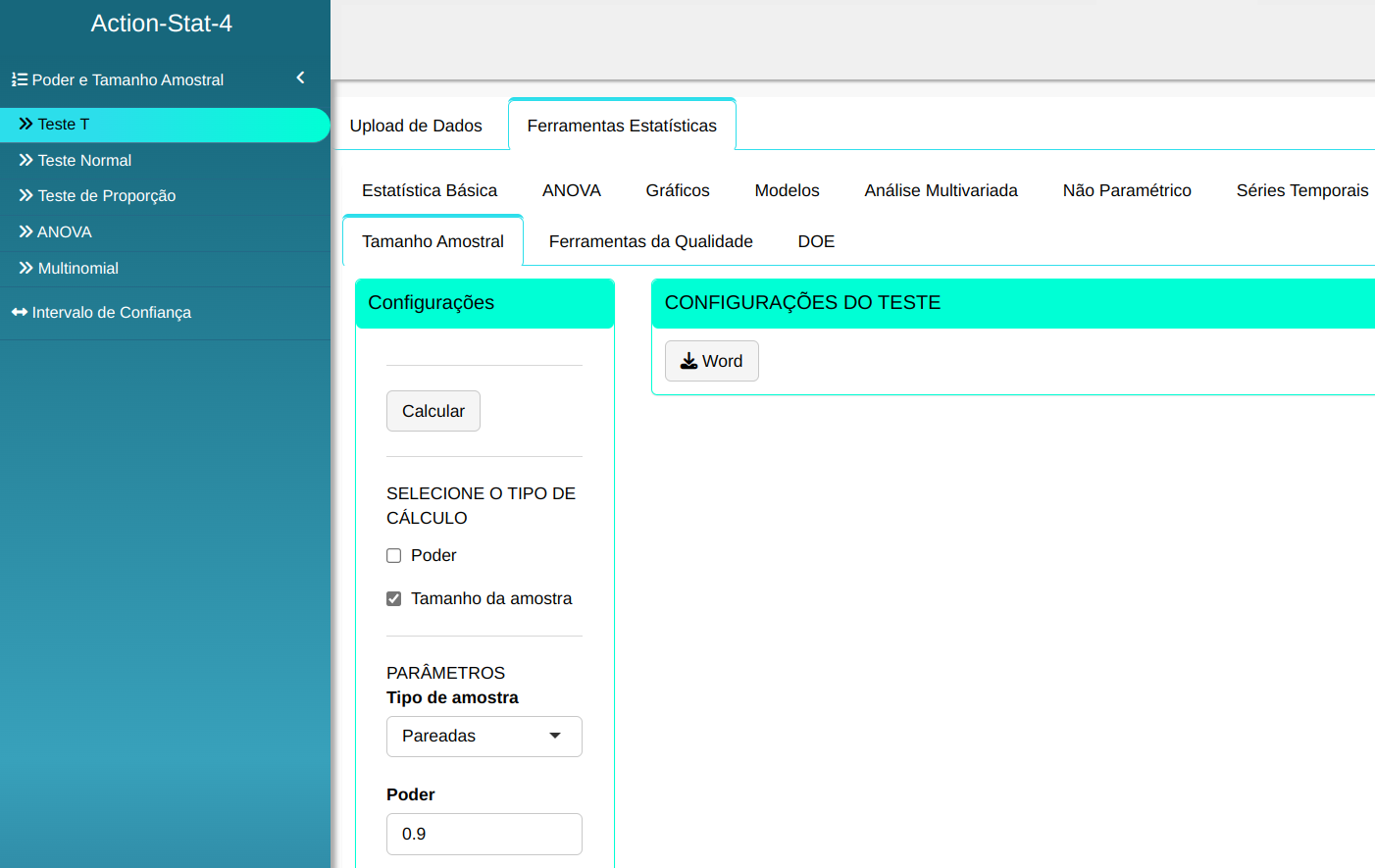
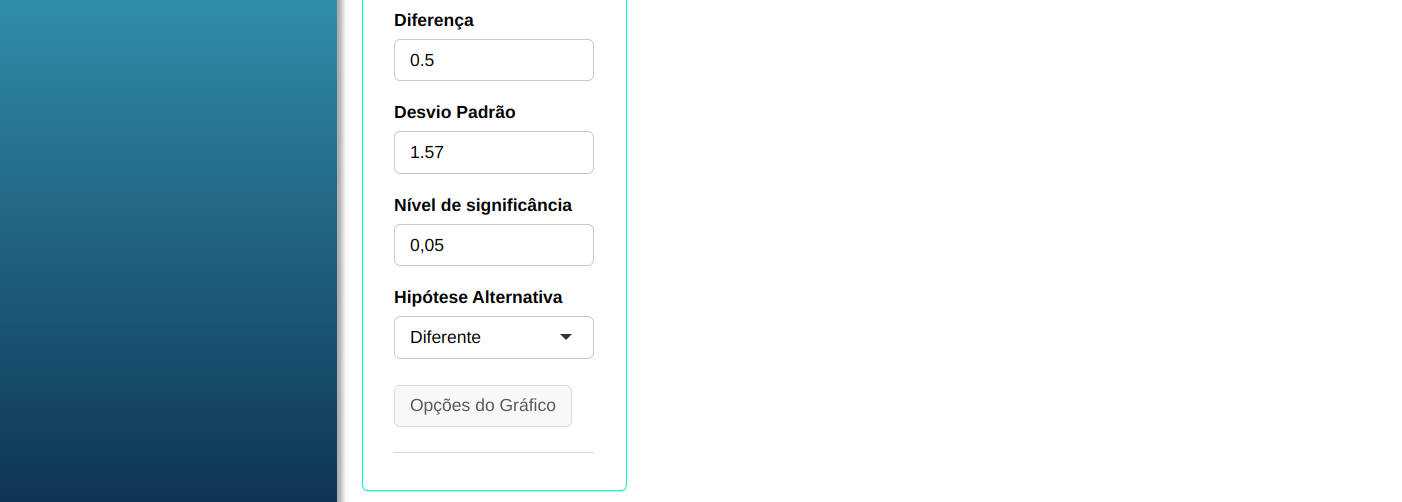
Usando o exemplo anterior, suponha agora que queremos calcular o tamanho amostral necessário para que o teste T Pareado detecte uma diferença de 0,5 com um poder de, no mínimo, 90%.
| Laboratório da empresa A (Xi) | Laboratório da empresa B (Yi) | Diferença (Di) |
|---|---|---|
| 1,00552 | 0,01942 | 0,98610 |
| -1,49928 | -0,46512 | -1,03416 |
| 0,21367 | 0,53218 | -0,31851 |
| 0,44658 | -0,14844 | 0,59502 |
| 0,62766 | -0,60021 | 1,22787 |
| 0,31091 | 0,06495 | 0,24596 |
| -0,83878 | 0,33013 | -1,16891 |
| -0,29054 | 0,12116 | -0,41170 |
| -0,08487 | 0,74269 | -0,82756 |
| -1,26465 | -1,64232 | 0,37767 |
| -0,06353 | 0,05497 | -0,11850 |
| -1,07632 | 0,76342 | -1,83974 |
| -1,34134 | 1,74131 | -3,08265 |
| -0,55062 | -0,06392 | -0,48670 |
| 1,61848 | -1,88146 | 3,49994 |
| 0,50997 | -0,76135 | 1,27132 |
| 0,76027 | -0,23009 | 0,99036 |
| 0,68061 | -1,16800 | 1,84861 |
| -1,91464 | 0,88392 | -2,79856 |
| -0,20072 | 0,96512 | -1,16584 |

Para realizar o teste, configuramos conforme a figura abaixo.
Clique em Calcular para obter os resultados. Também pode baixar os resultados no formato Word.
Os resultados são:
Teste T - Pareado
| V1 | |
|---|---|
| Poder | 0.9 |
| Tamanho da amostra | 106 |
| Diferença | 0.5 |
| Desvio padrão | 1.57 |
| Nível de significância | 0.05 |
| Hipótese Alternativa | Diferente |
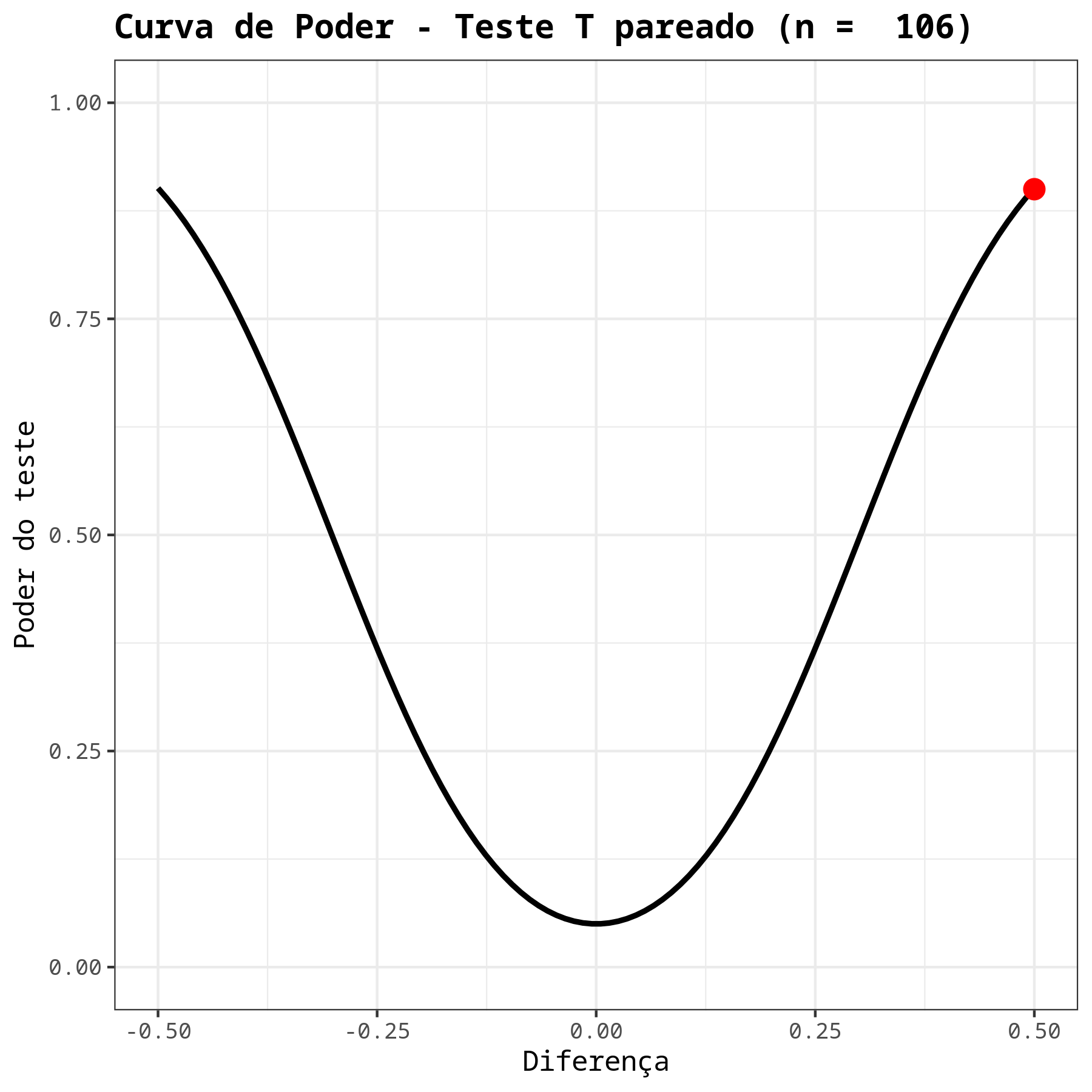
Portanto, para que o teste detecte uma diferença 0,5 no teste de hipóteses com um poder de, no mínimo 0,9 é necessário um tamanho amostral de, no mínimo, n = 106.