6. Validación de Limpieza
En algunas aplicaciones, estamos interesados en evaluar la capacidad de un proceso en el que solo observamos si el producto está dentro o fuera presupuesto.
Ejemplo:
En una industria farmacéutica, existe interés en evaluar el desempeño y la estabilidad de la cantidad de residuos después de la limpieza del equipo. El equipo que mide residuos detecta valores superiores a LD = 0.02348 y puede cuantificar valores por encima de LQ = 0.07862. El límite superior de especificación para este caso es LSE = 0.18.
| LI | LS |
|---|---|
| 0.08002 | 0.08002 |
| 0.14927 | 0.14927 |
| 0.02348 | 0.07862 |
| 0.02348 | 0.07862 |
| 0.02348 | 0.07862 |
| 0.02348 | 0.07862 |
| 0.02348 | 0.07862 |
| 0.02348 | 0.07862 |
| 0.08777 | 0.08777 |
| 0.09848 | 0.09848 |
| 0.15716 | 0.15716 |
| 0.09648 | 0.09648 |
| 0.07 | 0.07 |
| 0.25 | 0.25 |
| 0.11 | 0.11 |
| 0.13 | 0.13 |
| 0.06 | 0.06 |
| 0.06 | 0.06 |
| 0 | 0.02348 |
| 0 | 0.02348 |
| 0 | 0.02348 |
Subiremos los datos al sistema.
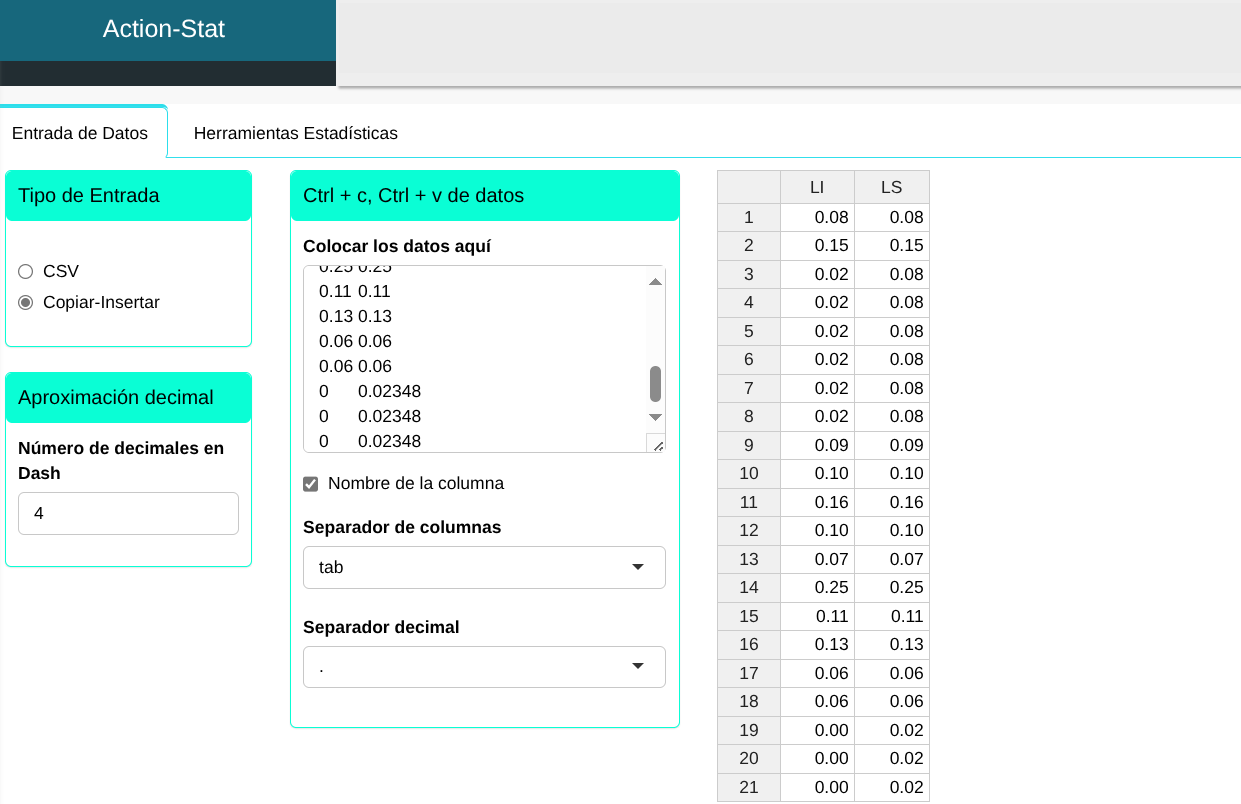
Realizaremos el análisis, y configuramos conforme la figura abajo.
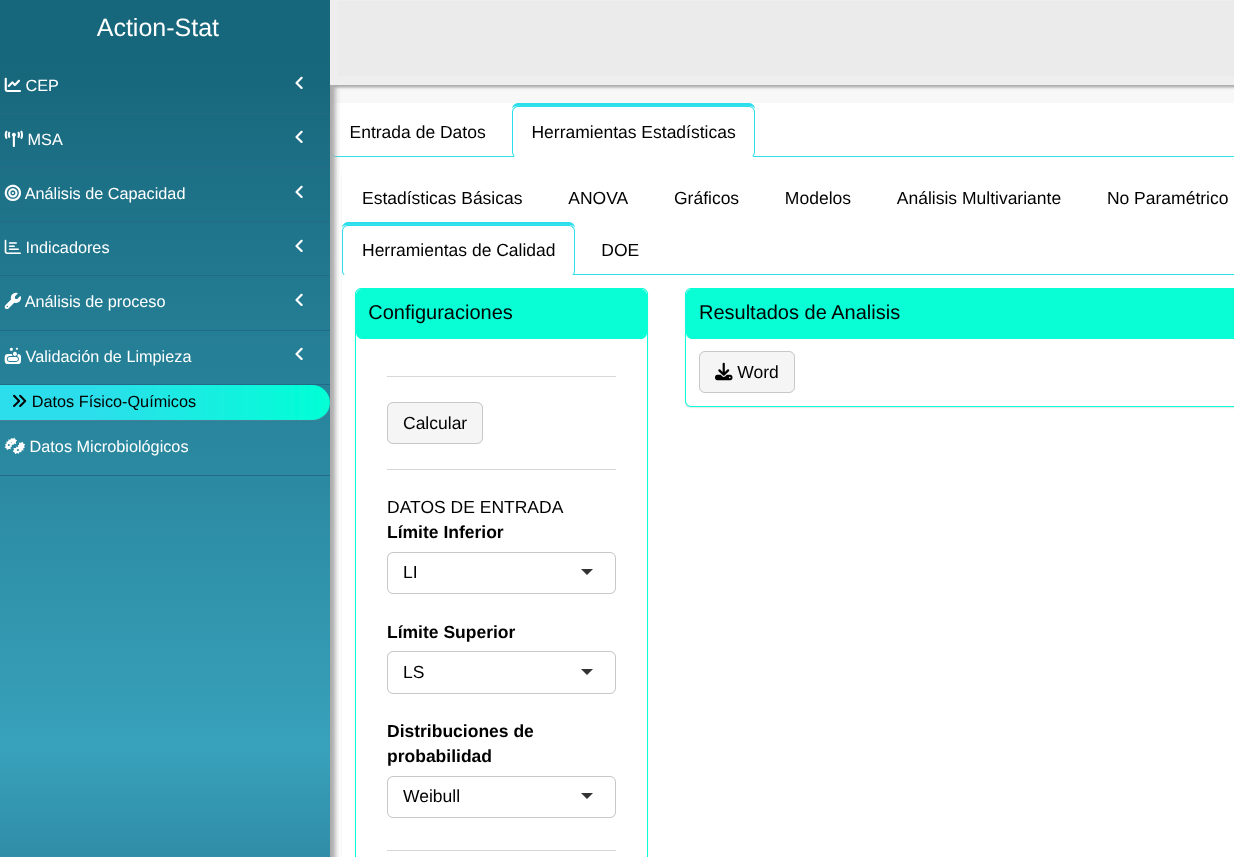
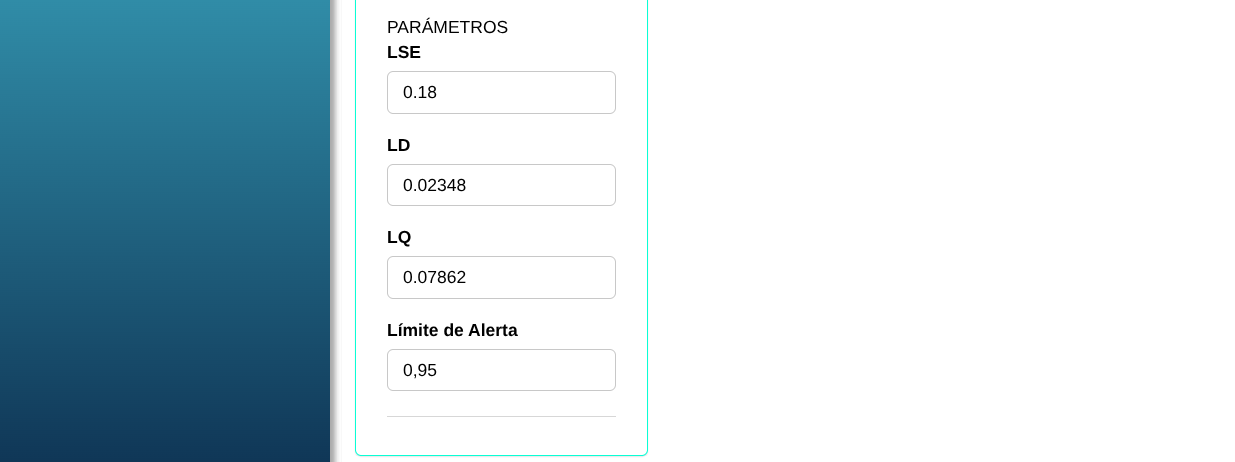
En seguida, haga un clic en calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.
Los resultados son:
ESPECIFICACIONES
| Valor | |
|---|---|
| Muestra | 21 |
| Límite superior de Especificación | 0.18 |
| Límite de Detección | 0.02348 |
| Límite de Cuantificación | 0.07862 |
MÉTODO DE ESTIMACIÓN
| $\qquad$ Método | Distribución de probabilidad |
| Método de máxima verosimilitud | $\qquad \qquad$ Weibull |
ESTIMACIÓN DEL COEFICIENTE
| Parámetro | Estimativa | Error estándar | Límite inferior | Límite superior |
|---|---|---|---|---|
| shape | 1.487 | 0.2722 | 0.9534 | 2.02 |
| scala | 0.089 | 0.0141 | 0.0615 | 0.117 |
CUANTILES
| Percentil | Cuantil | Error estándar | Límite inferior | Límite superior | |
|---|---|---|---|---|---|
| 1 | 0.1 | 0.02 | 0.007 | 0.006 | 0.034 |
| 2 | 0.2 | 0.033 | 0.008 | 0.014 | 0.051 |
| 3 | 0.3 | 0.045 | 0.011 | 0.024 | 0.065 |
| 4 | 0.4 | 0.057 | 0.012 | 0.034 | 0.079 |
| 5 | 0.5 | 0.07 | 0.013 | 0.045 | 0.094 |
| 6 | 0.6 | 0.084 | 0.014 | 0.057 | 0.111 |
| 7 | 0.7 | 0.101 | 0.015 | 0.071 | 0.131 |
| 8 | 0.8 | 0.123 | 0.018 | 0.087 | 0.158 |
| 9 | 0.9 | 0.156 | 0.024 | 0.109 | 0.204 |
| 10 | 0.95 | 0.187 | 0.031 | 0.125 | 0.248 |
| 11 | 0.96 | 0.196 | 0.034 | 0.13 | 0.262 |
| 12 | 0.97 | 0.207 | 0.037 | 0.135 | 0.279 |
| 13 | 0.98 | 0.233 | 0.041 | 0.142 | 0.304 |
| 14 | 0.99 | 0.249 | 0.049 | 0.153 | 0.345 |
| 15 | 0.999 | 0.318 | 0.073 | 0.175 | 0.46 |
| 16 | 0.95 | 0.187 | 0.031 | 0.125 | 0.248 |
ÍNDICE DE RENDIMIENTO
| Parámetro | Valor | |
|---|---|---|
| 1 | PpK | 0.444990381722115 |
| 2 | PPM | 58378.0132293608 |
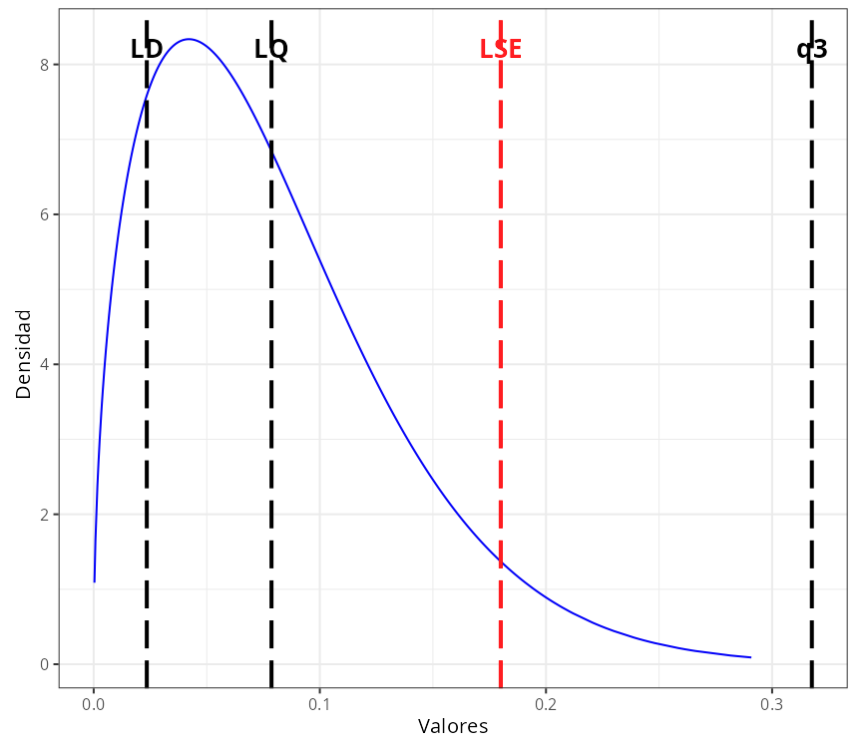
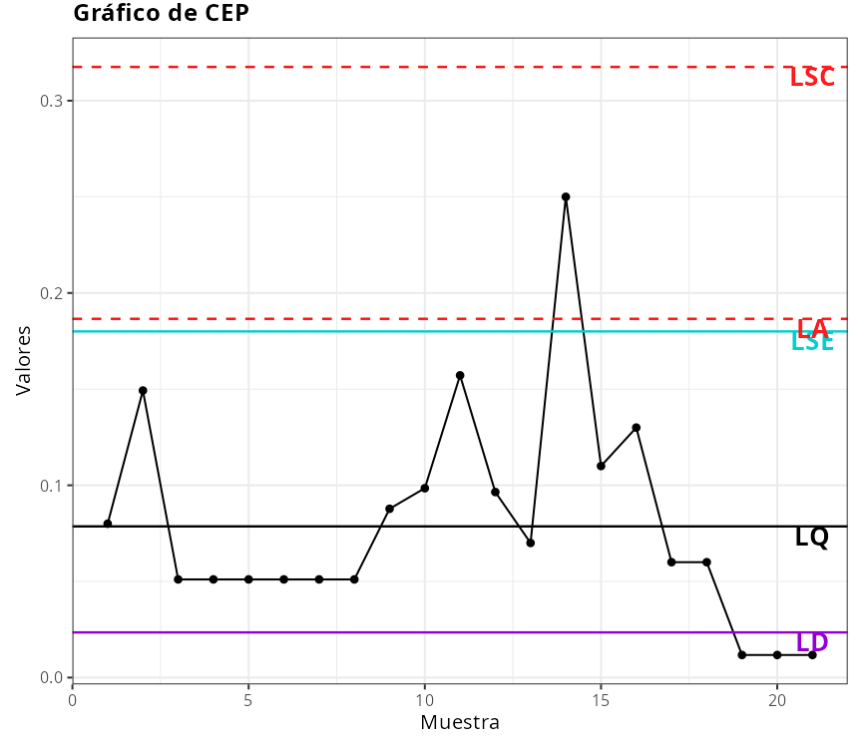
Límite de Control
| 1 | Límite de Alerta | 0.186544150929521 |
| 2 | Límite Superior de control | 0.317566810277244 |