1. ANOVA Efecto Fijo
El ANOVA se utiliza para analizar el comportamiento de varios tratamientos de un factor aplicado al proceso y/o al producto.
Ejemplo 1:
Consideremos un proceso, producto o servicio en el que queremos evaluar el impacto del factor A, tal que A tiene k niveles, y estos niveles son fijos. Supongamos que se selecciona una muestra de N unidades experimentales completamente al azar a partir de una población de unidades experimentales. La unidad experimental es la unidad básica a la que se aplican los tratamientos.
| Factor | Resistencia |
|---|---|
| 15 | 7 |
| 15 | 7 |
| 15 | 15 |
| 15 | 11 |
| 15 | 9 |
| 20 | 12 |
| 20 | 17 |
| 20 | 12 |
| 20 | 18 |
| 20 | 18 |
| 25 | 14 |
| 25 | 18 |
| 25 | 18 |
| 25 | 19 |
| 25 | 19 |
| 30 | 19 |
| 30 | 25 |
| 30 | 22 |
| 30 | 19 |
| 30 | 23 |
| 35 | 7 |
| 35 | 10 |
| 35 | 11 |
| 35 | 15 |
| 35 | 11 |
Realizaremos el ANOVA de efectos fijos.
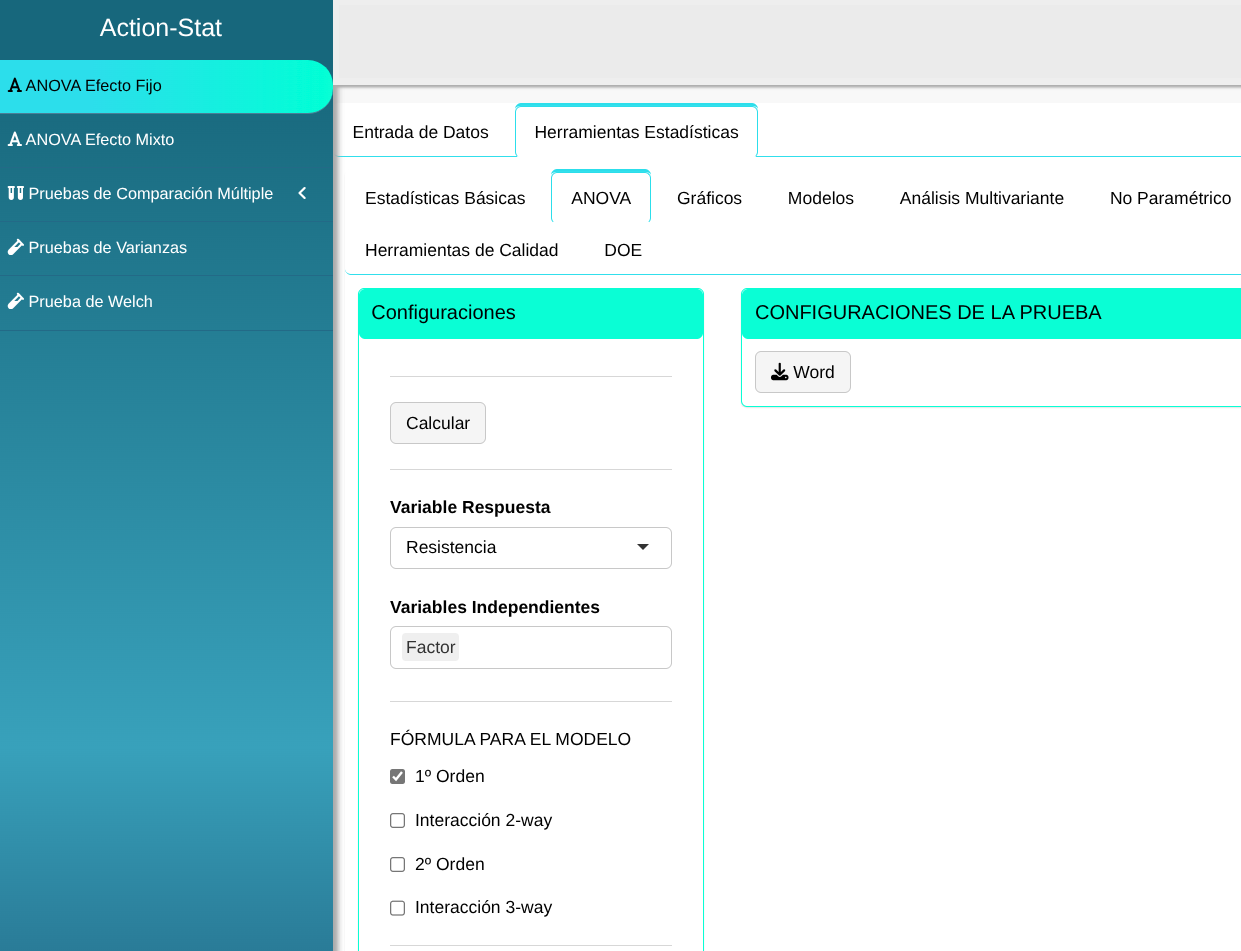
En seguida, haga un clic en Calcular para obtener los resultados. También es posible generar los análisis y descargar en el formato Word.

Los resultados son:
Cuadro ANOVA
| G.L. | Suma de Cuadrados | Cuadrado Medio | Estad. F | P-valor | |
|---|---|---|---|---|---|
| Factor | 4 | 475.76 | 118.94 | 14.757 | 0 |
| Residuos | 20 | 161.20 | 8.06 |
Intervalo de confianza del Efecto Factor
| Nivel | Límite Inferior | Efecto para media | Limite Superior |
|---|---|---|---|
| 15 | 7.152 | 9.8 | 12.448 |
| 20 | 12.752 | 15.4 | 18.048 |
| 25 | 14.952 | 17.6 | 20.248 |
| 30 | 18.952 | 21.6 | 24.248 |
| 35 | 8.152 | 10.8 | 13.448 |
Prueba de la Normalidad
| Valor | |
|---|---|
| Media | 0.000 |
| Desviación Estándar | 2.592 |
| N | 25.000 |
| Anderson-Darling | 0.519 |
| P-Valor | 0.170 |
En este ejemplo, la Suma de Cuadrados del Factor (475,76) es mucho mayor que la Suma de Cuadrados del Error (161,20), lo que ya indica que las medias no son iguales.
Si el valor P es inferior o igual al nivel de significación predeterminado ($\alpha$), significa que las medias de los niveles son diferentes. En caso contrario, son iguales. En este caso, como es inferior a 0,05, rechazamos la hipótesis nula de que las medias son iguales, es decir, podemos afirmar que las medias de los niveles son diferentes.
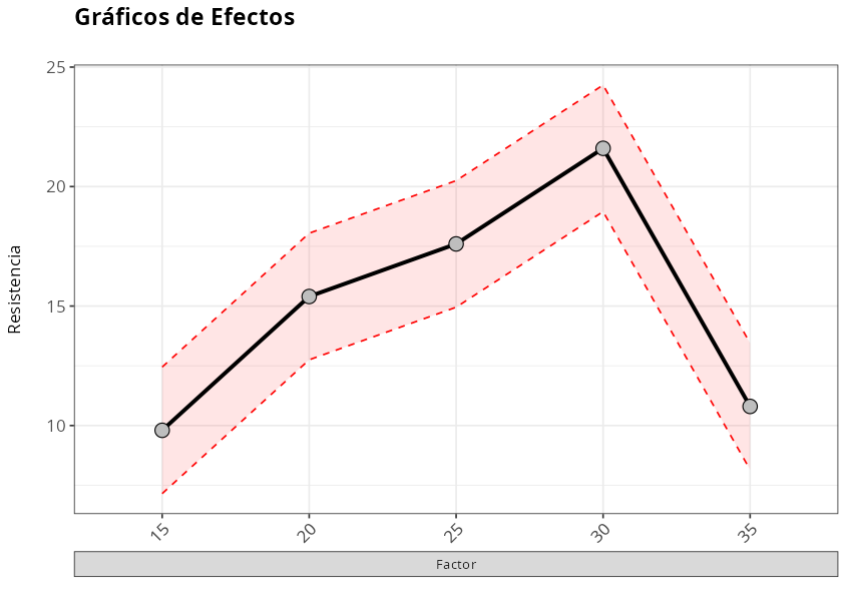
En el gráfico de efectos, los puntos negros son las medias de cada nivel de factor, que en la tabla se denominan Efectos.
Las líneas rojas representan el intervalo de confianza para las medias de los niveles de los factores.
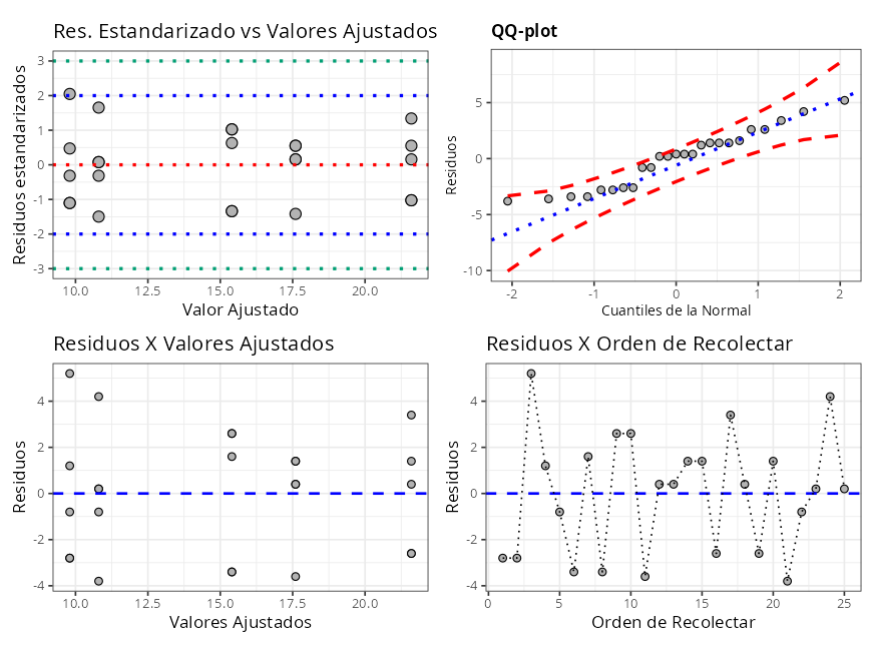
El gráfico 1: Gráfico de residuos estandarizados versus valores ajustados.
El gráfico 2: Gráfico de Residuales versus los Cuantiles Normales.
El gráfico 3: Gráfico de residuos versus los valores ajustados.
El Gráfico 4: Gráfico de Residuales versus a Orden de colecta, utilizando este gráfico para comprobar si los residuales son independientes. El criterio para el análisis es: si los puntos del gráfico se distribuyen aleatoriamente, esto indica independencia, por otro lado si muestran un patrón, esto indica dependencia en los residuales. En nuestro caso, es comprobado la independencia de los residuos.
En nuestro caso, se utiliza la prueba de Anderson-Darling, en la que la hipótesis nula es la normalidad de los datos y, mediante el ejemplo, comprobamos que no rechazamos ("aceptamos") la hipótesis nula y verificamos así la normalidad de los residuos.
Ejemplo 2:
Una empresa que produce limpiaparabrisas para automóviles desea saber cómo los factores Tipo de Caja Reductora y Tipo de Eje, utilizados en la fabricación de los motores que accionan los limpiaparabrisas, influyen en el ruido que se produce cuando se utilizan. Para ello, realizamos un experimento con 54 motores, con 3 tipos de Eje (Laminado, Cortado e Importado) y 2 tipos de Caja Reductora (Nacional e Importada). Para cada motor (unidad experimental) medimos el ruido. Los datos están en la siguiente tabla.
| Eje | Caja Reductora | Ruido |
|---|---|---|
| Rolado | Importado | 39,6 |
| Rolado | Nacional | 42,1 |
| Importado | Nacional | 40,9 |
| Cortado | Nacional | 38,2 |
| Rolado | Nacional | 42,0 |
| Cortado | Importado | 41,3 |
| Importado | Importado | 39,6 |
| Rolado | Nacional | 40,3 |
| Importado | Nacional | 40,7 |
| Importado | Importado | 36,9 |
| Rolado | Importado | 40,2 |
| Cortado | Importado | 46,8 |
| Cortado | Importado | 40,3 |
| Cortado | Nacional | 37,4 |
| Cortado | Nacional | 37,0 |
| Rolado | Importado | 48,4 |
| Importado | Importado | 39,9 |
| Importado | Nacional | 39,4 |
| Rolado | Importado | 40,9 |
| Rolado | Nacional | 38,9 |
| Cortado | Importado | 40,5 |
| Cortado | Nacional | 42,3 |
| Importado | Importado | 38,1 |
| Importado | Importado | 38,0 |
| Importado | Importado | 36,2 |
| Rolado | Importado | 41,0 |
| Cortado | Importado | 39,9 |
| Rolado | Importado | 41,0 |
| Cortado | Nacional | 41,3 |
| Importado | Nacional | 42,0 |
| Cortado | Importado | 39,3 |
| Cortado | Nacional | 42,1 |
| Importado | Importado | 36,7 |
| Cortado | Nacional | 40,5 |
| Rolado | Nacional | 38,9 |
| Importado | Importado | 37,2 |
| Rolado | Importado | 39,9 |
| Rolado | Nacional | 43,7 |
| Importado | Nacional | 41,4 |
| Rolado | Nacional | 41,0 |
| Cortado | Importado | 41,3 |
| Importado | Nacional | 41,3 |
| Importado | Importado | 36,7 |
| Rolado | Nacional | 40,1 |
| Cortado | Nacional | 41,3 |
| Rolado | Importado | 41,0 |
| Importado | Nacional | 40,6 |
| Cortado | Nacional | 40,4 |
| Rolado | Nacional | 40,3 |
| Importado | Nacional | 41,3 |
| Cortado | Importado | 40,1 |
| Rolado | Importado | 42,7 |
| Cortado | Importado | 41,6 |
| Importado | Nacional | 41,6 |
Cargaremos los datos en el sistema
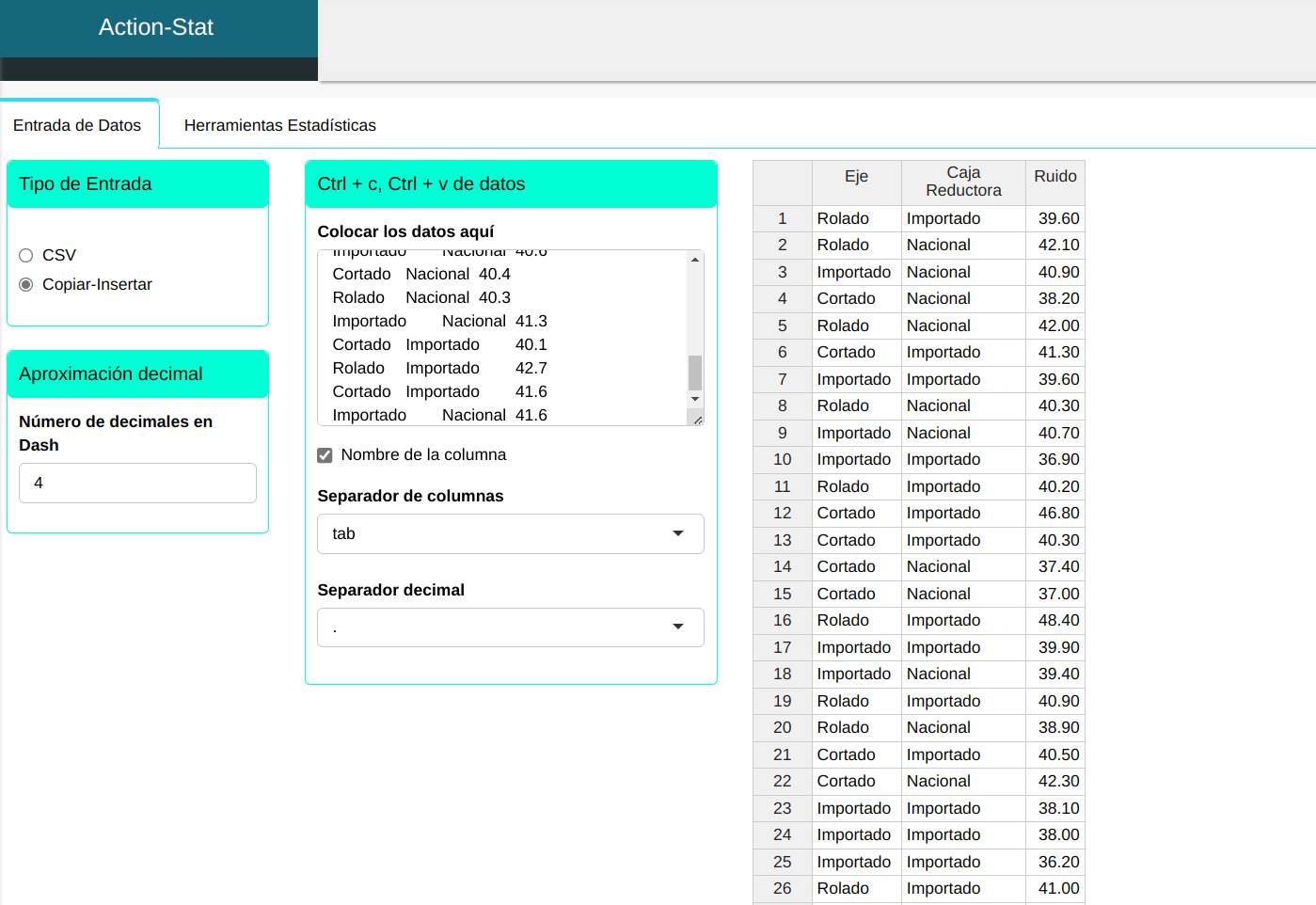
Se realizara la ANOVA efecto fijo
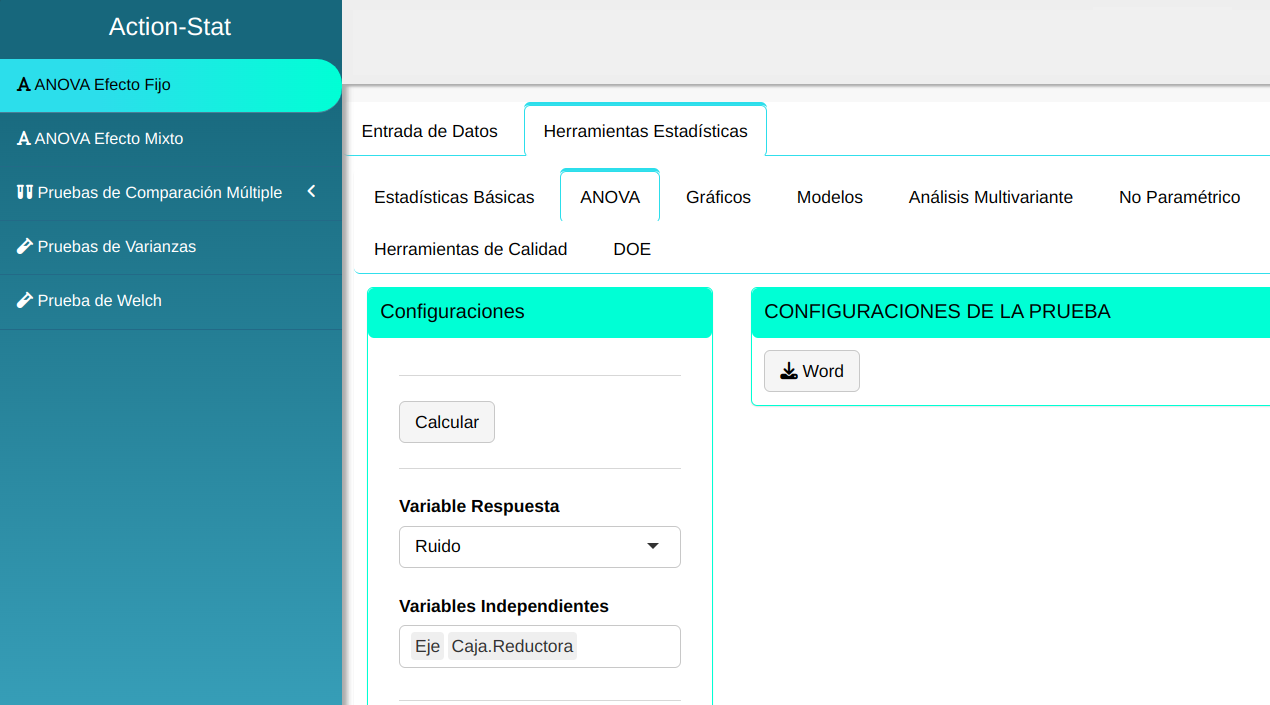
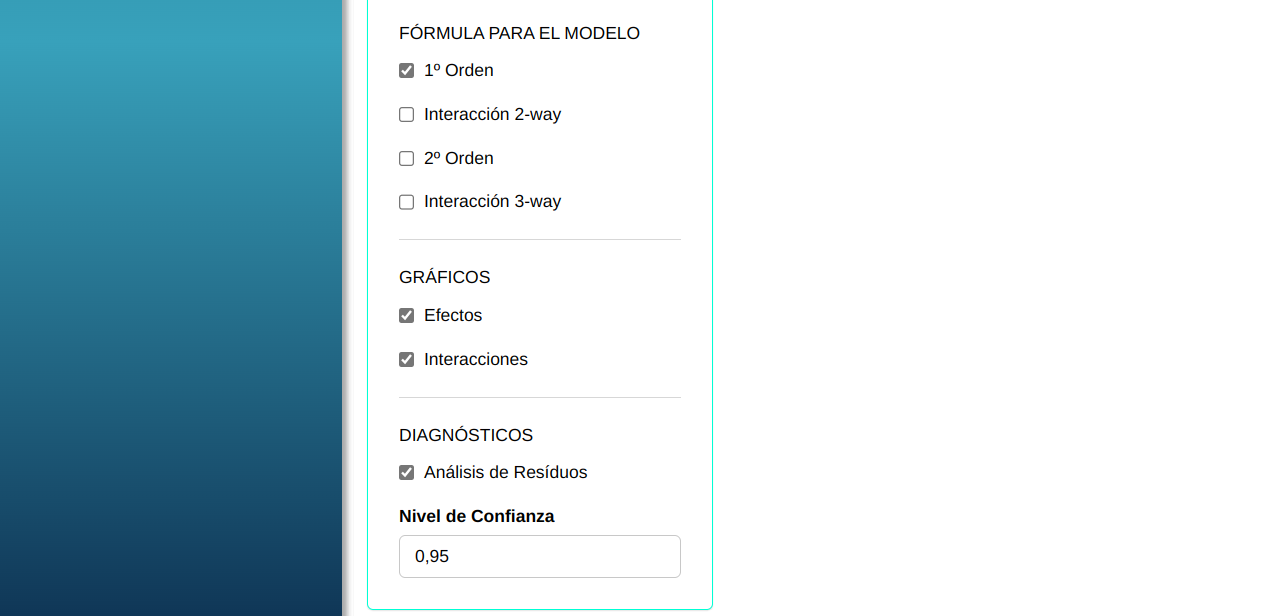
En seguida, haga un clic en calcular para obtener los resultados.

Los resultados son:
Cuadro de la ANOVA
| G.L. | Suma de Cuadrados | Cuadrado Medio | Estad. F | P-valor | |
|---|---|---|---|---|---|
| Eje | 2 | 32.667 | 16.334 | 3.644 | 0.033 |
| Caja.Reductora | 1 | 2.622 | 2.622 | 0.585 | 0.448 |
| Resíduos | 50 | 224.136 | 4.483 |
Intervalo de confianza de Efecto Eje
| Nivel | Límite Inferior | Efecto para media | Límite Superior |
|---|---|---|---|
| Cortado | 39.642 | 40.644 | 41.647 |
| Importado | 38.359 | 39.361 | 40.363 |
| Rolado | 40.220 | 41.222 | 42.225 |
Intervalo de confianza del Efecto Caja.Reductora
| Nível | Límite Inferior | Efecto para media | Límite Superior |
|---|---|---|---|
| Importado | 39.370 | 40.189 | 41.007 |
| Nacional | 39.811 | 40.630 | 41.448 |
Prueba de Normalidad
| Valor | |
|---|---|
| Media | 0.000 |
| Desviación Estándar | 2.056 |
| N | 54.000 |
| Anderson-Darling | 0.825 |
| P-Valor | 0.031 |
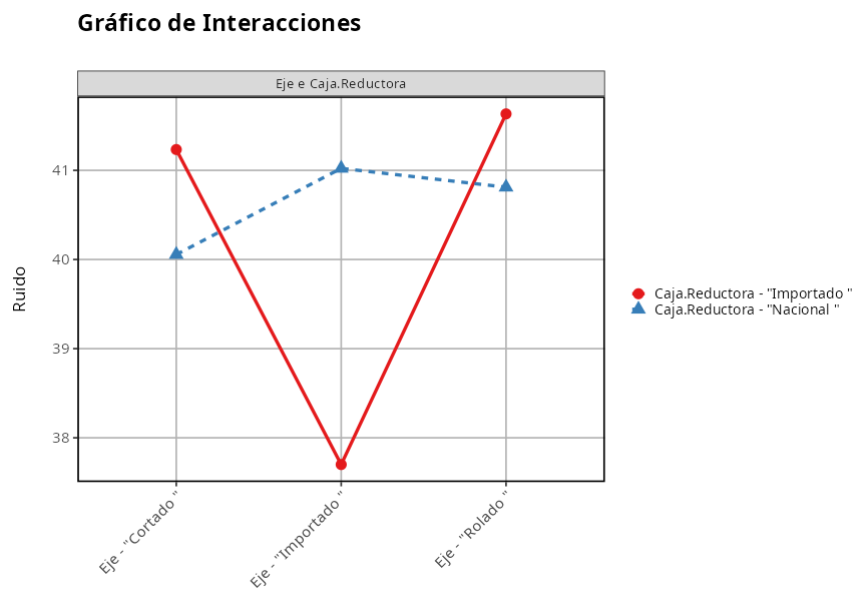
Como el valor P asociado con la interacción entre el eje y la caja de cambios es muy pequeño (0,00096), concluimos que la interacción entre estos factores es significativa. Por tanto, debemos tener cuidado al interpretar los factores.\
Para evaluar si existe interacción, simplemente debemos comprobar si la gráfica de los factores se cruza, como en la figura. Por tanto concluimos que existe una interacción entre los factores Caja Reductora y Eje.
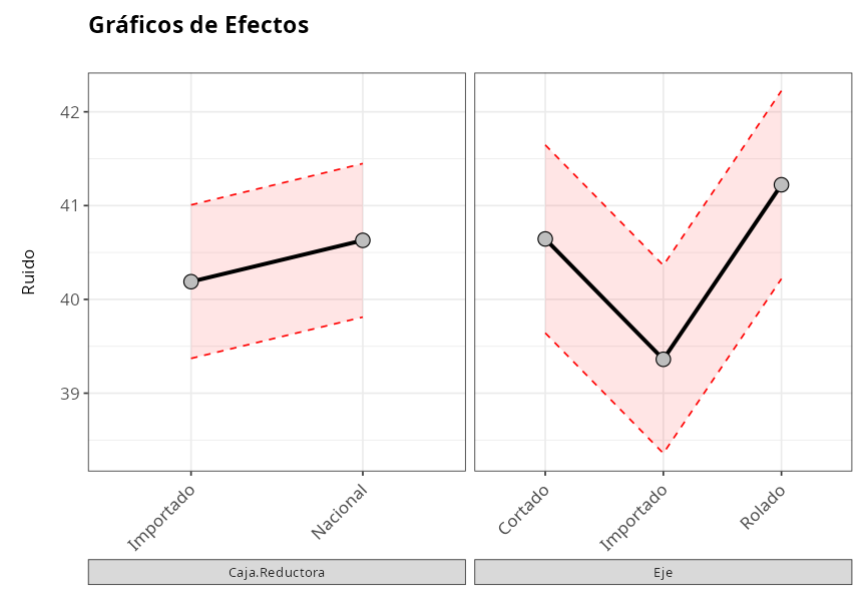
En el gráfico, los puntos negros son las medias de cada nivel de factor, que en la tabla se denominan Efectos. Las líneas rojas representan el intervalo de confianza de las medias de los niveles de los factores.
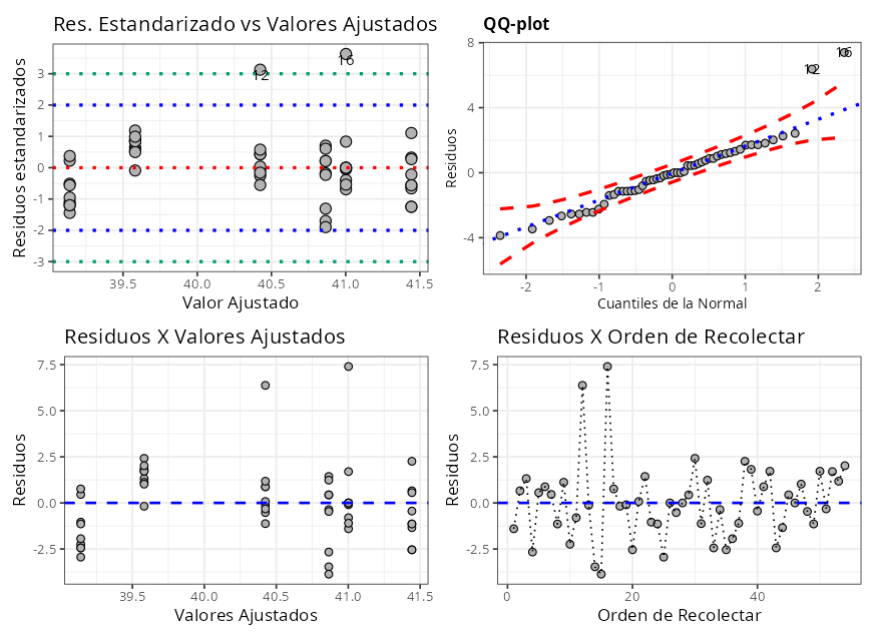
En el gráfico 1: Gráfico de Residuos Estandarizados versus Valores Ajustados.
En el gráfico 2: Gráfico de residuos versus cuantiles normales.
En el gráfico 3: Gráfico de Residuos versus Valores Ajustados.
En el gráfico 4: Gráfica de Residuos versus Orden de Recogida, con esta gráfica comprobamos si los residuos son independientes. El criterio para el análisis es: si los puntos de la gráfica se distribuyen aleatoriamente es indicativo de independencia, por otro lado, si presenta un patrón es indicativo de dependencia en los residuos. En nuestro caso, verificamos la independencia en los residuos.
En este caso usaremos la prueba de Anderson-Darling, donde la hipótesis nula es que los datos son normales, y a través del ejemplo verificamos que rechazamos la hipótesis nula y así verificar que los residuos no siguen una distribución normal.