1. ANOVA Efeito Fixo
A ANOVA é usada para analisar o comportamento de vários tratamentos de um fator aplicado ao processo e/ou produto.
Exemplo 1:
Considere um processo, produto ou serviço no qual queremos avaliar o impacto do fator A, tal que A tenha k níveis, sendo que esses níveis são fixos. Suponha que uma amostra de N unidades experimentais é selecionada completamente aleatória de uma população de unidades experimentais. A unidade experimental é a unidade básica para o qual os tratamentos são aplicados.
| Fator | Resistência |
|---|---|
| 15 | 7 |
| 15 | 7 |
| 15 | 15 |
| 15 | 11 |
| 15 | 9 |
| 20 | 12 |
| 20 | 17 |
| 20 | 12 |
| 20 | 18 |
| 20 | 18 |
| 25 | 14 |
| 25 | 18 |
| 25 | 18 |
| 25 | 19 |
| 25 | 19 |
| 30 | 19 |
| 30 | 25 |
| 30 | 22 |
| 30 | 19 |
| 30 | 23 |
| 35 | 7 |
| 35 | 10 |
| 35 | 11 |
| 35 | 15 |
| 35 | 11 |
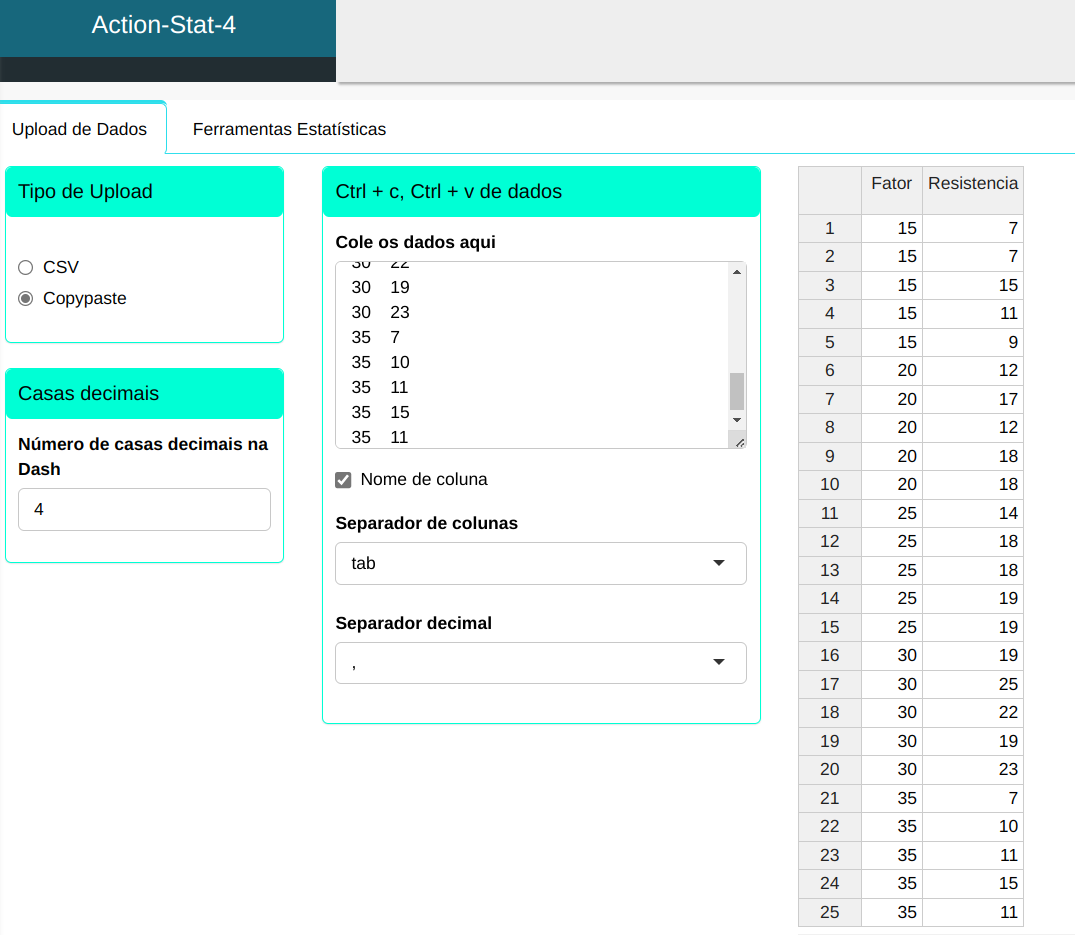
Realizaremos a ANOVA efeito fixo
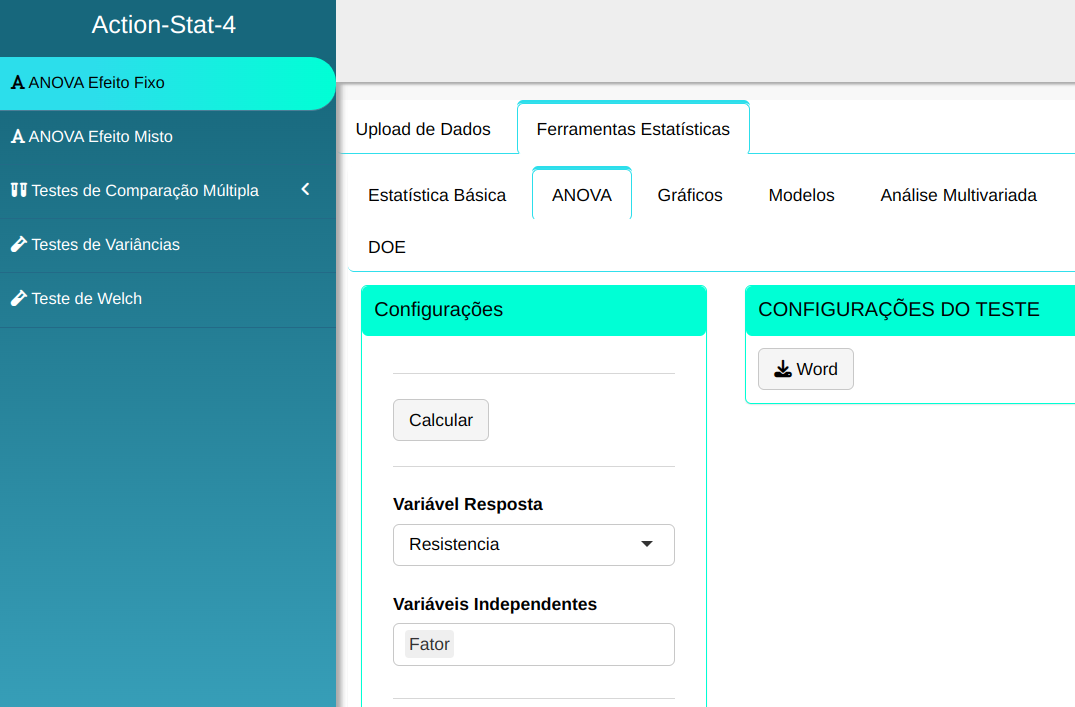
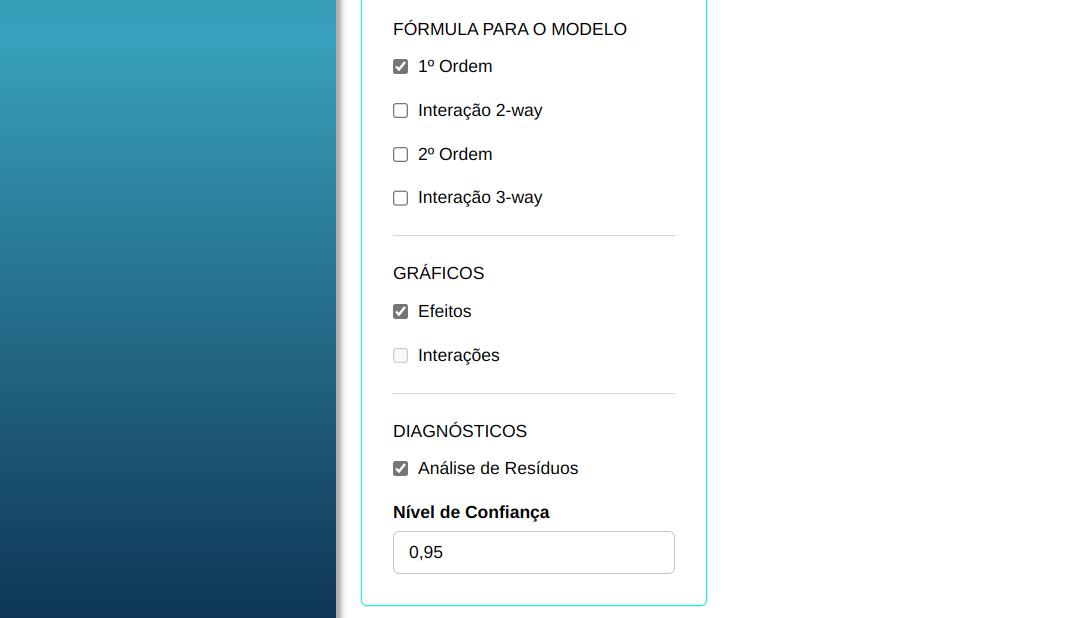
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Tabela da ANOVA
| G.L. | Soma de Quadrados | Quadrado Médio | Estat. F | P-valor | |
|---|---|---|---|---|---|
| Fator | 4 | 475.76 | 118.94 | 14.757 | 0 |
| Resíduos | 20 | 161.20 | 8.06 |
Intervalo de confiança do Efeito Fator
| Nível | Limite Inferior | Efeito para média | Limite Superior |
|---|---|---|---|
| 15 | 7.152 | 9.8 | 12.448 |
| 20 | 12.752 | 15.4 | 18.048 |
| 25 | 14.952 | 17.6 | 20.248 |
| 30 | 18.952 | 21.6 | 24.248 |
| 35 | 8.152 | 10.8 | 13.448 |
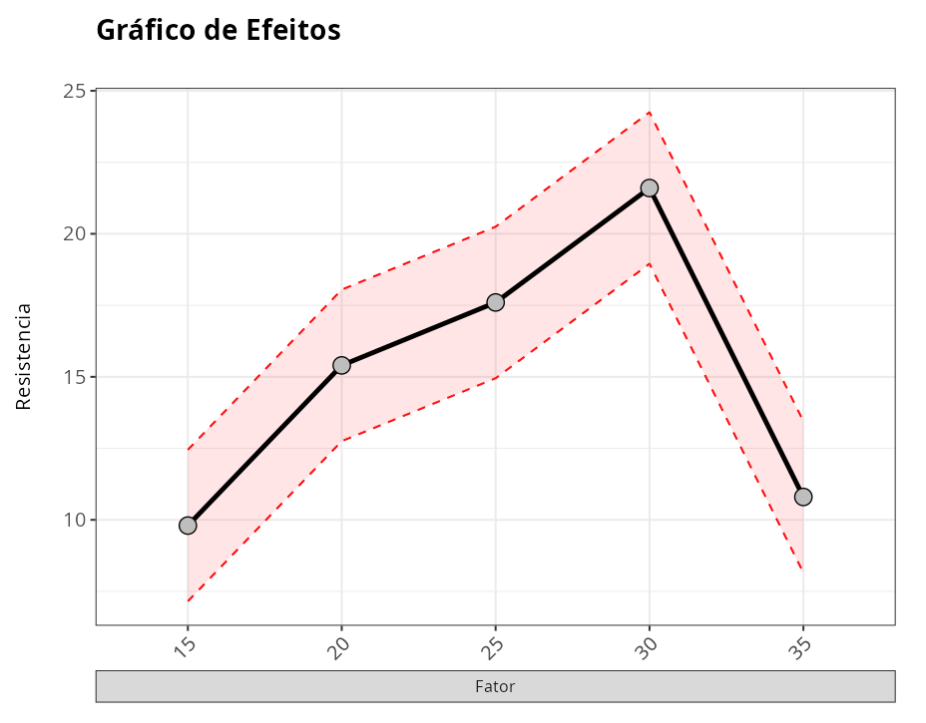
Testes de Normalidade
| Valor | |
|---|---|
| Média | 0 |
| Desvio Padrão | 2.592 |
| N | 25 |
| Anderson-Darling | 0.519 |
| P-Valor | 0.170 |
Neste exemplo temos que a Soma de Quadrados do Fator (475,76) é bem maior que a Soma de Quadrados do Erro (161,20) o que já é indício de que as médias não são iguais.
Se o P-valor for menor ou igual ao nível de significância ($\alpha$) pré-determinado, isto significa que as médias dos níveis são diferentes. Caso contrário, serão iguais. Neste caso, como ele é menor que 0,05, rejeitamos a hipótese nula de igualdade dessas médias, ou seja, podemos dizer que as médias dos níveis são diferentes.
No gráfico de efeitos, os pontos pretos, são as médias de cada nível do fator, que na tabela são denominados Efeitos.
As linhas vermelhas representam o intervalo de confiança para as médias dos níveis do fator.
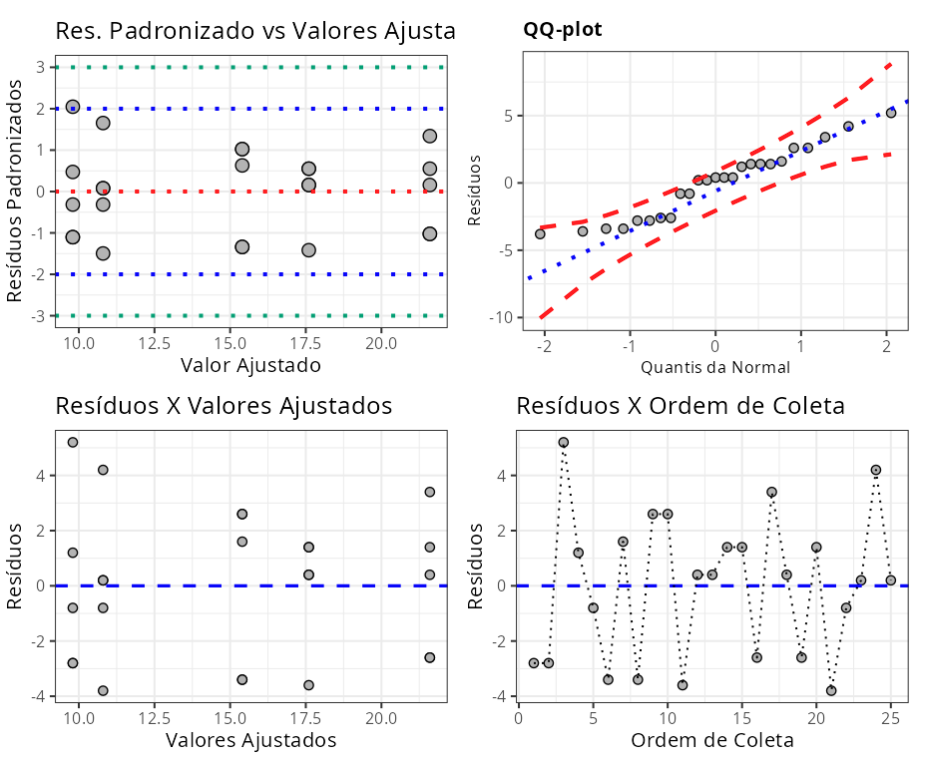
No gráfico 1: Gráfico de Resíduos Padronizados versus Valores Ajustados.
No gráfico 2: Gráfico de Resíduos versus Quantis da Normal.
No gráfico 3: Gráfico de Resíduos versus Valores Ajustados.
No gráfico 4: Gráfico de Resíduos versus Ordem de Coleta, com esse gráfico verificamos se os resíduos são independentes. O critério para a análise é: se os pontos do gráfico estiverem distribuídos de forma aleatória, é um indicativo de independência, por outro lado, se apresentarem um padrão é indicativo de dependência nos resíduos. No nosso caso, verificamos independência nos resíduos.
$\quad$ No nosso caso, usaremos o teste de Anderson-Darling, onde a hipótese nula é de a normalidade dos dados, e pelo exemplo, verificamos a não rejeição ("aceitação") a hipótese nula e com isso verificamos a normalidade dos resíduos.
Exemplo 2:
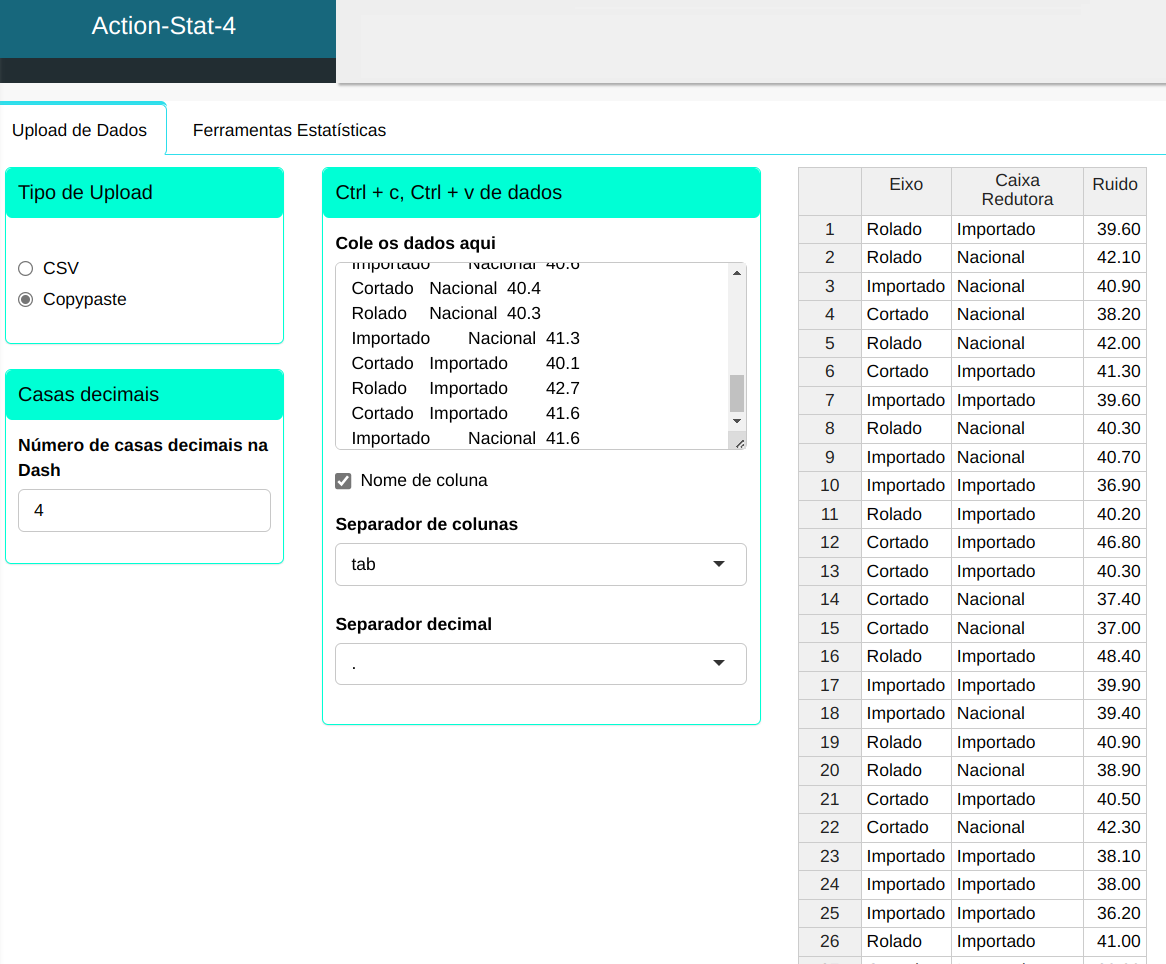
Uma empresa que produz limpadores de para-brisa para automóveis quer saber como os fatores Tipo de Caixa Redutora e Tipo de Eixo, utilizados na fabricação dos motores que acionam os limpadores, influenciam o ruído produzido, quando da utilização destes. Para isso realizamos um experimento com 54 motores, com 3 tipos de Eixo (Rolado, Cortado e Importado) e 2 tipos de Caixas Redutora (Nacional e Importada). Para cada motor (unidade experimental) medimos o ruído. Os dados estão na tabela seguinte.
| Eixo | Caixa Redutora | Ruido |
|---|---|---|
| Rolado | Importado | 39,6 |
| Rolado | Nacional | 42,1 |
| Importado | Nacional | 40,9 |
| Cortado | Nacional | 38,2 |
| Rolado | Nacional | 42 |
| Cortado | Importado | 41,3 |
| Importado | Importado | 39,6 |
| Rolado | Nacional | 40,3 |
| Importado | Nacional | 40,7 |
| Importado | Importado | 36,9 |
| Rolado | Importado | 40,2 |
| Cortado | Importado | 46,8 |
| Cortado | Importado | 40,3 |
| Cortado | Nacional | 37,4 |
| Cortado | Nacional | 37 |
| Rolado | Importado | 48,4 |
| Importado | Importado | 39,9 |
| Importado | Nacional | 39,4 |
| Rolado | Importado | 40,9 |
| Rolado | Nacional | 38,9 |
| Cortado | Importado | 40,5 |
| Cortado | Nacional | 42,3 |
| Importado | Importado | 38,1 |
| Importado | Importado | 38 |
| Importado | Importado | 36,2 |
| Rolado | Importado | 41 |
| Cortado | Importado | 39,9 |
| Rolado | Importado | 41 |
| Cortado | Nacional | 41,3 |
| Importado | Nacional | 42 |
| Cortado | Importado | 39,3 |
| Cortado | Nacional | 42,1 |
| Importado | Importado | 36,7 |
| Cortado | Nacional | 40,5 |
| Rolado | Nacional | 38,9 |
| Importado | Importado | 37,2 |
| Rolado | Importado | 39,9 |
| Rolado | Nacional | 43,7 |
| Importado | Nacional | 41,4 |
| Rolado | Nacional | 41 |
| Cortado | Importado | 41,3 |
| Importado | Nacional | 41,3 |
| Importado | Importado | 36,7 |
| Rolado | Nacional | 40,1 |
| Cortado | Nacional | 41,3 |
| Rolado | Importado | 41 |
| Importado | Nacional | 40,6 |
| Cortado | Nacional | 40,4 |
| Rolado | Nacional | 40,3 |
| Importado | Nacional | 41,3 |
| Cortado | Importado | 40,1 |
| Rolado | Importado | 42,7 |
| Cortado | Importado | 41,6 |
| Importado | Nacional | 41,6 |
Faremos o upload dos dados no sistema.
Realizaremos a ANOVA efeito fixo
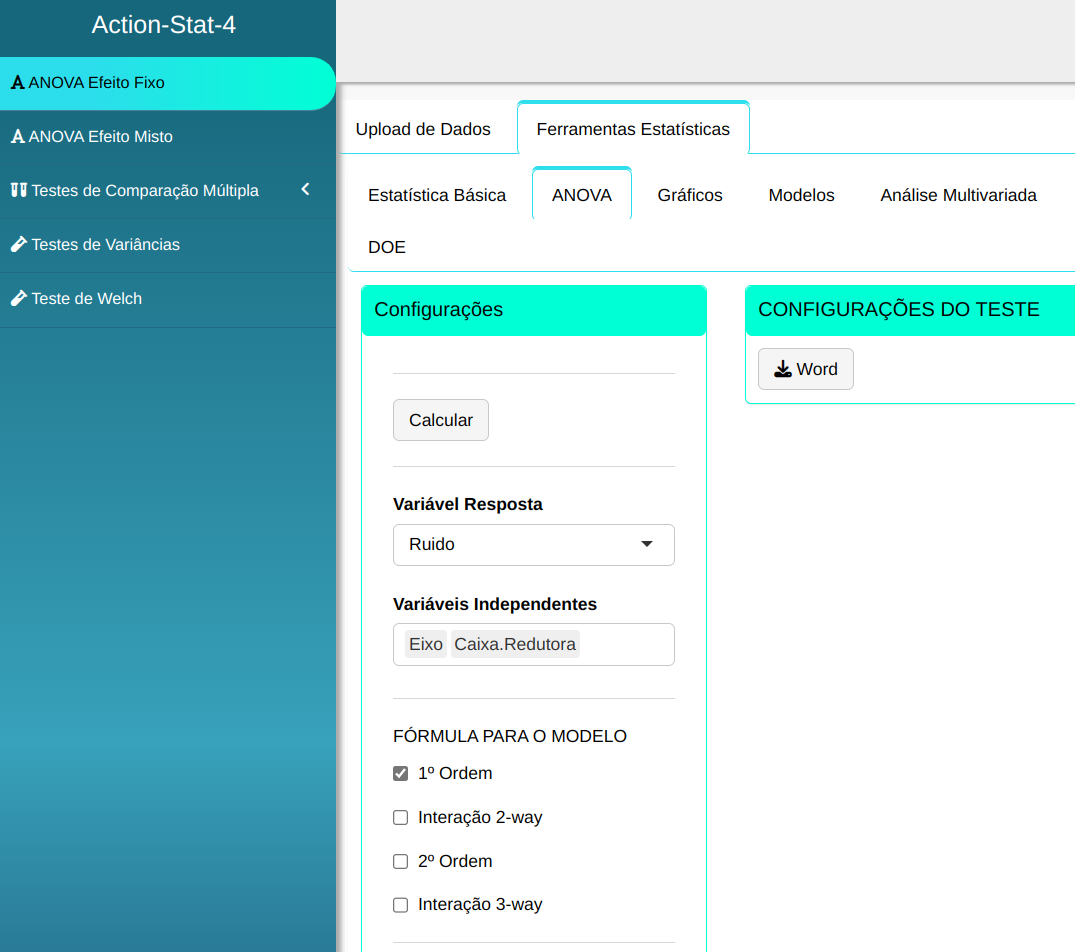
Em seguida, clique em Calcular para obter os resultados. Também é possível gerar as análises e descarregá-las em formato Word.

Os resultados são:
Tabela da ANOVA
| G.L. | Soma de Quadrados | Quadrado Médio | Estat. F | P-valor | |
|---|---|---|---|---|---|
| Eixo | 2 | 32.667 | 16.334 | 3.644 | 0.033 |
| Caixa.Redutora | 1 | 2.622 | 2.622 | 0.585 | 0.448 |
| Resíduos | 50 | 224.136 | 4.483 |
Intervalo de confiança do Efeito Eixo
| Nível | Limite Inferior | Efeito para média | Limite Superior |
|---|---|---|---|
| Cortado | 39.642 | 40.644 | 41.647 |
| Importado | 38.359 | 39.361 | 40.363 |
| Rolado | 40.220 | 41.222 | 42.225 |
Intervalo de confiança do Efeito Caixa.Redutora
| Nível | Limite Inferior | Efeito para média | Limite Superior |
|---|---|---|---|
| Importado | 39.370 | 40.189 | 41.007 |
| Nacional | 39.811 | 40.630 | 41.448 |
Testes de Normalidade
| Valor | |
|---|---|
| Média | 0 |
| Desvio Padrão | 2.056 |
| N | 54 |
| Anderson-Darling | 0.825 |
| P-Valor | 0.031 |
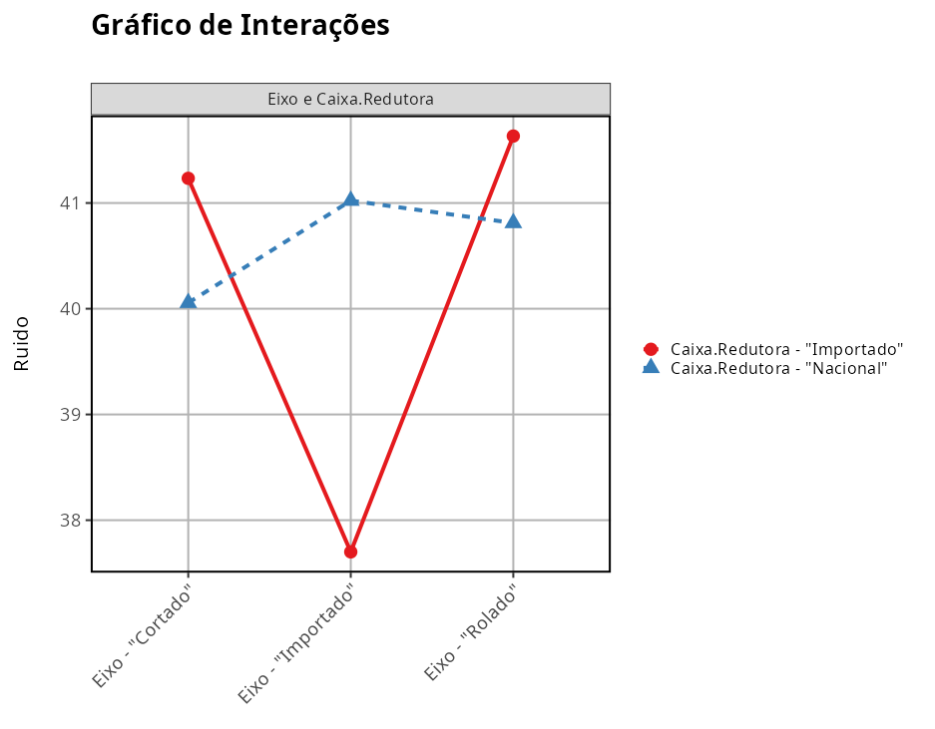
Como o P-valor associado a interação entre o eixo e a caixa redutora é muito pequeno (0,00096) concluímos que a interação entre estes fatores é
significativa. Desta forma, temos que ter cuidado na interpretação do fatores.
Para avaliarmos se existe interação, basta verificarmos se o gráfico dos fatores se interceptam, como na figura. Concluímos então que existe interação entre os fatores Caixa Redutora e Eixo.
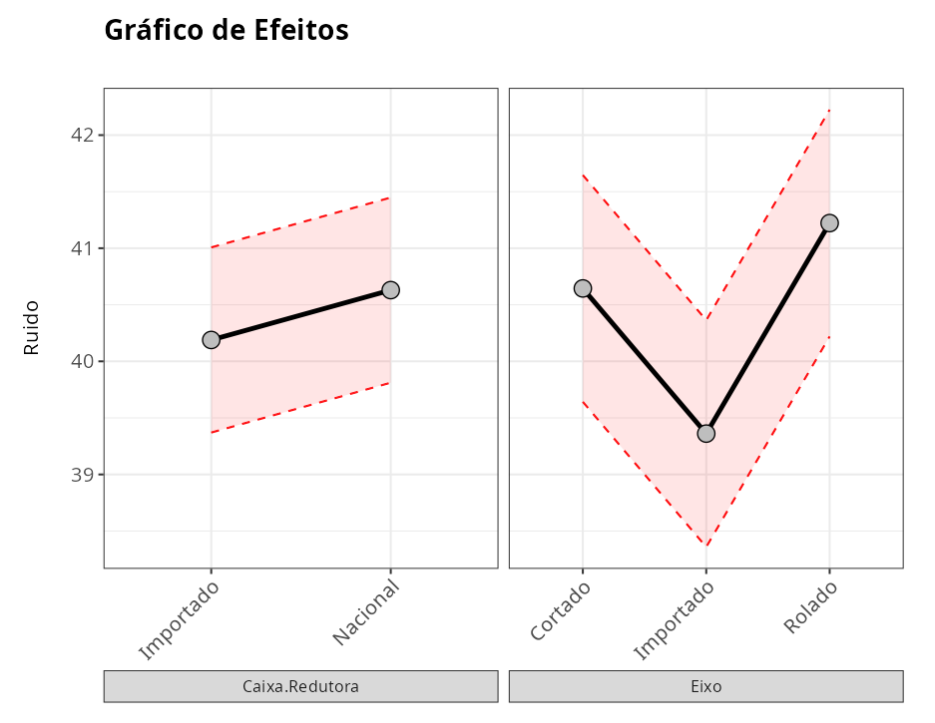
No gráfico, os pontos pretos, são as médias de cada nível do fator, que na tabela são denominados Efeitos. As linhas vermelhas representam o intervalo de confiança para as médias dos níveis do fator.
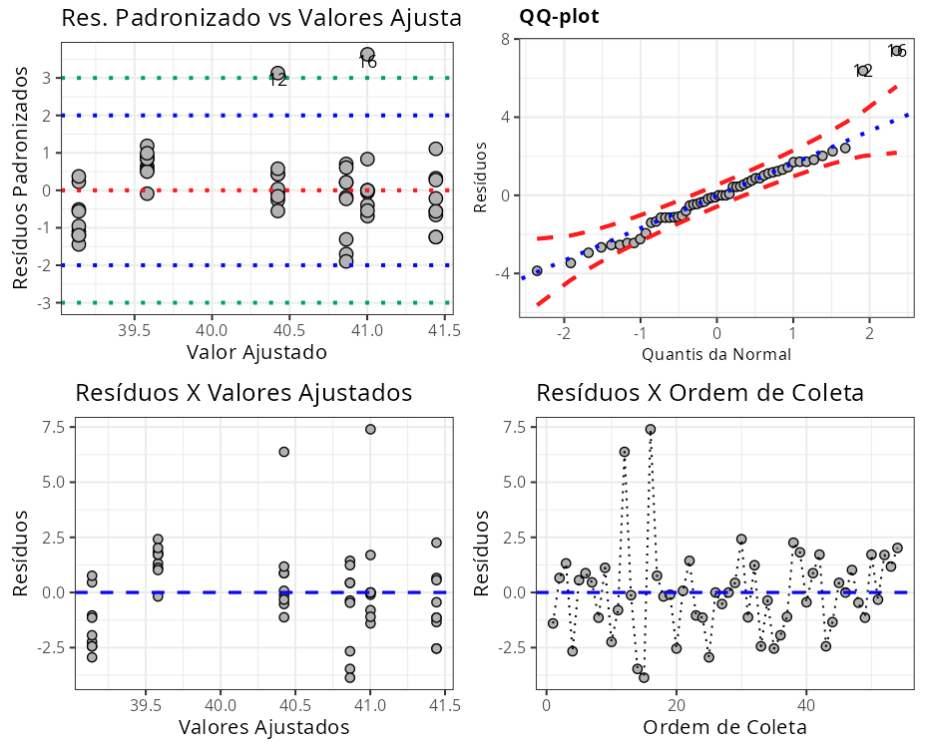
No gráfico 1: Gráfico de Resíduos Padronizados versus Valores Ajustados.
No gráfico 2: Gráfico de Resíduos versus Quantis da Normal.
No gráfico 3: Gráfico de Resíduos versus Valores Ajustados.
No gráfico 4: Gráfico de Resíduos versus Ordem de Coleta, com esse gráfico verificamos se os resíduos são independentes. O critério para a análise é: se os pontos do gráfico estiverem distribuídos de forma aleatória, é um indicativo de independência, por outro lado, se apresentarem um padrão é indicativo de dependência nos resíduos. No nosso caso, verificamos independência nos resíduos.
Neste caso, usaremos o teste de Anderson-Darling, onde a hipótese nula é de a normalidade dos dados, e pelo exemplo, verificamos que rejeitamos a hipótese nula e com isso verificamos que os resíduos não seguem distribuição normal.